GF域上的RSA学习笔记
0x01 学习背景
之前我们提到了RSA在整数运算中的加密和 解密方式,今天我们来讨论讨论RSA在$GF(2^m)$域中的计算方法和解题模式。与以前的$RSA$略有不同
0x02 GF域中多项式的运算
0o01GF域的概念(个人总结的)
设$p$为质数,那么当且仅当$m=p^k$时,$GF(m)$才有意义。例如:$GF(11),GF(81),GF(256),GF(7^{20011230})$均为有意义的GF域。然而,$GF(12)$不是有意义的$GF$域,因为$12=2^2×3$,不能写成$p^k$的形式 。
0o02 多项式在$GF(p^k)$域中的形式
设$f(x)$是关于$x$的一个多项式。那么在$GF(P^k)$中,$f(x)$的次数为$k$,并且$f(x)$的每一项系数均小于$p$,因为$f(x)$都是要对$p$取模的。
对多项式取整数模的方法很简单:每一项系数对取那个整数取模,例如:$x^5+5x^4+10x^3+10x^2+5x+1 \equiv x^5+5x^4+x^3+x^2+5x+1 \mod 9$,$12x^3+15x^2-x+8\equiv 4x^3+7x^2+7x \mod 8$
例如:在$GF(2^k)$域中。设$f(x)=x+1$,那么$f^2(x)=x^2+2x+1\equiv x^2+1 \mod 2$。
当然,在$GF(p^k)$域中,$Z_{p^k}$中的每一个整数都与对应的多项式一一对应。例如:在$GF(2^8)$中,$1$化为多项式为$1$,$2$化为多项式为$x$,$3$化为多项式为$x+1$,$13$化为多项式为$x^3+x^2+1$。也就是说,我们把对应的数化为$2$进制,然后从最低位为$0$次项一项一项地确定那一次的系数。
所以,在$GF(2^k)$域中,有$3^2=5$也就不足为奇了,这也就说明:虽然多项式可以表示为整数,但是多项式的运算与整数运算是不一样的!
0o03 什么叫做不可约多项式
不可约多项式可以理解为质数,也就是说:除了$1$和它本身,不可以被分解成几个因数之积的形式。例如:在$GF(2^8)$中,$x^8+x^4+x^3+x+1$就是一个不可约多项式(注意:最高项系数一定非$0$并且次数恰好为$p^k$中$k$的值。
当然,在$GF(2^8)$中,$x^3+x^2+x+1$就不是一个不可约多项式,因为它可以分解因式为$(x+1)^3$
0x03 解题步骤
1.此类题目一般给出了$n(x),e$和$c$。不过我们得到$c$的值之后要将其化为$c(x)$的表达式。
2.然后,我们尝试分解$n(x)$,这一步在Sagemath的Notebook下面很容易做到。
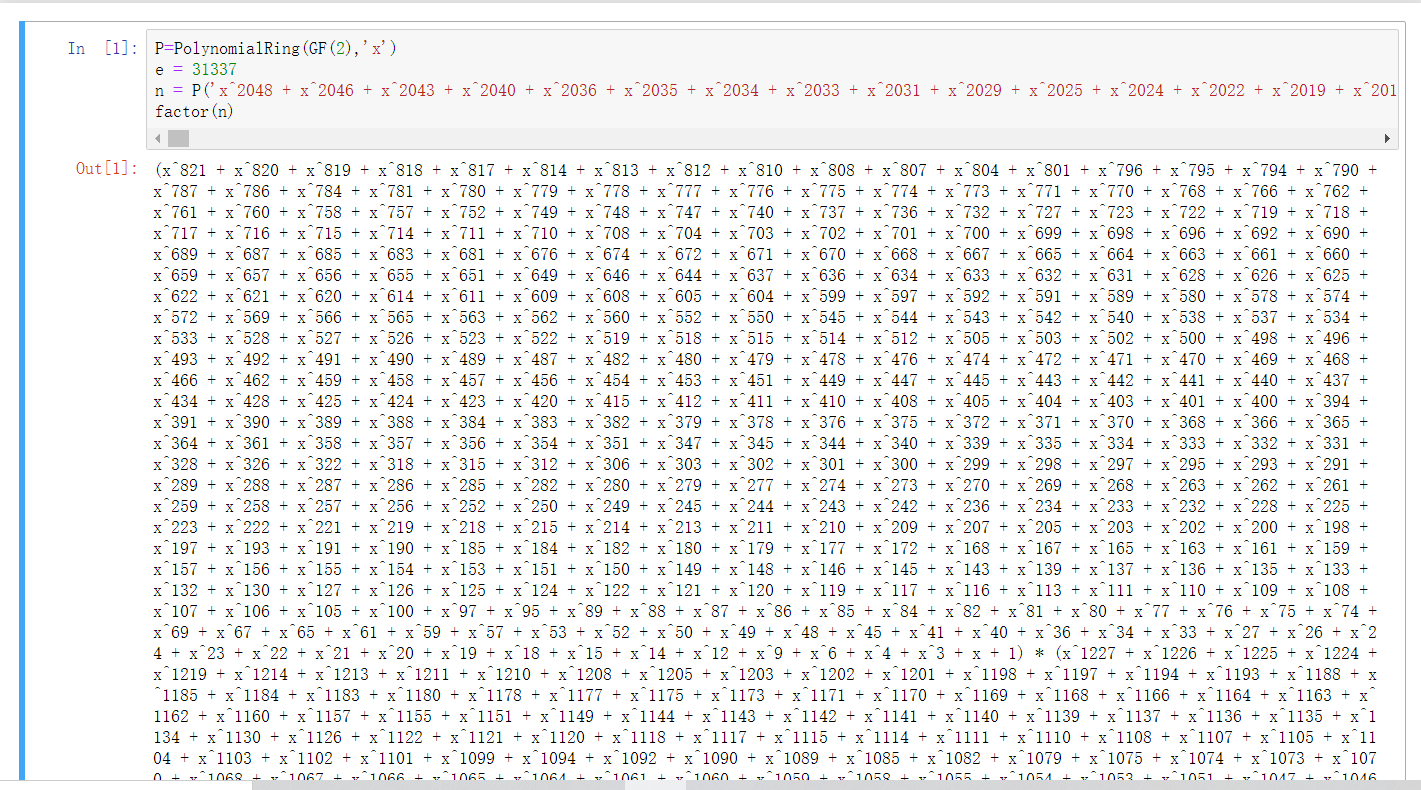
值得注意的是,我们这里分解到的是两个不可约多项式$p(x)$和$q(x)$,显然,这是两个多项式而不是数字。我们该如何计算$\phi$值呢?
以前当$p,q$均为质数的时候,$\phi(p)=(p-1),\phi(q)=(q-1) $。我们回归一下$\phi(A)$的定义:在$Z_A$与$A$互质的数字个数。所以,在$GF(2^k)$中,由于除了这个多项式自己之外,其他一共$2^{k}-1$个多项式都与这个不q可约多项式互质,所以在这里,由于$p(x)$的最高次项为$821$,那么$\phi[p(x)]=2^{821}-1$。同理,$\phi[q(x)]=2^{1227}-1$,故这里的$\phi[n(x)]=\phi[p(x)]\phi[q(x)]$
下一步,我们可以计算$d$的值,这里贴一下Sagemath中的代码

在求出$d$的时候,我们就可以计算$c^d(x) \mod n(x)$的多项式$m(x)$

把运行结果复制到一个TXT文档中(例如1.txt或者1.in),然后化成二进制数(C++脚本很好打的,不过本fw怕忘掉怎么打这个C++脚本还是把脚本贴了上来)
多项式转二进制数的脚本(多项式中加号与每一项之间存在空格,所以直接判断长度是否≥$3$即可)
1 |
|
二进制数转多项式的脚本(注意删去最后的加号)
1 |
|
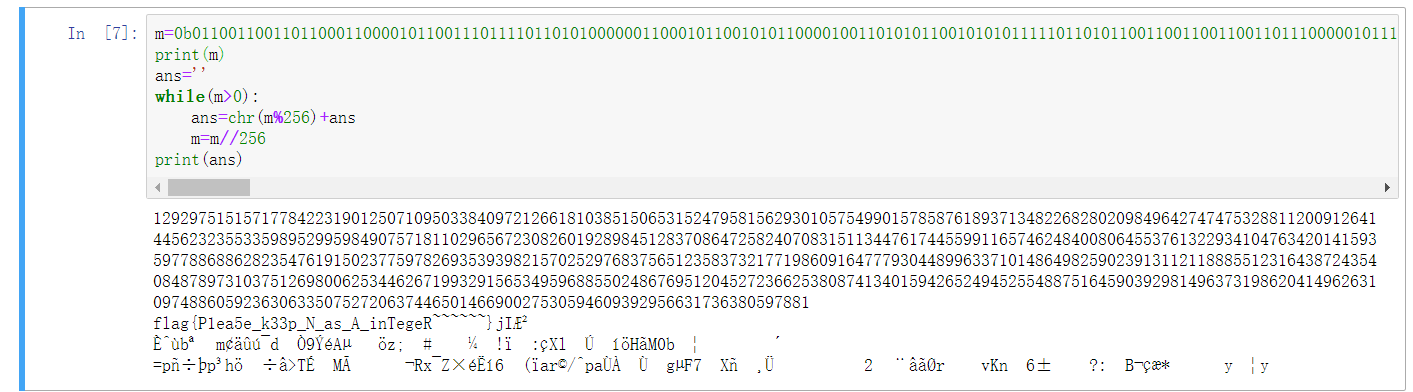
最后,我们把$m(x)$化为它所对应的数值,然后将其转化为字符串就可以得到答案了