21Jan1

huangx607087寒假的切题1

0x00 简介

一个密码学废物的寒假切题记录的exp，别看，贼菜

近期BUUCTF的分数上到了500分，不过目前的形式依然很严峻，与我同级的一个人比我强很多，而我却在这里补基础，感觉校队里同一级除web方向的人不可同时存在2个及以上，压力还是非常大的

#define huangx607087 yongyuandefeiwu

0x01 ECC & RSA

这是一道结合了离散对数和椭圆曲线的密码体系，我们可以先看一下加密代码和题目所给出的的各种数据。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
from fastecdsa.curve import P521 as Curve
from fastecdsa.point import Point
from Crypto.Util.number import bytes_to_long, isPrime
from os import urandom
from random import getrandbits
def gen_rsa_primes(G):
	urand = bytes_to_long(urandom(521//8))
	while True:
		s = getrandbits(521) ^ urand
		Q = s*G
		if isPrime(Q.x) and isPrime(Q.y):
			print("ECC Private key:", hex(s))
			print("RSA primes:", hex(Q.x), hex(Q.y))
			print("Modulo:", hex(Q.x * Q.y))
			return (Q.x, Q.y)
flag = int.from_bytes(input(), byteorder="big")
ecc_p = Curve.p
a = Curve.a
b = Curve.b
Gx = Curve.gx
Gy = Curve.gy
G = Point(Gx, Gy, curve=Curve)
e = 0x10001
p, q = gen_rsa_primes(G)
n = p*q
file_out = open("downloads/ecc-rsa.txt", "w")
file_out.write("ECC Curve Prime: " + hex(ecc_p) + "\n")
file_out.write("Curve a: " + hex(a) + "\n")
file_out.write("Curve b: " + hex(b) + "\n")
file_out.write("Gx: " + hex(Gx) + "\n")
file_out.write("Gy: " + hex(Gy) + "\n")
file_out.write("e: " + hex(e) + "\n")
file_out.write("p * q: " + hex(n) + "\n")
c = pow(flag, e, n)
file_out.write("ciphertext: " + hex(c) + "\n")
'''
ECC Curve Prime: 0x1ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
Curve a: -0x3
Curve b: 0x51953eb9618e1c9a1f929a21a0b68540eea2da725b99b315f3b8b489918ef109e156193951ec7e937b1652c0bd3bb1bf073573df883d2c34f1ef451fd46b503f00
Gx: 0xc6858e06b70404e9cd9e3ecb662395b4429c648139053fb521f828af606b4d3dbaa14b5e77efe75928fe1dc127a2ffa8de3348b3c1856a429bf97e7e31c2e5bd66
Gy: 0x11839296a789a3bc0045c8a5fb42c7d1bd998f54449579b446817afbd17273e662c97ee72995ef42640c550b9013fad0761353c7086a272c24088be94769fd16650
e: 0x10001
p * q: 0x118aaa1add80bdd0a1788b375e6b04426c50bb3f9cae0b173b382e3723fc858ce7932fb499cd92f5f675d4a2b05d2c575fc685f6cf08a490d6c6a8a6741e8be4572adfcba233da791ccc0aee033677b72788d57004a776909f6d699a0164af514728431b5aed704b289719f09d591f5c1f9d2ed36a58448a9d57567bd232702e9b28f
ciphertext: 0x3862c872480bdd067c0c68cfee4527a063166620c97cca4c99baff6eb0cf5d42421b8f8d8300df5f8c7663adb5d21b47c8cb4ca5aab892006d7d44a1c5b5f5242d88c6e325064adf9b969c7dfc52a034495fe67b5424e1678ca4332d59225855b7a9cb42db2b1db95a90ab6834395397e305078c5baff78c4b7252d7966365afed9e
'''

我们通过上面的加密过程可以发现：$(p,q)$实际上是椭圆曲线$y^2=x^3+ax+b$上面的点，所以我们可以有一个等式为$q^2=p^3+ap+b$，加上RSA中的等式$n=pq$，两边平方后带入$q^2$表达式为$n^2=p^5+ap^3+bp^2$，然后用以下的sagemath代码即可，注意求解多项式的根应该是$f=0$的根，所以最后要减去一个$n^2$，把方程化成$p^5+ap^3+bp^2-n^2=0$

1-1

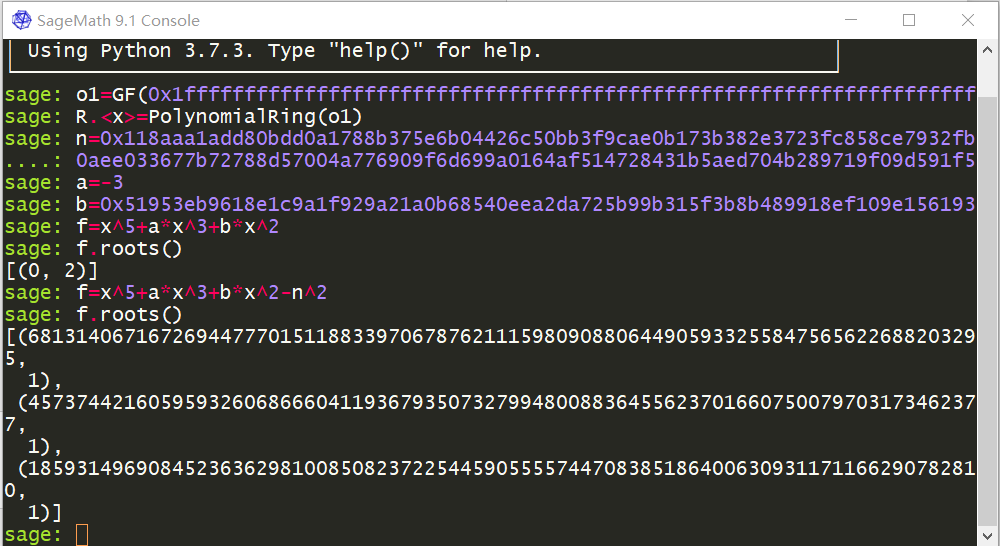
最后求出来$3$个解，很显然，由于RSA中$p$是素数，那么只有第二个解符合题意。此时$n$就被分解成功，进而我们就很快地能够解密了。

下面附上一些Sagemath中对密码学有关的函数供以后查阅

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
#整数域,有理数域和实数域
ZZ(3)
QQ(0.25)
RR(2^0.5)
#复数域
CC(1,2)
#生成虚数单位i
i=ComplexField().gen();(2+i)*(4+3*i)
#构造多项式环,返回具有给定属性和变量名的全局唯一的单变量或多元多项式环
#定义在整数域上的多项式环R，变量为w;ZZ也可换成其他数域
R.<w>=PolynomialRing(ZZ);R
(1 + w)^3
#有限环
RN=IntegerModRing(63)
FR=Integers(17);FR
#自身的代数扩展;exR=FR[w]/(w^2+3)
exR=FR.extension(w^2+3)；exR
#以python整数的形式返回所有可逆元素的列表
FR.list_of_elements_of_multiplicative_group()
#假设环的乘法群是循环的，返回这个环的乘法群的生成元
FR.multiplicative_generator()
#返回这个环的一个随机元素
FR.random_element()
#上述几种方法对如下的域同样支持
#有限域
#素数域
G1=GF(37);G1
#伽罗瓦域
G2=GF(3^5);G2
#同时求商与余数
q,r=divmod(12,5)
#求公约数
d=gcd(12,5)
#扩展的欧几里得算法
d,u,v=xgcd(12,5)
#12在模5下的逆
u=inverse_mod(12,5)
#生成[lb,ub)之间的随机素数,注意ub在前,lb在后,lb可缺省为0
#可通过这种方式生成128位的随机素数
p=random_prime(2L**128,2L**127)
#判断是否为素数
is_prime(65537)
#第20个素数
nth_prime(20)
#计算x^y mod n
z=power_mod(12,5,17)
#欧拉函数
euler_phi(111)
#中国剩余定理,A=[a1,...,an],M=[m1,...,mn]
#ai=x mod mi,i=1,...,n
crt([1,2,3,4],[7,5,12,23])
#求自身的n次根
FR(12).nth_root(7,all='True')
#求多项式的根，roots方法必须作用在域上
R.<x>=PolynomialRing(G1)
xt=G1(12)
yt=xt^6
f=x^6-yt
f.roots()
#定义矩阵，默认定义在实数域
A = matrix([[1,2,3,5],[3,2,1,2],[1,1,1,0],[3,7,2,2]])
A^-1
#定义在其他域上的矩阵，如有限域
A = matrix(GF(13),[[1,2,3,5],[3,2,1,2],[1,1,1,0],[3,7,2,2]])
A^-1
#可以看到两个逆矩阵不一样
#定义向量，定义在有限域，默认定义在实数域
w = vector(GF(13),[1,1,4,3])
Y=A*w;Y
Z=w*A;Z
#解线性方程组AX=Y
X = A.solve_right(Y);X
#也可以使用符号\
A\Y
#解线性方程组XA=Y
X = A.solve_left(Z);X
#格基约减
A = matrix([[1,2,3,5],[3,2,1,2],[1,1,1,0],[3,7,2,2]])
#LLL算法
A.LLL()
#BKZ算法
A.BKZ()
p=ZZ('FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF',16)
a=ZZ('FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC',16)
b=ZZ('28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93',16)
#有限域GF(p)上的椭圆曲线y^2 = x^3 + a*x + b mod p
E=EllipticCurve(GF(p),[0,0,0,a,b])
#基点
g=E([ZZ('32c4ae2c1f1981195f9904466a39c9948fe30bbff2660be1715a4589334c74c7',16),ZZ('bc3736a2f4f6779c59bdcee36b692153d0a9877cc62a474002df32e52139f0a0',16)])
#基点的阶
n=ZZ('FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123',16)
#生成密钥
sk=random_prime(2*n//3,n//3)
#生成公钥
G=sk*g
#通用的求离散对数的方法
x=discrete_log(a,base,ord,operation)
#求离散对数的Pollard-Rho算法
x=discrete_log_rho(a,base,ord,operation)
#求离散对数的Pollard-kangaroo算法(也称为lambda算法)
x=discrete_log_lambda(a,base,bounds,operation)
#小步大步法
x=bsgs(base,a,bounds,operation)

2.[*ctf]little case&[NCTF2019]easyRSA

这两道题都是涉及到了RSA中$\gcd(p-1,q-1,e)=e$的情况，直接查阅RSA Notes 3中的相关内容即可，此处不再赘述。

3.[NPUCTF2020]Mersenne twister

一道梅森旋转题，还是先看一下题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
from hashlib import *
from itertools import *
from binascii import hexlify , unhexlify
from flag import flag ,seed
assert len(flag) == 26
assert flag[:7] == 'npuctf{'
assert flag[-1] == '}'
XOR = lambda s1 ,s2 : bytes([x1 ^ x2 for x1 ,x2 in zip(s1 , s2)])
class mt73991:
    def __init__(self , seed):
        self.state = [seed] + [0] * 232
        self.flag = 0
        self.srand()
        self.generate()
    def srand(self):
        for i in range(232):
            self.state[i+1] = 1812433253 * (self.state[i] ^ (self.state[i] >> 27)) - i
            self.state[i+1] &= 0xffffffff
    def generate(self):
        for i in range(233):
            y = (self.state[i] & 0x80000000) | (self.state[(i+1)%233] & 0x7fffffff)
            temp = y >> 1
            temp ^= self.state[(i + 130) % 233]
            if y & 1:
                temp ^= 0x9908f23f
            self.state[i] = temp
    def getramdanbits(self):
        if self.flag == 233:
            self.generate()
            self.flag = 0
        bits = self.Next(self.state[self.flag]).to_bytes(4 , 'big')
        self.flag += 1
        return bits    
    def Next(self , tmp):
        tmp ^= (tmp >> 11)
        tmp ^= (tmp << 7) & 0x9ddf4680
        tmp ^= (tmp << 15) & 0xefc65400
        tmp ^= (tmp >> 18) & 0x34adf670
        return tmp
def encrypt(key , plain):
    tmp = md5(plain).digest()
    return hexlify(XOR(tmp , key))
if __name__ == "__main__":
    flag = flag.encode()
    random = mt73991(seed)
    f = open('./cipher.txt' , 'wb')
    for i in flag:
        key = b''.join([random.getramdanbits() for _ in range(4)])
        cipher = encrypt(key , chr(i).encode())
        f.write(cipher)

这道题目与之前我博客里的**PRNG MT Notes[2020.10.26]**所涉及到的题目基本一致，只不过是将密文中的每一位的md5值与生成的随机值进行异或。我们还是只需要求出Next函数的逆即可（那篇博客也提供了对应方法，简单调参即可使用）。

不过问题是我们无法知道完全的$233$个状态，只能得知我们仅有的$104$个状态。其中一个办法就是枚举seed，枚举规模约为$43$亿，实际上跑了$16$亿多一些。（不过好像可以不用枚举seed，具体方法待更新）

Update 2021.7.20

如果我们重新观察一下代码，我们可以发现如下内容：

由于寄存器规模是$233$，而实际上只产生了$104$个随机数，因此内部的state所有内容是不变的。并且根据题目产生随机数的方式可知：在产生新的state的时候，与旧的state有如下关系：

1
2
3
4
5
6
7
8
9
10
11
def srand(self):
    for i in range(232):
        self.state[i+1] = 1812433253 * (self.state[i] ^ (self.state[i] >> 27)) - i
        self.state[i+1] &= 0xffffffff
def generate(self):
    for i in range(233):
        y = (self.state[i] & 0x80000000) | (self.state[(i+1)%233] & 0x7fffffff)
        temp = y >> 1
        temp ^= self.state[(i + 130) % 233]
        if y & 1:
            temp ^= 0x9908f23f

因此新的state[i]与旧的state[i],state[i+1],state[i+130]有关系。而题目中已经告诉了我们flag的第一位和最后一位。因此state[0],state[103]都可以求出来。有Newstate[103]=Oldstate[103]^Newstate[0]，这样我们就可以获得Oldstate[103]的最高$31$位了。

这部分结果我就略去了，算出来的Oldstate[103]可能的$32$位结果： $\text{D7FC4AA6H or D7FC4AA7H}$

然后我们分别用以下代码验证一下就行了：注：由于newstate[103]>>31==0，因此不需要考虑

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from Crypto.Util.number import *
def inverse_right(res, shift, mask=0xffffffff, bits=32):
    tmp = res
    for i in range(bits // shift):
        tmp = res ^ tmp >> shift & mask
    return tmp
def getseedbyns104(os104):
    a=os104
    for i in range(103,-1,-1):
        a=((a+i)*2520285293)&0xffffffff
        a=inverse_right(a,27)
    return a
ns103,ns0=1167644902,778501557
os104=(ns103^ns0)*2
y=os104
#os104+=2**31
a=(os104+103)*inverse(1812433253,2**32)&0xffffffff
a=inverse_right(a,27)
print(a,a&0x80000000==y&0x80000000)
print(getseedbyns104(os104))

'''
第15行注释掉:
617247885 False
2899787883
第15行不注释:
2764731549 True
1668245885
因此最终种子是1668245885，与之前爆破的情形一致。
'''

4.[ACTF新生赛2020]crypto-aes

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from Cryptodome.Cipher import AES
import os
import gmpy2
from flag import FLAG
from Cryptodome.Util.number import *

def main():
    key=os.urandom(2)*16
    iv=os.urandom(16)
    print(bytes_to_long(key)^bytes_to_long(iv))
    aes=AES.new(key,AES.MODE_CBC,iv)
    enc_flag = aes.encrypt(FLAG)
    print(enc_flag)
if __name__=="__main__":
    main()

一道AES题目，我们可以看出key是$8$组$4$位$16$进制数，我们只需要把他给出来的第一个异或结果拿出来并输出$16$进制，发现前面是$4$组$\text{C981}_h$，而后面是不规则内容。我们只需要把不规则内容用$4$组$\text{C981}_h$进行异或即可。这样我们的key和iv就都拿到了

最后我们只需要模仿他的模式，即可解出flag了

1
2
3
4
5
6
7
8
from Crypto.Util.number import *
from Crypto.Cipher import AES
iv=b'\x87lQbI0\xfc\xe6\xaa\x05P\xb1\x01\xd1pL'
cip=b'\x8c-\xcd\xde\xa7\xe9\x7f.b\x8aKs\xf1\xba\xc75\xc4d\x13\x07\xac\xa4&\xd6\x91\xfe\xf3\x14\x10|\xf8p'
key=long_to_bytes(0xc981c981c981c981c981c981c981c981c981c981c981c981c981c981c981c981)
aes=AES.new(key,AES.MODE_CBC,iv)
dec_flag = aes.decrypt(cip)
print(dec_flag)

5.[*ctf]GuessFlag(1)(2)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
from random import randint
import os
from flag import flag
N=64
key=randint(0,2**N)
# print key
key=bin(key)[2:].rjust(N,'0')
count=0
while True:
	p=0
	q=0
	new_key=''
	zeros=[0]
	for j in range(len(key)):
		if key[j]=='0':
			zeros.append(j)
	p=zeros[randint(0,len(zeros))-1]
	q=zeros[randint(0,len(zeros))-1]
	try:
		mask=int(raw_input("mask:"))
	except:
		exit(0)
	mask=bin(mask)[2:]
	if p>q:
		tmp=q
		q=p
		p=tmp
	cnt=0
	for j in range(0,N):
		if j in range(p,q+1):
			new_key+=str(int(mask[cnt])^int(key[j]))
		else:
			new_key+=key[j]
		cnt+=1
		cnt%=len(mask)
	key=new_key
	try:
		guess=int(raw_input("guess:"))
	except:
		exit(0)
	if guess==int(key,2):
		count+=1
		print 'Nice.'
	else:
		count=0
		print 'Oops.'
	if count>2:
		print flag

题目的意思很简单，服务器会保留一个随机的$64$位整数，并记录下所有的$0$位。你每次向服务器发送一个数字，然后服务器会任意选取已有密钥中$2$个$0$比特位，并将这$2$个$0$比特位之间的所有比特位依次循环异或你所发送数字的各个比特位。连续$3$次猜中密钥即可获得答案

一开始print(flag)是给出的，这次只需要发送三次$0$，这样密钥就保持不变，然后每次猜就猜他给出来的那个数，然后就可以获取flag

不过后面升级了,print(flag)这句话被删除了，这个时候就要想办法了我这个fw还问了学长，所以我自己果然是个fw。这个时候，我们只需要每次发送$1$，这样任意两个$0$之间的所有比特位都有可能被异或。不过我们多次本地实验后会发现：随着发送$1$的次数不断增多，密钥末尾的固定$1$比特位的长度越来越长，所以只需要不到$200$次的发送$1$，最后$64$个比特位就会全是$1$。所以我们每次猜密钥都猜$18446744073709551615$，也就是$2^{64}-1$，到最后就会连续$3$次猜中，最终我们就肯伊拿到flag

（这两道脑洞题个人认为质量还是挺高的，谁叫自己是个fw呢）

CTFSeason2
#ExpLog
21Jan1
http://example.com/2021/01/18/21Jan1/
作者
huangx607087
发布于
2021年1月18日
许可协议