Lfsr Notes

huangx607087学习lfsr的一些笔记

0.简介

本篇blog用在BUU上面刷的两道题来讲解lfsr，不过这仍然是一个密码学fw的笔记，很菜，别看

1. 基本概念

LFSR，中文名称叫做线性反馈移位寄存器，由多个时钟存储元件和一个反馈路径组成。其中触发器的数量又称为度。

作用就是当给定前一个状态的输出的时候，这个输出状态会继续存入移位寄存器（同时最早的数据会被删除）。

lfsr的基本Python实现代码如下（以下就是一个$24$位的lfsr）：

def lfsr(R,mask):
    output = (R << 1) & 0xffffff
    i=(R&mask)&0xffffff
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
    output^=lastbit
    return (output,lastbit)

2.解决LFSR问题的方法

PART 1[24digs]

当lfsr的位数不超过$30$位时且知道mask的情况下，可以直接采用暴力枚举法爆破seed（又称key）比如2018强网杯streamgame1

from flag import flag
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==25
def lfsr(R,mask):
    output = (R << 1) & 0xffffff
    i=(R&mask)&0xffffff
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
    output^=lastbit
    return (output,lastbit)
R=int(flag[5:-1],2)
mask=0x5311c
f=open("key","ab")
for i in range(12):
    tmp=0
    for j in range(8):
        (R,out)=lfsr(R,mask)
        tmp=(tmp << 1)^out
    f.write(chr(tmp))
f.close()

PART 2[32 digs]

在知道mask但不知道种子的情况下，我们可以用我们上面提到的式子进行移项，就可以求出之前被丢弃的一个比特位，进而不断迭代就可以得到后面的比特位，典型例题为2018 CISCN 初赛 oldstreamgame

看一下题目：

flag = "flag{xxxxxxxxxxxxxxxx}"
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==14
def lfsr(R,mask):
    output = (R << 1) & 0xffffffff
    i=(R&mask)&0xffffffff
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
    output^=lastbit
    return (output,lastbit)
R=int(flag[5:-1],16)
mask = 0b10100100000010000000100010010100
f=open("key","w")
for i in range(100):
    tmp=0
    for j in range(8):
        (R,out)=lfsr(R,mask)
        tmp=(tmp << 1)^out
    f.write(chr(tmp))
f.close()

很显然，我们知道了mask的值，而flag则为lfsr的种子，长度为$32$位。虽然爆破也是可行的，但此处不使用爆破做法，二是递推求出lfsr的种子。

$32$位的lfsr，告诉了我们只需要知道输出的最开始的$32$个数字，我们就可以递推求出seed，代码如下：

from Crypto.Util.number import *
mask = 0b10100100000010000000100010010100
b = ''
N = 32
with open('key.txt', 'rb') as f:
    b = f.read()
key = ''
print(bin(bytes_to_long(b)))
for i in range(N // 8):
    t = b[i]
    for j in range(7, -1, -1):
        key += str(t >> j & 1)
print(key)
idx = 0
ans = ""
key = key[31] + key[:32]
while idx < 32:
    tmp = 0
    for i in range(32):
        if mask >> i & 1:
            tmp ^= int(key[31 - i])
    ans = str(tmp) + ans
    idx += 1
    key = key[31] + str(tmp) + key[1:31]
num = int(ans, 2)
print (hex(num))

Update 2021.7.29 增加一个更简单易懂的脚本

from Crypto.Util.number import *
def padbin(x,l=32):
    s=bin(x)[2:]
    if(len(s)<l):
        s=(l-len(s))*'0'+s
    return s
mask=padbin(0x80000057)
state=padbin(0x155a796b)
for i in range(32):
    s=int(state[0])
    #print(len(state),len(mask))
    for j in range(31):
        s^=int(mask[j])&int(state[j+1])
    state=state+str(s&1) 
    state=state[1:]
print(hex(int(state,2))[2:])

PART 3[64 digs]

可以求出mask的，例题为**[AFCTF2018]Tiny LFSR**，64位是无法爆破的

详细内容请见文章21Jan2，发布时间为2021.1.21

PART 4[256 digs]

我们来看这样一道题目**[De1CTF2019]Babylfsr**

import hashlib
from secret import KEY,FLAG,MASK
assert(FLAG=="de1ctf{"+hashlib.sha256(hex(KEY)[2:].rstrip('L')).hexdigest()+"}")
assert(FLAG[7:11]=='1224')
LENGTH = 256
assert(KEY.bit_length()==LENGTH)
assert(MASK.bit_length()==LENGTH)
def pad(m):
    pad_length = 8 - len(m)
    return pad_length*'0'+m
class lfsr():
    def __init__(self, init, mask, length):
        self.init = init
        self.mask = mask
        self.lengthmask = 2**(length+1)-1

    def next(self):
        nextdata = (self.init << 1) & self.lengthmask 
        i = self.init & self.mask & self.lengthmask 
        output = 0
        while i != 0:
            output ^= (i & 1)
            i = i >> 1
        nextdata ^= output
        self.init = nextdata
        return output
if __name__=="__main__":
    l = lfsr(KEY,MASK,LENGTH)
    r = ''
    for i in range(63):
        b = 0
        for j in range(8):
            b = (b<<1)+l.next()
        r += pad(bin(b)[2:])
    with open('output','w') as f:
        f.write(r)

题目给出了一个长度为$256$位的lfsr和长度为$504$位的输出结果，并告诉你KEY以及FLAG的一些特征（sha256后的值前$4$位是$1224_h$）。

CTF WIKI提到：如果我们知道了$2n$位输出结果，就可以把mask求出来，进而求出key，这个算法就是BM算法，其时间复杂度为$O(n^2)$，空间复杂度为$O(n)$，$n$为lfsr的比特位数，这道题是$256$。

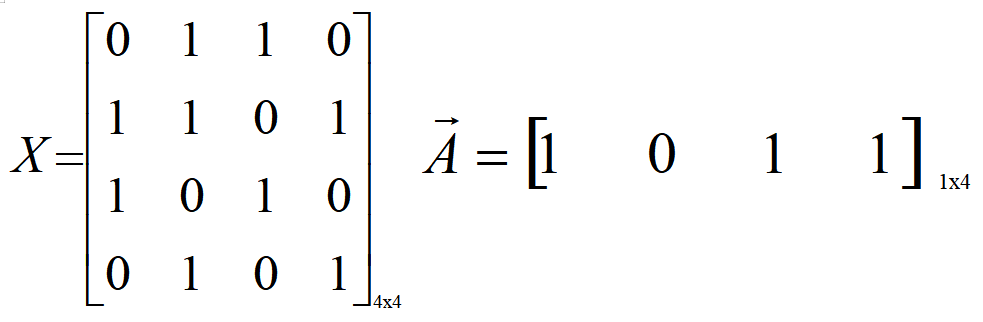
然后我们就可以得到mask的值，如下的矩阵运算

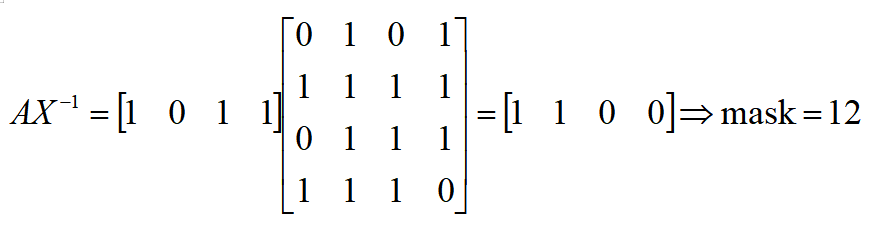
这个时候我们就求出了mask值，紧接着就是求key值了。

然后我们回到题目中：$256$位的lfsr，我们要知道$512$位才可以求出最后的结果，但目前我们只知道了$504$位，缺失$8$位，因此我们可以爆破最后$8$位，得到$256$个可能的mask值，然后我们再用这$256$个mask值恢复得到$256$个key值，根据题目给出的约束条件就可以确定最后的key值了。

上面讲的应该都算是比较详细的了，直接上一下sage的脚本，注意$\det=0$求逆矩阵会报错，因此要进行一次$\det!=0$的判断

def pad8(L,K):
    C=[]
    while K>0:
        C=[K&1]+C
        K>>=1
    if(len(C)<8):
        C=[0]*(8-len(C))+C
    return L+C
def f(x):
    num=0
    for i in range(256):
        num=num*2+x[i]
    return num
def solve(mask,key):
    idx,ans=0,''
    key=[key[255]]+key[:256]
    while idx<256:
        tmp=0
        for i in range(256):
            if mask>>i&1:
                tmp=(tmp+key[255-i])%2
        ans=str(tmp)+ans
        idx+=1
        key=[key[255]]+[tmp]+key[1:255]
    return int(ans,2)
                
#---------MAIN BELOW---------#
S=[0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0]
for i in range(256):
    Scnt=pad8(S,i)
    T=[]
    for j in range(257):
        T.append(Scnt[j:j+256])
    X=matrix(GF(2),T[0:256])
    B=matrix(GF(2),T[256])
    if(det(X)!=0):
        C=B*(X^-1)
        D=matrix(ZZ,C)
        print(hex(solve(f(D[0]),S[:256])))

只给出了所有可能的key值，最后筛选很简单的，脚本就不放了