LatticeNotes5

huangx607087学习格密码的笔记5

0. About

这个笔记接着之前发布的笔记4，继续往后面扩展新的内容。

12.格约简算法

12x01 2维高斯格约简

假如我们已知$v_1,v_2$是格$L$中的一组基底，假设$v_1$的长度小于$v_2$，（如果不小于，则交换两向量的长度）。那么我们可以用以下的脚本逐步约简二维格中最短向量的长度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
from Crypto.Util.number import *
from math import sqrt
def sgn(x):
    if x==0:
        return 0
    if x>0:
        return 1
    if x<0:
        return -1
def vecmul(veca,vecb):
    assert len(veca)==len(vecb) 
    s=0
    for i in range(len(veca)):
        s+=veca[i]*vecb[i]
    return s
def getans (veca,vecb):
    print(veca,vecb)
    if vecmul(vecb,vecb)<vecmul(veca,veca):
        tmp=veca
        veca=vecb
        vecb=tmp
    print(veca,vecb)
    m=int(vecmul(veca,vecb)/vecmul(veca,veca)+0.5*sgn(vecmul(veca,vecb)))
    if(m==0):
        return veca,vecb
    for i in range(len(vecb)):
        vecb[i]-=m*veca[i]
    return getans(veca,vecb)
a=[66586820,65354729]
b=[6513996,6393464]
A,B=getans(a,b)
print(A,B)
#[2280, -1001] [-1324, -2376]

12x02 LLL格约简算法

高斯的晶格约简算法给出了在维数$2$的晶格中找到最短非零向量的有效方法，但随着维数的增加，最短向量问题变得更加困难。 随着LLL算法的发表，1982年取得了重大进展。 在本节中，我们给出了LLL算法的完整描述，在下一节中，我们简要描述了它的一些推广。

当我们得到格$L$的一个基底时，我们肯定希望对于任意两个不同的基向量$\vec v_i,\vec v_j(i \not =j)$，使得$\cos <\vec v_i,\vec v_j>=\dfrac{\vec v_i·\vec v_j}{|\vec v_i||\vec v_j|}$越接近$0$越好。或者在更好的基上的向量尽可能短，首先是我们可以找到的最短向量，然后是长度尽可能慢地增加的向量，直到我们到达基中的最后一个向量。

前面的笔记，我提到过这样一个式子$\det L =\text{Vol }(F)≤ \prod _{i=1}^n |\vec v_i|$

其中$F$是格$L$的基本域。而如果基越正交，那么不等号两边就越接近。而为了能够得到一个更好的基底，我们可以使用施密特正交化的方法取得正交基。不过这里出现了一个问题：因为施密特正交化的方法中：由
$$
\vec v_i^*=v_i-\sum_{j=1}^{i-1}u_{ij}\vec v_j*
$$
注意到里面有这样一项$u_{ij}$并且这一项不能保证是整数。所以进行施密特正交化后的基$B^*$与原来的基$B$之间的转换出现了非整数的系数。而实际上，基$B$与基$B^*$的行列式是相同的。不过如果出现了这样两个条件，就说明$B$被约简了一次：

UPD 2021.2.9：原来这里的公式改成了图片，因为在网页上公式显示异常。

upd1

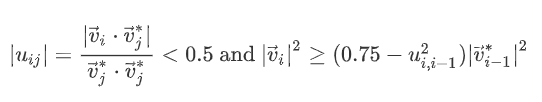
关于LLL算法一些其他的原理，以后会不定期补充。Sagemath中自带了矩阵的LLL计算，很方便。

1

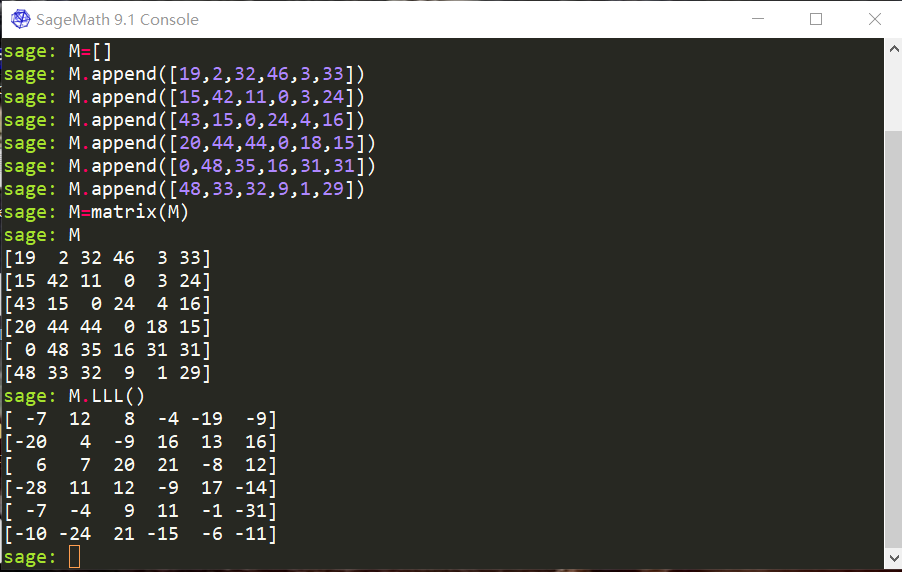
以下是用Sagemath中的LLL算法计算矩阵$M$的对应矩阵$M^{LLL}$的。可以看出，最短的向量在第一行，的确断了不少。

当然，同一个矩阵使用LLL算法后，可能会算得不同的结果。如下图的矩阵，也是$M$经过LLL算法的一个答案。不过计算一下，可以看出$M$与$M^{LLL}$的行列式绝对值相同，例子中均为$777406251$。并且$H(M)=0.47,H(M^{LLL})=0.87897$，因此$M^{LLL}$中的向量基的确更加正交。但$M_2^{LLL}$中的$H$值约为$0.88824$。查看源码可知，Sagemath中的条件$2$的判断参数是$0.99$，而$M_2^{LLL}$使用的参数是$0.75$。因此，LLL算法对其使用的参数具有比较高的依赖性。。也有用$0.85$做的，不过无论如何，最上面一行的值总是一样的（至多差一个$-1$倍）

2

12x03 使用LLL解决apprCVP问题：

我们在笔记3中解释了，如果晶格L具有正交基，那么SVP和CVP都很容易求解。 LLL算法不返回正交基，但它确实产生了一个基向量是准正交的基，即它们之间是合理正交的。 因此，我们可以将LLL算法与Babai算法相结合，形成一种求解APRCVP的算法。

这个算法很简单，先求出$M^{LLL}$中的向量作为基底，然后在Babai算法中使用LLL约简基进行计算。

13.LLL在密码分析中的应用

13x01 回顾笔记1中的同余密码系统

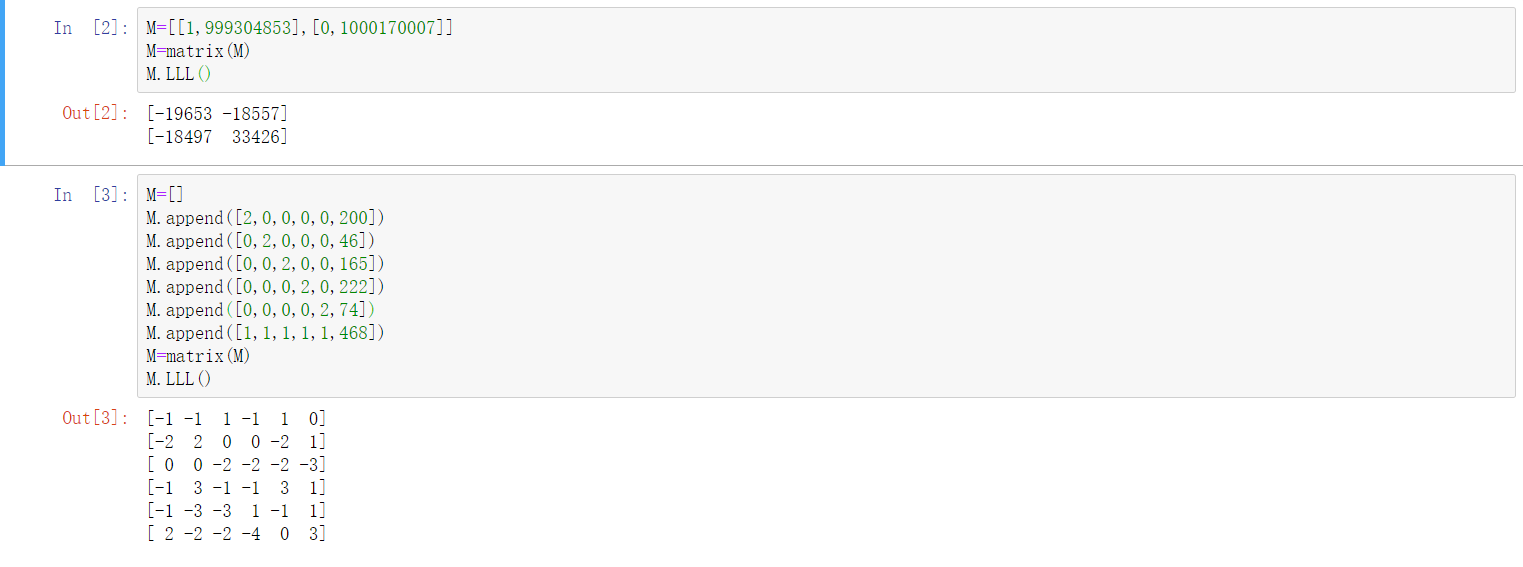
当我们知道$q=1000170007,h=999304853$时，就可以使用高斯约简向量$(1,h)$和$(0,q)$，计算约简后的向量为$(-19653, -18557)$和$(-18497, 33426)$。最短的向量为前者。因此$f=19653,g=18557$，成功破解。

13x02 回顾笔记1中背包密码中的LLL算法破解

涉及到的理论可以参见笔记1中的相关内容

下图展示了LLL在前两个例子中的体现

3

13x03 回顾笔记3中的GGH公钥密码系统

4

攻击此密码系统，可以将向量组$W$约简。得到$\vec w_1=(61,11,67),\vec w_2=(36,-30,-86),\vec w_3=(-10,102,-40)$，密文$\vec v=(−79081427, −35617462, 11035473)$

此时$H(W)$高达$0.956$。因此我们很快就找到了答案为
$$
\vec v=35\vec w_1-86\vec w_2+32\vec w_3=(79081423, 35617459, −11035471)
$$
所以最后的答案是$35,-86,32$。考虑到原来$|v_2|<|\vec v_1|<|\vec v_3|$，因此调换顺序，成功破解明文为$(-86,35,32)$

13x04 回顾笔记4中的NTRU算法

在笔记4中我们举的那个例子里，在$N=7,q=41,d=2$的情况下，我们算得$h(x)$的表达式为
$$
h(x)=20x^6+40x^5+2x^4+38x^3+8x^2+26x+30
$$
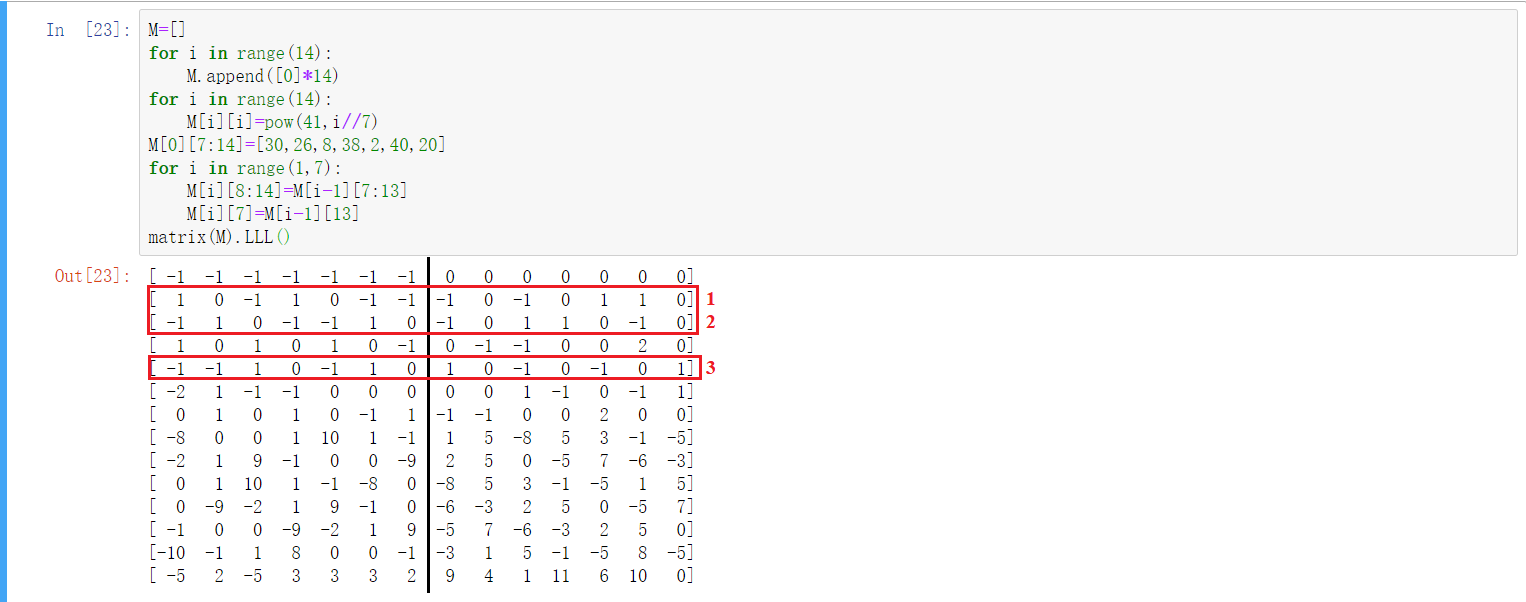
然后，我们可以构造下图的矩阵

5

同样地，我们可以使用LLL算法。算出结果后，将其对半分开，考虑到LLL算法有的时候会相差一个负号或者出现旋转的问题，因此，我们有$3$行答案符合条件，并且这$3$行互为旋转。

以用红色标出来的第一行为例：此时的$f(x)=-x^6-x^5+x^3-x^2+1,g(x)=x^5+x^4-x^2-1$。

不过，我们可以给$f(x)$乘上$-x^4$，那么有$-x^4f(x)=x^6-x^4+x^3+x^2-1$，$-x^4g(x)=x^6+x^4-x^2-x$。刚好与之前Alice和Bob所计算的结果是一样的，因此攻击者计算出来的$f(x),g(x)$也可以作为解密密钥使用。

6

14.例题选讲[UPDATE 2021.2.20]

14x01 NPUCTF2020[BABYLCG]

update 2021.2.8

STEP 1 读取题目

我们先来看一下题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
from Crypto.Util.number import *
from Crypto.Cipher import AES
from secret import flag
class LCG:
    def __init__(self, bit_length):
        m = getPrime(bit_length)
        a = getRandomRange(2, m)
        b = getRandomRange(2, m)
        seed = getRandomRange(2, m)
        self._key = {'a':a, 'b':b, 'm':m}
        self._state = seed 
    def next(self):
        self._state = (self._key['a'] * self._state + self._key['b']) % self._key['m']
        return self._state
    def export_key(self):
        return self._key
def gen_lcg():
    rand_iter = LCG(128)
    key = rand_iter.export_key()
    f = open("key", "w")
    f.write(str(key))
    return rand_iter
def leak_data(rand_iter):
    f = open("old", "w")
    for i in range(20):
        f.write(str(rand_iter.next() >> 64) + "\n")
    return rand_iter
def encrypt(rand_iter):
    f = open("ct", "wb")
    key = rand_iter.next() >> 64
    key = (key << 64) + (rand_iter.next() >> 64)
    key = long_to_bytes(key).ljust(16, b'\x00')
    iv = long_to_bytes(rand_iter.next()).ljust(16, b'\x00')
    cipher = AES.new(key, AES.MODE_CBC, iv)
    pt = flag + (16 - len(flag) % 16) * chr(16 - len(flag) % 16)
    ct = cipher.encrypt(pt.encode())
    f.write(ct)
def main():
    rand_iter = gen_lcg()
    rand_iter = leak_data(rand_iter)
    encrypt(rand_iter)

if __name__ == "__main__":
    main()

线性同余生成器简称LCG，就是通过$y\equiv ax+b\pmod m$的线性方程迭代产生随机数，随机数比较有规律可循。

题目给出$a,b,m$的同时，还给出了连续$20$个产生的数字，不过我们知道的只有它们的最高$64$位，低的$64$位不知道。

STEP 2 初步分析，确定构建格矩阵的法则

为了简便，我们可以先从两个数字开始，假设我们已知的是高位部分是$c_1,c_2$，未知的低位部分是$d_1,d_2$，那么我们可以得到
$$
c_2+d_2\equiv a(c_1+d_1)+b \pmod m
$$
去掉同余号，可以得到下面的式子，其中$k$也是未知量
$$
c_2+d_2=ac_1+ad_1+b+km
$$
如果我们对这个式子进行移项，那就有
$$
d_2=ad_1+km+ac_1+b-c_2=f(k,d_1)
$$
很显然，我们建立了$d_2$与$d_1$之间的递推关系。因此，我们要建立向量$\vec v,\vec w$和矩阵$M$，使得$\vec vM=\vec w$。而想要建立矩阵和向量，就要保证等式右边有几个未知数，向量就至少要有几维，并且两个向量要覆盖到所有的未知量。而矩阵中的数字，只能是已知量，并且还要覆盖到题目给出的所有参数。因为到时候直接放入Sagemath中进行LLL算法的是所有元素均为已知量的矩阵$M$而不是带有未知数向量。

STEP 3 从理论走向实践

根据刚刚总结的理论，我们有确定了等号右边有$2$个未知数，因此向量维数至少是$2$。然而，构造$2$维的向量很困难，因为我们上面$d_2$关于$d_1,k$的表达式实际上应该写成这个样子：
$$
d_2=ad_1+km+(ac_1+b-c_2)=f(k,d_1)+C
$$
不要小看这个$+C$的作用，因为这样我们直接就重构了表达式为$d_2=f(k,d_1)+C$。而$C$是已知量，与$k,d_1$全部无关。故我们必须要构建三维的向量，并彻底确定$\vec v=(k,d_1,1)$。矩阵$M$的第一列为$(m,a,C)^T$，向量$\vec w$的第一个分量为$d_2$。

因此，下图就表示我们构建格的雏形了。

7

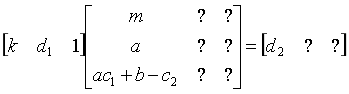
此时，未知量$k,d_1,d_2$已经全部被包含，已知量$a,b,m,c_1,c_2$也全部被包含，没有什么必要的东西了。不过注意到一个问题：$\vec w$实际上是最后对矩阵M约简时的最短向量（这个很重要）。而相对于$k$来讲，我们更希望知道的时$d_1$，因此我们就让$\vec w$的第二个分量为$d_1$，完善了矩阵。

8

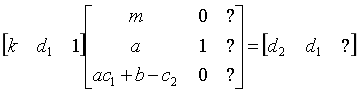
为了让最后一个数字尽可能地简单，我们可以把这个矩阵的第三列的前两个数全填成$0$。这样求最短向量的时候，最后一维也就是个固定的常数了。不过问题来了：矩阵右下角的那个数字真的可以随便取吗？

当然不是

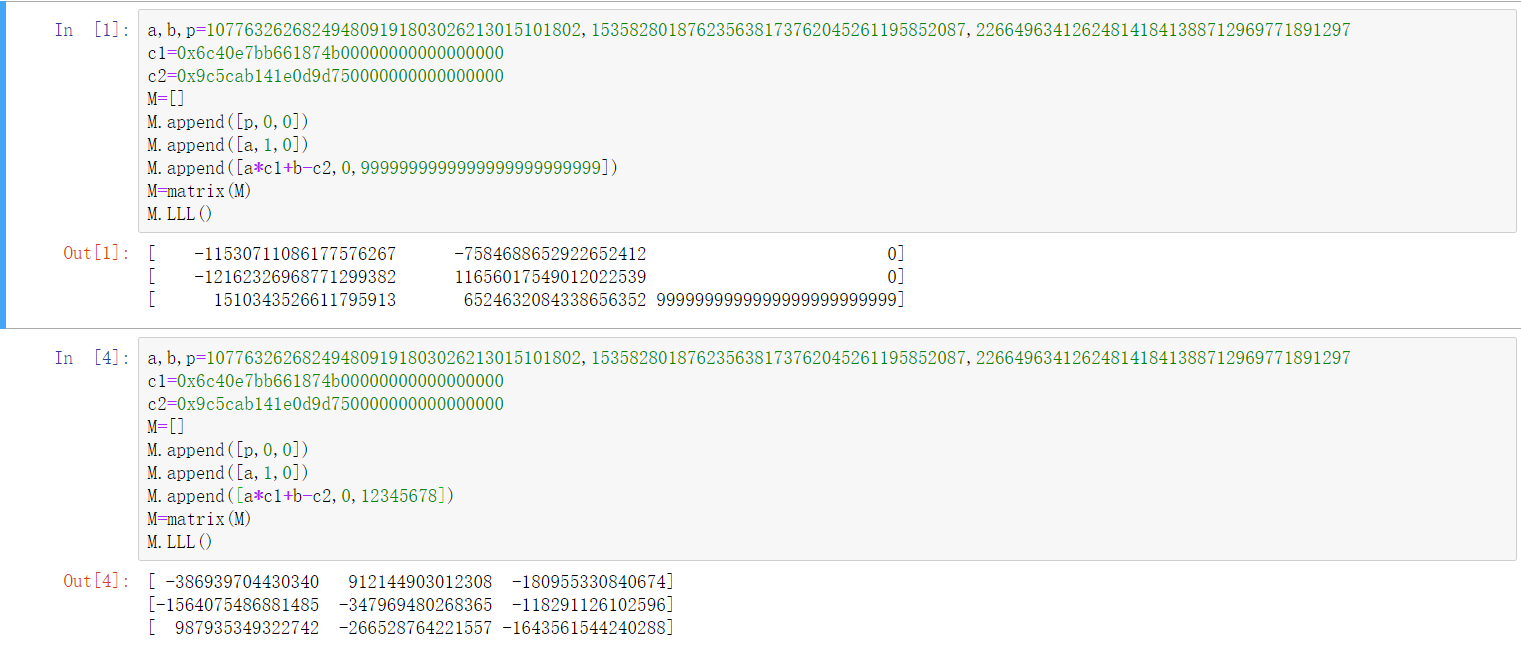
我们在笔记2的时候就讲过Hermite定理：维数为$n$的每一个格$L$中都包含一个长度不超过$\sqrt n \sqrt[n]{\det L}$的向量$\vec v$。这里$n=3$，假如右下角这个数是$x$。那么很容易计算$\det L=mx$，其中$m$是模数，$128$位。也就是说，最短向量一定小于$\sqrt[6]{27m^2x^2}$。因此提高$x$的值准确度更高。以下就是当$x$很大和较小时解出来的值。如果算出来的$d_1,d_2$中有一个时负数，那就只能换一组数据了 （直接去绝对值即可，Upd by shallow）

因此，我们就恢复了一个数的低位。一旦这个数的低位被恢复，那我们就恢复了被省略掉的低位，获得了一个状态，那我们就立刻地推出了所有的答案了，flag也就解出来了。

9

4. Reference

因为自己的做法确实有些局限性，为了获得更普遍的方法，我还是跟shallow大佬讨论了以下这道题的做法，但我可能还是太菜了，思考了两小时都没能实现这个做法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
shallow 2021/2/6 20:14:05
这题给了你这么多数据，肯定不可能只用三个就做的
shallow 2021/2/6 20:14:21
我当时这题用的hnp的思路写的来着。。
huangx607087 2021/2/6 20:14:46
我用三个做出来了
shallow 2021/2/6 20:14:55
az
huangx607087 2021/2/6 20:15:04
不过调了几次参数
shallow 2021/2/6 20:15:49
那没事了
shallow 2021/2/6 20:23:36
负的直接绝对值就行
shallow 2021/2/6 20:23:46
刚刚算了一下界居然真的够。。
huangx607087 2021/2/6 20:24:15
那，大佬能说一下你当时是怎么做的吗
shallow 2021/2/6 20:25:34
把每个d表示成ad0 + b
shallow 2021/2/6 20:25:52
然后一排全a，第二排全b，剩下地方对角线填n
shallow 2021/2/6 20:26:03
LLL完剩下的就全是di了
huangx607087 2021/2/6 20:26:14
好的，谢谢了，我过会试一下
huangx607087 2021/2/6 22:03:59
n就是他给出来的20个高位吗
huangx607087 2021/2/6 22:07:03
（不好意思我理解失误）
shallow 2021/2/6 22:07:30
n的是那个p
shallow 2021/2/6 22:07:35
就是模
shallow 2021/2/6 22:09:00
随便吧
shallow 2021/2/6 22:09:01
都可以
huangx607087 2021/2/6 22:09:05
OK
shallow 2021/2/6 22:09:15
20×22也可以，22×22也可以
huangx607087 2021/2/6 22:13:11
OK

14x02 ACTF2021 [hashgame]

Updated 2021.2.20

1.读取题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import os
from Crypto.Util.number import *
from binascii import hexlify, unhexlify
banner = '''
               _  ___        _   _           _      ____                      
 _ __ ___   __| |/ _ \      | | | | __ _ ___| |__  / ___| __ _ _ __ ___   ___ 
| '_ ` _ \ / _` | (_) |_____| |_| |/ _` / __| '_ \| |  _ / _` | '_ ` _ \ / _ \\
| | | | | | (_| |\__, |_____|  _  | (_| \__ \ | | | |_| | (_| | | | | | |  __/
|_| |_| |_|\__,_|  /_/      |_| |_|\__,_|___/_| |_|\____|\__,_|_| |_| |_|\___|
'''
def md9(m):
    n, N = 32, 2**256
    h = 69444099843545663157429813687097031070079259699713394209624552060334679683924
    g = 91404868204801963538299172115753433950696139669081509476098772951762196709558
    assert(isinstance(m, bytes) and len(m) == n)
    for x in m:
        h = ((h + x) * g) % N
    return long_to_bytes(h)
def challenge():
    for i in range(5):
        m1 = input("> ")
        m2 = input("> ")
        try:
            m1, m2 = unhexlify(m1), unhexlify(m2)
            if m1 != m2:
                if md9(m1) != md9(m2):
                    print("Failed!")
                    return
                else:
                    print("{} win!".format(i+1))
            else:
                print("Foolish try!")
                return
        except:
            print("Something your input is wrong!")
            return
    flag = os.environ.get('FLAG')
    print("Win!Here is the flag: {}".format(flag))
def main():
    print(banner)
    challenge()
if __name__ == '__main__':
    main()

Step 2：初步分析，构造矩阵

对于题目中给出的计算，我们可以进行简单地化简,在阅读题目要求后，我们可以理解为：题目要求我们找两组数字$x,y$，每组数字$32$个，并且数组$x$和数组$y$不能完全相同。最后就是找到满足条件的$2$组数字，使得
$$
hg^{32}+\sum_{i=1}^{32} x_i g^{33-i}\equiv hg^{32}+\sum_{i=1}^{32} y_i g^{33-i} \pmod{2^{256}}
$$
很显然地，我们可以约去两边的$hg^{32}$，等式变成了
$$
\sum_{i=1}^{32} x_i g^{33-i}\equiv\sum_{i=1}^{32} y_i g^{33-i} \pmod{2^{256}}
$$
然后将模式写成等式，得
$$
\sum_{i=1}^{32} x_i g^{32-i}=\sum_{i=1}^{32} y_i g^{33-i} +2^{256}k
$$
然后我们可以合并一下两边：
$$
\sum_{i=1}^{32}(x_i-y_i)g^{33-i}=2^{256}k
$$
可以顺带进行移项
$$
\sum_{i=1}^{32}(x_i-y_i)g^{33-i}-2^{256}k=0
$$

观察化简后的式子，其中未知量是$x_i-y_i$和$k$，已知量是$g$。因此我们应该建立相应的递推式。

为了简化表达，我们先假设$i$的取值从$1$到$32$缩减成$1$到$3$来模拟构造矩阵。

在只有$3$组差值的情况下，并且我们最后要求出来的是$x_i-y_i$的值，因此，$E_3=\text{diag}(1,1,1)$必须是我们构造矩阵中的一个子矩阵。并且$k$也是未知的，因此我们矩阵中还要加一个元素$k$。这样我们的向量就是$4$维行向量$(x_1-y_1,x_2-y_2,x_3-y_3,k)$，最后我们期望得到的内容就是前$3$个参量，而又因为$g^3(x_1-y_1)+g^2(x_2-y_2)+g(x_3-y_3)-2^{256}k=0$。因此我们矩阵需要增加至$5$列。最后一列为列向量$(g^3,g^2,g,2^{256})^T$，负号扔给$k$。而最后我们得到的向量就是$(x_1-y_1,x_2-y_2,x_3-y_3,-k,0)$，向量的最后一列必须是$0$。

所以我们可以尝试构造一个这样的矩阵及其计算方式。

10

我们到最后只需要找到尾数是$0$的那一列，那么就成功了。

但这样好像是失败了（，因为LLL算法后结出来的最后的结果不为$0$。

看来，这里的计算应该是跟上面那个例子除了相同的问题。

Step 3：构造并调整矩阵

因此我们现在就需要对上面的矩阵进行调整。因为最短向量总是小于$\sqrt n \sqrt[n]{\det L}$。当格$L$对应的矩阵$M$不是方阵的时候，我们规定格$L$的行列式$\det L=\det MM^T$。而当$\det L$太小的时候，就会导致最后解出来的向量更短，导致计算错误。因为：
$$
a^2+b^2<(a+b)^2
$$
这就意味着符合条件时，最后一个$0$参数会被微小提升，来缓解其他分量的负担，向量长度变小了，但却不是我们想要的结果。

因此我们就要扩大$\det L$。而我们又想保持住等号右边的向量的形式，因此我们就需要对矩阵最右边一列所有数字同时乘上一个数$C$（不取模），然后这样格$L$的行列式就会提升到原来的$C^8$倍（如果构造出的是$M$规模是$33\text x34$，则$MM^T$就是$33\text x33$方阵，最右边乘上$C$就会导致矩阵行列式提升到原来的$C^{66}$倍）。而向量的长度，提升倍数将会小于$\sqrt[33]{C^{66}}=C^2$倍。

因此，我们最后期望得到的矩阵计算是这样的，而在这道题中，$C$取$70$多就够了，然而我还是取了$2^{700}$为了保险。

11

构造矩阵运行了一下，可以发现，向量的所有分量都小于$255$。然后我们就可以构造一段模板$x$和一段变化过的$y$就行了。

这里有个问题：解出来的值有正有负，这个时候我们可以把所有正数都基于$\text{00H}$作为模板，负数基于$\text{FFH}$作为模板。例如，假如解出来的前$4$个数字是$32,-64,-96,128$，那么我们$x$组就构造$\text{00FFFF00H}$，$y$组构造$\text{20BF9F80}$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#Sagemath 9.1
from Crypto.Util.number import *
from os import urandom
mod=2^256
K,n=2^700,32
g=91404868204801963538299172115753433950696139669081509476098772951762196709558
M=[[0 for _ in range(n+2)]for __ in range(n+1)]
for i in range(n+1):
    ge=ZZ(pow(g,n-i,mod))
    M[i][i]=1
    M[i][n+1]=ZZ(ge*K)
M[n][n+1]=ZZ(K*mod)
M=matrix(M)
A=M.LLL()
B,D=A[0],[]
for i in B:
    if i<0:
        D.append(255)
    else:
        D.append(0)
B=list(B)
print(B,len(B))
print(D,len(D))
s,t="",""
def padhex(x,l):
    s=hex(x)[2:]
    return '0'*(l-len(s))+s
for i in range(32):
    s+=padhex(D[i],2)
    t+=padhex(B[i]+D[i],2)
print(s)
print(t)
'''
b=[64, -39, 118, 7, 39, -3, 102, -7, -9, -9, -32, -48, 69, 58, 120, 133, 23, -197, 53, 23, -41, -45, 61, -101, 26, 2, -74, -57, 24, -23, -60, 52, -16, 0] 34
d=[0, 255, 0, 0, 0, 255, 0, 255, 255, 255, 255, 255, 0, 0, 0, 0, 0, 255, 0, 0, 255, 255, 0, 255, 0, 0, 255, 255, 0, 255, 255, 0, 255, 0] 34
s=00ff000000ff00ffffffffff0000000000ff0000ffff00ff0000ffff00ffff00
t=40d8760727fc66f8f6f6dfcf453a7885173a3517d6d23d9a1a02b5c618e8c334
'''

4.Reference

一开始自己想的是构造$64\text{x}64$的矩阵，想分出$y_{32}$，构造从$(x_1,x_2,…,x_{32},y_1,y_2,…,y_{31},k)$递推出$(x_1,x_2,…,y_{32},y_1,y_2,…,y_{31},k)$的想法，不过发现这样做构造矩阵并不可以。可能是因为这种构造下，$x_1$和$y_1$孤立，导致直接出$0$解。也就是说，这样由于是构造的方阵，可以直接使得LLL之后的向量结果，每一行的行向量都是单位矩阵中对应行向量的某个整数的倍数，直接构造出了$H(B)=1$的完全正交基……。

这件事还是暴露了一个严重的问题就是：huangx607087 is a feiwu

15.总结

到这里为止，格密码的5篇笔记全部投放完毕。由于最后一篇限于时间，没有过多地提及LLL算法的原理，仅仅是简单地提了一下LLL算法的使用方法，和解决了之前所抛出来的几个问题。后面主要就是将这些算法应用到CTF中的题目里去。可能会投放Notes6。但Notes6大概率会属于ExpLog。

以后有可能会对LLL算法的相关原理进行补充。

CTFSeason2
#Notes
LatticeNotes5
http://example.com/2021/02/06/LatticeNotes5/
作者
huangx607087
发布于
2021年2月6日
许可协议