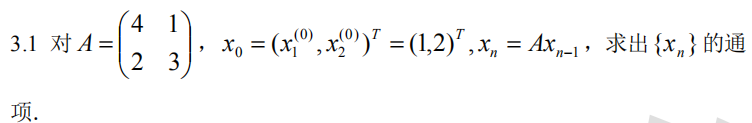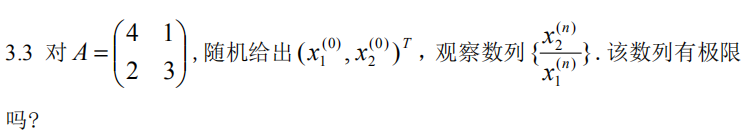MatlabExperiment1-4

Matlab Experiment By huangx607087

Notice

2月25日更新：4篇文章合一，因为自己的博客主要还是搞CTF而不是matlab（，因此这里主要还是以工具查阅的方式发布

Div 1

1

计算$\lim_{x\rightarrow0} \dfrac{1-\cos(mx)}{x^2}$和$\lim_{x\rightarrow0} \dfrac{1-\cos(mx)}{x}$，其中$m$为自己学号的后4位，本博客中用的数值是$m=1126$

1
2
3
4
5
6
7
8
>> syms x
>> f=(1-cos(1126*x))/(x*x);
>> limit(f,x,0)
%633938
>> syms x
>> g=(1-cos(1126*x))/(x);
>> limit(g,x,0)
%0

2

$f(x)=e^x\sin(\dfrac{mx}{1000})$，求$f’’(x)$和$f^{(6)}(1)$，此处$m=1126$。

1
2
3
4
5
6
7
>> syms x
>> f=exp(x)*sin(1126*x/1000);
>> d1=diff(f,x,2);
>> d2=diff(f,x,6);
>> k=subs(d2,x,1);
%(563*cos((563*x)/500)*exp(x))/250 - (66969*sin((563*x)/500)*exp(x))/250000
%(63380945166868791*exp(1)*sin(563/500))/15625000000000000 - (170878640482871*cos(563/500)*exp(1))/15625000000000

3

计算$\int_{0}^{+∞} e^{-mx^2} \text dx$，其中$m=1126$。

1
2
3
4
>> syms x
>> f=exp(-1126*x*x);
>> int(f,x,0,inf)
%(1126^(1/2)*pi^(1/2))/2252

4

给出$\sqrt[3]{\dfrac{m}{1000}+x}$在$x=0$处的泰勒展开式，其中$x$的最高次幂为$4$，$m=1126$。

1
2
3
4
5
>> syms x
>> f=(1126/1000+x)^(1/3);
>> taylor(f,x,0,'Order',5)
%  -(1250000000*500^(2/3)*563^(1/3)*x^4)/24414051311523 + (1250000*500^(2/3)*563^(1/3)*x^3)/14454737307 - (500*500^(2/3)*563^(1/3)*x^2)/2852721 + (500^(2/3)*563^(1/3)*x)/1689 + (500^(2/3)*563^(1/3))/500

5

数列$x$满足$x_1=2,x_2=1,x_n=2x_{n-1}+\dfrac m {300}x_{n-2}$，用循环语句给出这个数列的前$20$项，并用向量的形式输出。其中$m=1126$。

1
2
3
4
5
6
>> x=[2,1];
>> for n=3:20
x(n)=2*x(n-1)+(1126/300)*x(n-2);
end
sym(x)
%[ 2, 1, 713/75, 683/30, 5714999122138853/70368744177664, 545095937007935/2199023255552, 1760513646050073/2199023255552, 1391738510584149/549755813888, 4435425659045283/549755813888, 3523627465287435/137438953472, 2802290668494757/34359738368, 8910918441917557/34359738368, 7084941964896359/8589934592, 5632823933614673/2147483648, 4478421269405941/536870912, 3560577249130079/134217728, 2830851614013183/33554432, 562669471674589/2097152, 7157638204545749/8388608, 5690705185958165/2097152]

6

T6

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
>> A=[4,-2,2;-3,0,5;1,2,5];
>> B=[1,1126/400,4;-2,0,-3;2,-1,1];
det(A)
ans = -92
sym(A^-1)
ans =
[  5/46, -7/46,  5/46]
[ -5/23, -9/46, 13/46]
[  3/46,  5/46,  3/46]
>> [P,D]=eig(A)
P =
   -0.3490   -0.8942    0.2379
   -0.8952    0.4403    0.5181
    0.2772   -0.0815    0.8216
D =
   -2.7180         0         0
         0    5.1671         0
         0         0    6.5509
>> A*(B^-1)
ans =
    0.0000    0.0000    2.0000
   -3.0351   -8.5615   -8.5439
    0.1597   -1.9704   -1.5503
>> (A^-1)*B
ans =
    0.6304    0.1973    1.0000
    0.7391   -0.8946    0.0000
   -0.0217    0.1184    0.0000

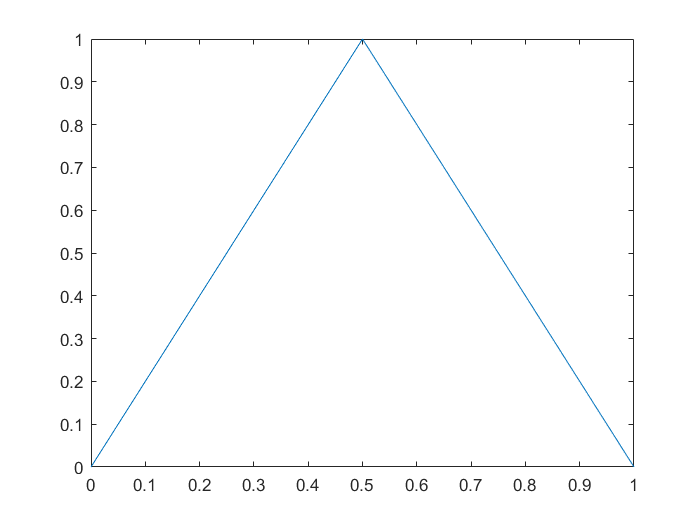
7

作图$f(x)$，其中$x\in [0,0.5]$时$f(x)=2x$，$x\in [0.5,1]$时$f(x)=2(1-x)$

使用的M文件：

1
2
3
4
5
6
7
8
9
function [y]=f(x)
if x>=0 && x<=0.5
    y=2*x;
elseif 0.5<x && x<=1
    y=2*(1-x);
else
    y=0
end
end

绘图指令：

fplot('f',[0,1])

图片：

7

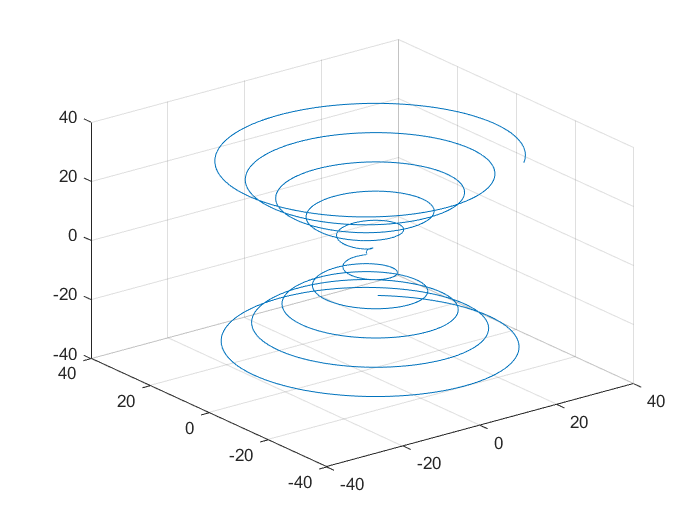
8

绘制空间曲线$x=\cos t+t \sin t,y=\sin t-t\cos t,z=-t$，其中$t \in[\dfrac{-30m}{1000},\dfrac{+30m}{1000}]$，$m=1126$。

1
2
3
4
5
>> t=-30*1126/1000:0.005:30*1126/1000;
x=cos(t)+t.*sin(t);
y=sin(t)-t.*cos(t);
z=-t;
plot3(x,y,z);grid on
8

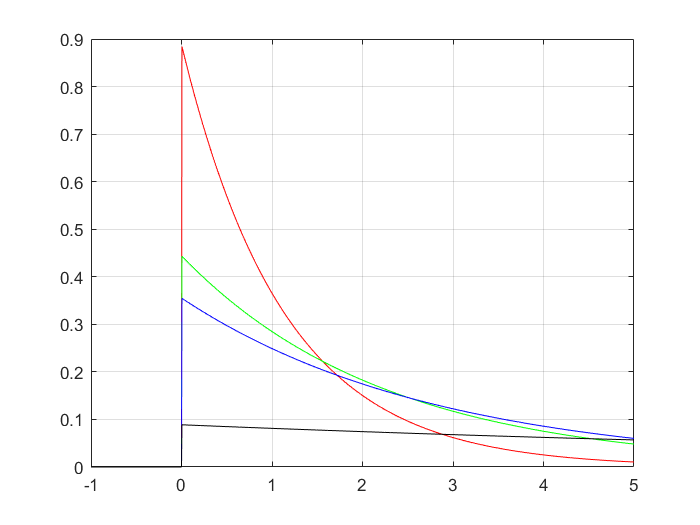
9

$f(x)=\lambda e^{-\lambda x}, x>0$，$x≤0$时$x$恒定为$0$，在同意坐标系内画出$f(x)$的图像，$\lambda$分别取$\dfrac{1000}{1126},\dfrac{500}{1126},\dfrac{400}{1126},\dfrac{100}{1126}$。

1
2
3
4
5
6
>> x=-1:0.005:5;
f1=(0) .* (x<=0) +(1000/1126*exp(-1000/1126*x)) .* (x>0);
f2=(0) .* (x<=0) +(500/1126*exp(-500/1126*x)) .* (x>0);
f3=(0) .* (x<=0) +(400/1126*exp(-400/1126*x)) .* (x>0);
f4=(0) .* (x<=0) +(100/1126*exp(-100/1126*x)) .* (x>0);
plot(x,f1,'r',x,f2,'g',x,f3,'b',x,f4,'k'); grid on
9

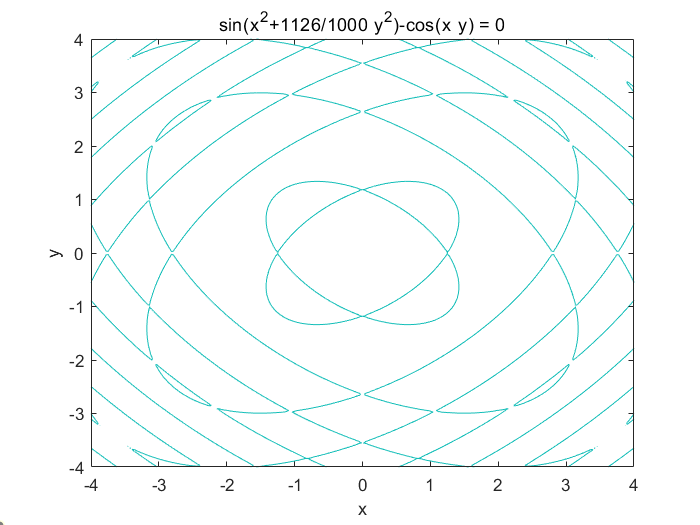
10

用ezplot画隐函数$\sin (x^2+\dfrac{m}{1000}y^2)=\cos (xy)$，$m=1126$

1
ezplot('sin(x^2+1126/1000*y^2)-cos(x*y)',[-4 4 -4 4])
10

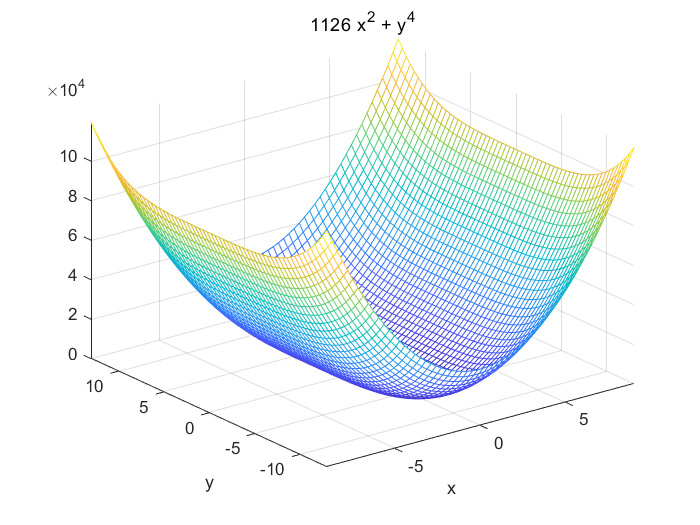
11

作图$z=mx^2+y^4$的图形，$m=1126$。

1
2
3
syms x
syms y
ezmesh(1126*x^2+y^4,[-9,9,-13,13])
11

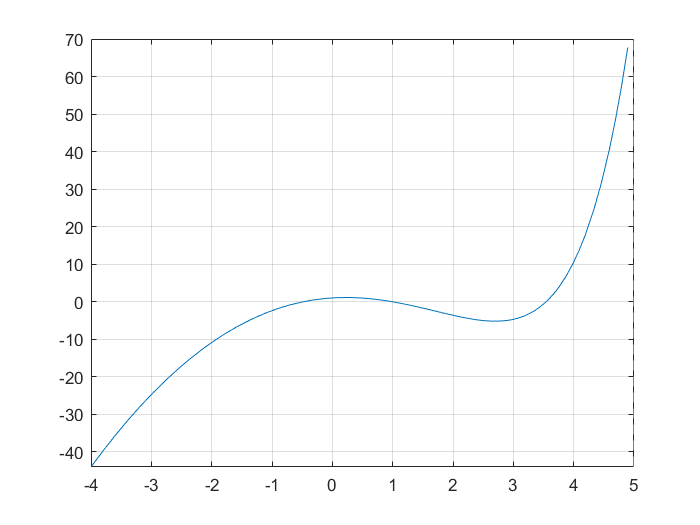
12

对于方程$e^x-3 \dfrac{m}{m+100}x^2=0,m=1126$。

1.绘制函数的图形
2.借助于软件中方程近似求根命令求出所有实根。
3.找出单调区间，并说明为什么这些区间是单调的
4.说明该方程确实只有你求出的这些实根
5.写出你做此题的体会

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
%1-3问
syms x
f=exp(x)-3*1126/1226*x^2;
fplot(f,[-4,5]);grid on
double(solve(f,x));
%图片见下图
ans =
    0.9867
   -0.4751
    3.5441
df=diff(f,x);
double(solve(df))
ans =
    0.2279
    2.6998
12

对于$f(x)=e^x-\dfrac{1689}{613}x^2$，定义域是$R$。求导得$f’(x)=e^x-\dfrac{3378}{613}x$。这个方程有两个根大致为$0.2279$和$2.6998$。因此$f(x)$在区间$[-∞，0.2279]$和$[2.6998,+∞]$这两个区间内单调增，在区间$[0.2279,2.6998]$单调减。因此$f(x)$在这三个单调区间内至多各有一个实根，我们已经求出来为$-0.4751,0.9867,3.5441$。

体会略去（

Div 2

1

$x_{1}=-1,x_{n+1}=0.5(x_n+\dfrac{1126}{x_n})$。问数列$x_n$是否收敛，若收敛其值是多少，精确到$8$位有效数字

Code

1
2
3
4
5
6
7
syms x;
f=inline('0.5*(x+1126/x)');
x1=-1;
for i=1:1:15
x1=f(x1);
fprintf('%g,%.8f\n',i,x1);
end

Result

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1,-563.50000000
2,-282.74911269
3,-143.36572086
4,-75.60988006
5,-45.25105685
6,-35.06722679
7,-33.58849003
8,-33.55593926
9,-33.55592347
10,-33.55592347
11,-33.55592347
12,-33.55592347
13,-33.55592347
14,-33.55592347
15,-33.55592347

因此$x$值是收敛的，收敛到$-33.55592347$。

2

求出分式线性函数$f_1(x)=\dfrac{x-1}{x+1126},f_2(x)=\dfrac{x+1126^2}{x+1126}$的不动点，再编程判断它们的迭代序列是否收敛。

f1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
syms x
f1=(x-1)/(x+1126);
fprintf("%.8f\n%.8f\n",solve(f1-x,x))
%-1124.99911111
%-0.00088889
f1=inline('(x-1)/(x+1126)');
x1=-1;
for i=1:1:15
x1=f1(x1);
fprintf('%g,%.8f\n',i,x1);
end
1,-7.94444444
2,-0.00800000
3,-0.00089521
4,-0.00088890
5,-0.00088889
6,-0.00088889
7,-0.00088889
8,-0.00088889
9,-0.00088889
10,-0.00088889
11,-0.00088889
12,-0.00088889
13,-0.00088889
14,-0.00088889
15,-0.00088889
%收敛于0.00088889

f2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
syms x
f2=(x+1126*1126)/(x+1126);
fprintf("%.8f\n%.8f\n",solve(f2-x,x))
%-1821.18274398
%696.18274398
f2=inline('(x+1126*1126)/(x+1126)');
x1=-1;
for i=1:1:30
x1=f2(x1);
fprintf('%g,%.8f\n',i,x1);
end
1,1127.00000000
2,563.25033289
3,750.88885622
4,675.92009226
5,704.00009720
6,693.21307799
7,697.31755363
8,695.75007109
9,696.34785265
10,696.11975892
11,696.20677431
12,696.17357627
13,696.18624158
14,696.18140961
15,696.18325306
16,696.18254976
17,696.18281808
18,696.18271571
19,696.18275477
20,696.18273987
21,696.18274555
22,696.18274338
23,696.18274421
24,696.18274390
25,696.18274402
26,696.18274397
27,696.18274399
28,696.18274398
29,696.18274398
30,696.18274398
%收敛于696.18274398

3

$f(x)=2x,x\in[0,0.5]; 2(1-x),x\in(0.5,1]$的迭代是否会产生混沌。

不会产生混沌，只不过如果小数位数增多，周期会变长。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
syms x
f=inline('(2*x) .*(x>=0&x<=0.5) + (2*(1-x)) .* (x>0.5&x<=1)')
x0=0.53;
for i=1:1:50
x0=f(x0);
fprintf('%g,%g\n',i,x0)
end
-------------------Result-----------------
1,0.94
2,0.12
3,0.24
4,0.48
5,0.96
6,0.08
7,0.16
8,0.32
9,0.64
10,0.72
11,0.56
12,0.88
13,0.24
14,0.48
15,0.96

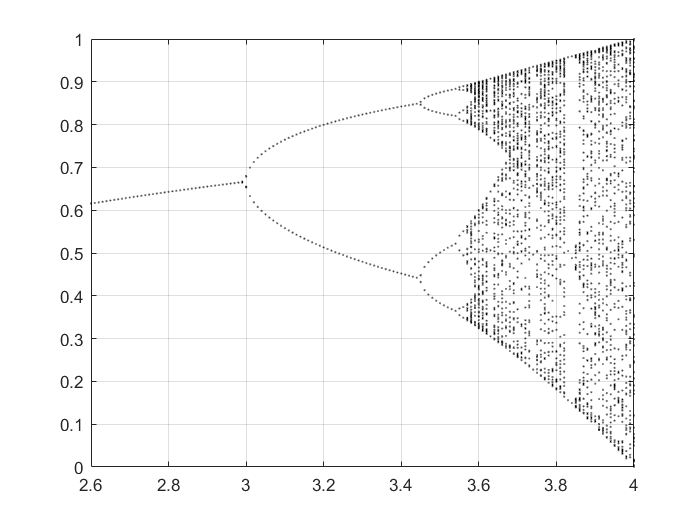
4

$f(x)=\alpha x(1-x),x\in[0,1]$，其中$x_0=0.5$产生迭代序列的收敛性。其中$\alpha$分别取$2.6,3.4,3.6,3.84$。出现循环，指出周期。

1
2
3
4
5
6
7
8
9
10
11
u=2.6:0.01:4.0;
x=0.1;
for i=1:300
x=u.*(x-x.^2);
end
for j=1:80
x=u.*(x-x.^2);
plot(u,x,'k.','markersize',2)
hold on;
end
grid on
4

$2.6$对应的周期是$1$，$3.4$对应的周期是$2$，$3.6$出现了混沌现象，$3.84$对应的周期是$3$。

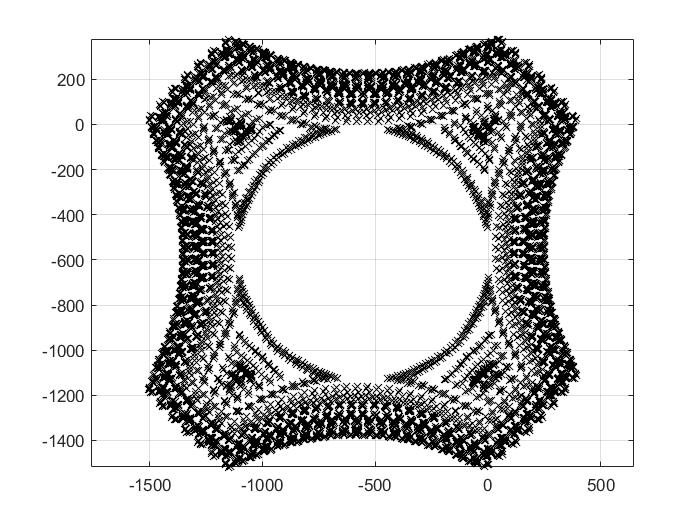
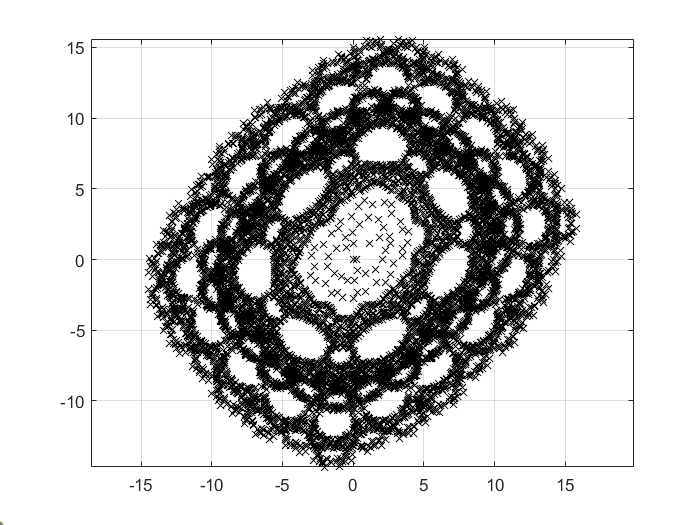
5

对于 Martin 迭代，取参数 $a,b,c$为下面的值会得到什么图形？

$a$ $b$ $c$
$\mathbf{1}$ $-1126$ $1.126$ $-1126$
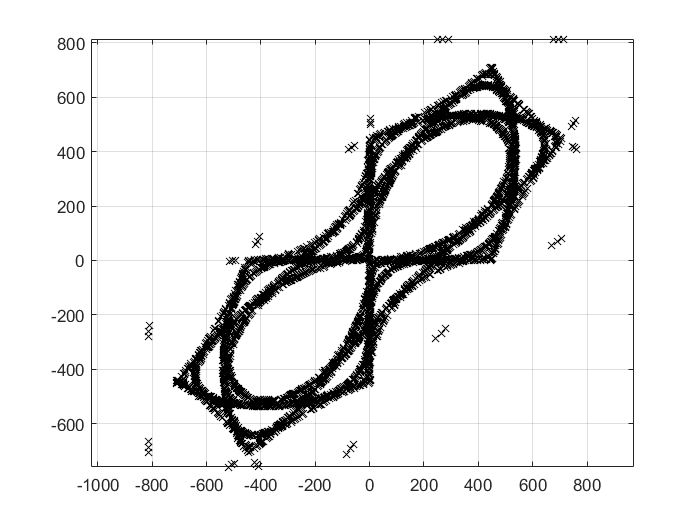
$\mathbf{2}$ $1.126$ $1.126$ $0.5$
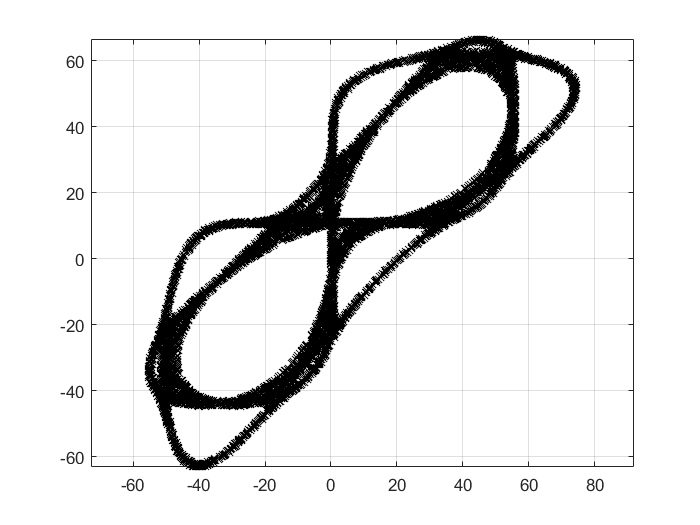
$\mathbf{3}$ $1.126$ $1126$ $-1126$
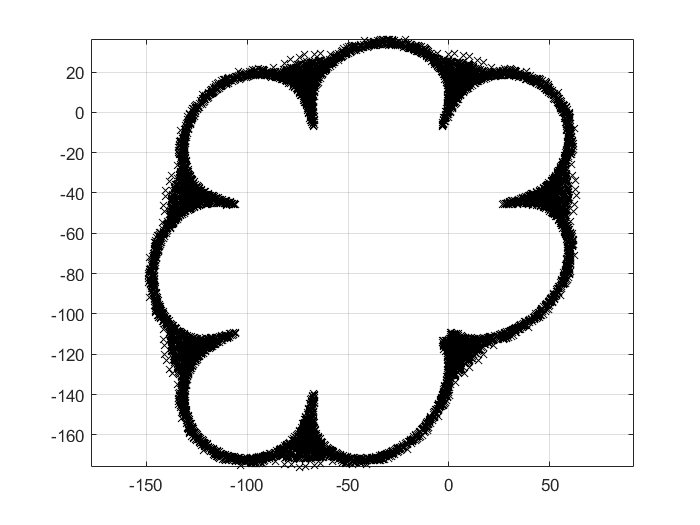
$\mathbf{4}$ $11.26$ $112.6$ $-10$
$\mathbf{5}$ $-112.6$ $17$ $4$ 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
%输入edit，填写以下代码
function Martin(a,b,c,n)
f=@(x,y)(y-sign(x)*sqrt(abs(b*x-c)));
g=@(x)(a-x);
m=[0;0];
for n=1:n
m(:,n+1)=[f(m(1,n),m(2,n)),g(m(1,n))];
end
plot(m(1,:),m(2,:),'kx');grid on
axis equal
%关闭edit
Martin(-1126,1.126,-1126,10000)
Martin(1.126,1.126,0.5,10000)
Martin(1.126,1126,-1126,10000)
Martin(11.26,112.6,-10,10000)
Martin(-112.6,17,4,10000)
5-1 5-2 5-3 5-4 5-5

6

寻找分式函数$f(x)=\dfrac{ax+b}{cx^2+dx+e}$，使它产生的迭代序列收敛到$\sqrt[3]{1126}$。如果迭代收敛，那么迭代的初值和收敛的速度成什么关系？

根据题目我们可以知道$\sqrt[3]{1126}$是方程$f(x)=x$的解。因此，我们可以得到：
$$
cx^3+dx^2+(e-a)x-b=0
$$
很显然，三次根号只能通过直接开三次根号实现，因此$c=1,b=1126$。为保证这个，只有$d=0,e=a$。

不过，这里有个小细节，为了保证点最后收敛于我们的期望值，因此我们期望值的导数的绝对值要小于$1$。这里我们通过试验，选取的值为$500$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
%求收敛值的程序
syms x;
f=inline('(500*x+1126)/(x^2+500)');
x1=-1;
for i=1:1:15
x1=f(x1);
fprintf('%g,%.8f\n',i,x1);
end
1,1.24950100
2,3.49060158
3,5.60599142
4,7.39329141
5,8.69476637
6,9.50902199
7,9.95985241
8,10.19015330
9,10.30253816
10,10.35609816
11,10.38132871
12,10.39314826
13,10.39867078
14,10.40124793
15,10.40244990
%求导数程序
syms x;
y=(500*x+1126)/(x^2+500);
dy=diff(y,x);
double(subs(dy,x,1126^(1/3)))

如果迭代初值的函数值越接近于函数的吸引点的横坐标，那么收敛的速度越快。

Div 3

1

T1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
syms n
A=[4,1;2,3];
x=[1;2];
[P,D]=eig(sym(A))
P =
[ -1/2, 1]
[    1, 1]
D =
[ 2, 0]
[ 0, 5]
An=P*D^n*(P^-1)
[     2^n/3 + (2*5^n)/3,     5^n/3 - 2^n/3]
[ (2*5^n)/3 - (2*2^n)/3, (2*2^n)/3 + 5^n/3]
xn=An*x
     (4*5^n)/3 - 2^n/3
 (2*2^n)/3 + (4*5^n)/3

2

将上面的矩阵第一行改为$0.4,0.2$，第二行改为$0.1,0.3$，再做一次实验求$x$通项。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
syms n
A=[0.4,0.2;0.1,0.3];
x=[1;2];
[P,D]=eig(sym(A))
P =
[ -1, 2]
[  1, 1]
D =
[ 1/5,   0]
[   0, 1/2]
An=P*D^n*(P^-1)
An =
[ (2*(1/2)^n)/3 + (1/5)^n/3, (2*(1/2)^n)/3 - (2*(1/5)^n)/3]
[     (1/2)^n/3 - (1/5)^n/3,     (1/2)^n/3 + (2*(1/5)^n)/3]
xn=An*x
xn=
 2*(1/2)^n - (1/5)^n
   (1/2)^n + (1/5)^n

3

T3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
A=[4,1;2,3];
a=[];
x=2*rand(2,1)-1;
for i=1:30
a(i,1:2)=x;
x=A*x;
end
for i=1:20
if a(i,1)==0
break
else t=a(i,2)/a(i,1);
fprintf('%g  %g\n',i,t);
end
end
%以下为输出结果
1  1.28936
2  1.10941
3  1.04283
4  1.01699
5  1.00677
6  1.0027
7  1.00108
8  1.00043
9  1.00017
10  1.00007
11  1.00003
12  1.00001
13  1
14  1
15  1
16  1
17  1
18  1
19  1

这个数列最终收敛于$1$。

4

$x_n,y_n,m(x_n)$极限都存在，见代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
A=[2.1,3.4,-1.2,2.3;0.8,-0.3,4.1,2.8;2.3,7.9,-1.5,1.4;3.5,7.2,1.7,-9];
x0=[1;2;3;4];
x=A*x0;
for i=1:1:100
a=max(x);
b=min(x);
m=a*(abs(a)>abs(b))+b*(abs(a)<=abs(b));
y=x/m;
x=A*y;
end
%以下为结果
x =
    0.9819
    3.2889
   -1.2890
  -11.2213
y =
   -0.0875
   -0.2931
    0.1149
    1.0000
m =
  -11.2213

5

求出上一题矩阵$A$的所有特征值和特征向量，并与上一题的结论做对比

1
2
3
4
5
6
7
8
9
10
11
12
A=[2.1,3.4,-1.2,2.3;0.8,-0.3,4.1,2.8;2.3,7.9,-1.5,1.4;3.5,7.2,1.7,-9];
[P,D]=eig(A)
P =
    0.3779    0.8848   -0.0832    0.3908
    0.5367   -0.3575   -0.2786   -0.4777
    0.6473   -0.2988    0.1092    0.7442
    0.3874    0.0015    0.9505   -0.2555
D =
    7.2300         0         0         0
         0    1.1352         0         0
         0         0  -11.2213         0
         0         0         0   -5.8439

$A$中绝对值最大的特征值等于$m(x_n)$的极限值。

并且$P$的特征值$-11.2213$对应的特征向量约为上题中向量$\vec y$的$\dfrac{20}{19}$倍。

6

已知矩阵$A=[0.75,0.5,0.25;0.125,0.25,0.5;0.125,0.25,0.25]$为天气矩阵，向量$\vec p_0=(0.5,0.25,0.25)^T$，求出若干天之后的天气情况，保留$4$位小数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
A=[3/4,1/2,1/4;1/8,1/4,1/2;1/8,1/4,1/4];
P=[0.5;0.25;0.25];
for i=1:1:25
P(:,i+1)=A*P(:,i);
end
P
%以下为输出结果
  列 1 至 10
    0.5000    0.5625    0.5938    0.6035    0.6069    0.6081    0.6085    0.6086    0.6087    0.6087
    0.2500    0.2500    0.2266    0.2207    0.2185    0.2178    0.2175    0.2174    0.2174    0.2174
    0.2500    0.1875    0.1797    0.1758    0.1746    0.1741    0.1740    0.1739    0.1739    0.1739
  列 11 至 20
    0.6087    0.6087    0.6087    0.6087    0.6087    0.6087    0.6087    0.6087    0.6087    0.6087
    0.2174    0.2174    0.2174    0.2174    0.2174    0.2174    0.2174    0.2174    0.2174    0.2174
    0.1739    0.1739    0.1739    0.1739    0.1739    0.1739    0.1739    0.1739    0.1739    0.1739
  列 21 至 26
    0.6087    0.6087    0.6087    0.6087    0.6087    0.6087
    0.2174    0.2174    0.2174    0.2174    0.2174    0.2174
    0.1739    0.1739    0.1739    0.1739    0.1739    0.1739

得出结论：第$9$天开始，天气向量稳定于$(0.6087,0.2174,0.1739)^T$. 总感觉最后结果中的第一个分量缺了点什么。

7

求出第六题的矩阵$A$的特征值和特征向量，并与最终的结论进行对比。

1
2
3
4
5
6
7
8
9
10
11
12
A=[3/4,1/2,1/4;1/8,1/4,1/2;1/8,1/4,1/4];
[P,D]=eig(A)
P =

   -0.9094   -0.8069    0.3437
   -0.3248    0.5116   -0.8133
   -0.2598    0.2953    0.4695
D =

    1.0000         0         0
         0    0.3415         0
         0         0   -0.0915

矩阵$A$有特征值$1$，对应向量是$\alpha=(-0.9094,-0.3248,-0.2598)^T$，上题中的最终结果恰好是$\alpha$的$0.6696$倍。

8

A=[3/4,7/18;1/4,11/18]，设 $p_1$,$ p_2$ 为 $A$ 的 两 个 线 性 无 关 的 特 征 向 量 ， 若$p^{(0)}=(0.5,0.5)^T$。具体求出上述的$u$, $v$ ，将 $p^(0)$ 表示成 $p_1$,$ p_2 $的线性组合， 求 $p^{(k)}$ 的具体表达式，并求 $k\rightarrow +∞$ 时$ p^{(k)}$ 的极限，与已知结论作比较.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A=[0.75,7/18;0.25,11/18];
p0=[0.5;0.5];
[P,D]=eig(sym(A));
B=sym(P^-1)*p0
B =
 5/46
 9/23
syms k
pk=B(1,1)*D(1,1) .^ k*P(:,1)+B(2,1)*D(2,2) .^ k*P(:,2)
pk =
 14/23 - (5*(13/36)^k)/46
  (5*(13/36)^k)/46 + 9/23
vpa(limit(pk,k,100),10)
ans =
 0.6086956522
 0.3913043478

结论：与上课时迭代出来的极限值是一样的。

Div 4

1

用求定积分的 Monte Carlo 法近似计算$\pi$

1
2
3
4
5
6
7
8
9
10
n=500000;
kount=0;
for i=1:n
x=rand;y=rand;
if(x^2+y^2<=1)
kount=kount+1;
end
end
ans=4*kount/n
%三次运行结果：3.1398 3.1424 3.1507

2

根据任取一对正整数互质概率的讨论结果，现选取$112600$ 对随机的 $a,b$ 求出$\pi$ 的近似值。

提示：(1)最大公约数的命令:gcd(a,b)

(2)randint(1,1,[u,v])产生一个在$[u,v]$区间上的随机整数

1
2
3
4
5
6
7
8
9
10
kount=0;
for i=1:112600
a=ceil(rand*500000000);
b=ceil(rand*500000000);
if gcd(a,b)==1;
kount=kount+1;
end
end
sqrt(6*112600/kount)
%三次运行结果：3.1377 3.1464 3.1394

3

求满足$c-b=2,c<1000$的所有勾股数，能否类似于书中的（11.8），

把它们用一个公式表示出来？公式:$a=2(u+1),b=u^2+2u,c=u^2+2u+2$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
for b=1:998
a=sqrt((b+2)^2-b^2);
if(a==floor(a))
fprintf('%d  %d  %d\n',a,b,b+2)
end
end
%以下为运行结果
4  3  5
6  8  10
8  15  17
10  24  26
12  35  37
14  48  50
16  63  65
18  80  82
20  99  101
22  120  122
24  143  145
26  168  170
28  195  197
30  224  226
32  255  257
34  288  290
36  323  325
38  360  362
40  399  401
42  440  442
44  483  485
46  528  530
48  575  577
50  624  626
52  675  677
54  728  730
56  783  785
58  840  842
60  899  901
62  960  962

4

对$c≤1000 ，c - b = k(k ≤200 )$，对哪些 $k$ 存在本原勾股数？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
for k=1:200
for b=1:999
a=sqrt((b+k)^2-b^2);
if(a==floor(a)&gcd(gcd(a,b),b+k)==1)
fprintf("%d\n",k);
break;
end
end
end
1
2
8
9
18
25
32
49
50
72
81
98
121
128
162
169
200

5

T5

$n$ $1$ $2$ $3$ $4$ $5$ $6$
$p_n$ $2$ $7$ $26$ $97$ $362$ $1351$
$q_n$ $1$ $4$ $5$ $56$ $209$ $780$
$p_n+q_n$ $3$ $11$ $41$ $153$ $571$ $2131$
$p_n+2q_n$ $4$ $15$ $56$ $209$ $780$ $2911$
$p_n-q_n$ $1$ $3$ $11$ $41$ $153$ $571$

$p_{n-1}+q_{n-1}=p_n-q_n$，$q_n=p_{n-1}+2q_{n-1}$。

所以可以推导出$p_n=2p_{n-1}+3q_{n-1},q_n=p_{n-1}+2q_{n-1}$

设$X_n=(p_n,q_n)^T$，因此将$X_n$变换到$X_{n+1}$需要用到矩阵$A=[2,3;1,2]$

SelfSkills
#Skills
MatlabExperiment1-4
http://example.com/2021/02/24/matlab1/
作者
huangx607087
发布于
2021年2月24日
许可协议