LatticeNotes6

ExpLog
CTFSeason2
发布日期:   2021-03-01

huangx607087学习格密码的笔记6

0. About

一个密码学fw的学习笔记，别看，很菜。

这个笔记并没有接着之前发布的笔记5，并且文章的tag标为Explog而不是Notes，主要讲的是LLL算法在RSA中的使用。

100天的时间，自己终于把NCTF那道题研究了出来，wtcl

1. RSA WienerAttack

我们先来回顾一下Wienerattack，Wienerattack主要是基于连分数展开，在自己的刷题记录**21Feb2[2021.2.16]**中我们提到过连分数展开的一些注意事项并进行了简单的证明以及连分数展开中精确覆盖的条件 。下面我们再来回顾一下相关的知识点：

勒让德定理：若$a \in Q, c,d\in Z,\gcd (c,d)=1$，如果有
$$
|a-\dfrac c d| < \dfrac 1 {2d^2}
$$
那么在对$a$进行连分数展开的时候，可以精确覆盖到$\dfrac c d$的值。下面我们简单证明一下WienerAttack的有效性。

设$ed = 1+kl,g=\gcd(p-1,q-1),gl=(p-1)(q-1)$，也就是说，$l$是$(p-1)(q-1)$的最小公倍数。则当$4 \ln d<\ln n$时，有：
$$
|\dfrac e n - \dfrac k {dg}|=|\dfrac 1 {dn}-\dfrac {ks}{dgn}|<\dfrac {ks}{dgn}<\dfrac 1 {2(dg)^2}
$$
那么可以通过$\dfrac e n$的连分数展开精确覆盖到$\dfrac k {dg}$。又因为$ed=k(p-1)(q-1)+1$，那么我们有
$$
edg=k(p-1)(q-1)+g,k>g
$$
因此，可以有
$$
\mathrm{floor}(\dfrac{edg}{k})=(p-1)(q-1)
$$
其中floor表示向下取整。

又因为
$$
\dfrac{pq-(p-1)(q-1)+1} 2=\dfrac {p+q} 2
$$
那么有
$$
(\dfrac{p+q}2)-pq=(\dfrac{p-q}2)^2
$$
因此我们只需要判断一下连分数中$(\dfrac{p-q} 2)^2$是否为平方数即可。附上sagemath代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#sagemath
def possible(e,alist,N): 
    for x in alist:
        if x==0:
            continue
        phi = floor(e*(1/x))
        if (N-phi+1)%2==0 and sqrt(pow((N-phi+1)//2,2)-N).is_integer():
                (p,q)=var('p,q')
                x=solve([(p-1)*(q-1)==phi, p*q==N],p,q)
                return int(str(x[0][0]).split('==')[1])
        else:
            continue
def wiener_attack(e,N):
    c=continued_fraction(e/N)
    alist=c.convergents()
    return possible(e,alist,N)
n=
e=
t=wiener_attack(e,n)
print (t)

2. Extend Wiener Attack 2D

当我们将$e$的个数从$1$提升到$2$的时候，也就是假如已知一个模数$n$和$2$个$e$值，并且这两个$e$值对应的解密指数$d$都比较小，那么我们就有了$e_id_i-k_in=1$，其中$i$取值为$1,2$。

根据我刚才得到的式子：
$$
edg=k(p-1)(q-1)+g,k>g
$$
设$s=1-p-q$，上式化简成
$$
edg-kn=g+ks
$$
那么我们就有
$$
e_1d_1g_1=g+k_1(p-1)(q-1),e_2d_2g_2=g+k_2(p-1)(q-1)
$$
然后，通过化简，消去$(p-1)(q-1)$，就有
$$
k_2d_1e_1-k_1d_2e_2=k_2-k_1
$$
然后很快就有
$$
\dfrac {e_1} {e_2}-\dfrac{k_1d_2}{k_2d_1}=\dfrac {k_2-k_1}{k_2d_1e_2}
$$
很显然，如果$2(k_2-k_1)d_1k_2<e_2$，那么我们也可以通过连分数逼近的方式，求出$\dfrac {e_1}{e_2}$连分数展开中的精确覆盖的值$\dfrac{d_2k_1}{d_1k_2}$，但着想找到$d_1,d_2$时基本不现实的。

那么这就进入了Extend Wiener Attack

根据构造格进行LLL的要求，我们必须要确定已知量和未知量。在这里已知量是$e,n$，未知量是$k,d,s,g$，

那么根据我们刚刚构造的式子：
$$
k_2d_1e_1g-k_1d_2e_2g=k_2g-k_1g[1]
$$

$$
d_1gk_2e_1-k_1k_2n=k_2g+k_1k_2(pq-p-q+1)=k_2g+k_1k_2s[2]
$$

$$
(e_1d_1g-k_1n)(e_2d_2g-k_2n)=(g+k_1s)(g+k_2s)[3]
$$

$[3]$可以继续进行化简，得到：
$$
d_1d_2g^2e_1e_2-d_1gk_2e_1n-d_2gk_1e_2n+k_1k_2n^2=(g+k_1s)(g+k_2s)[3]
$$
然后我们考虑一下构造矩阵：由于等号最左边最大长度是$4$，因此需要构造一个$\mathrm{4x4}$的矩阵。因此我们要考虑凑个数。我们发现：$[2][3]$中都有$k_1k_2$这个元素，因此我们可以凑一个$k_1k_2$出来。

因此，根据$\vec vA=\vec w$构造法则，我们可以构造：$\vec v=(k_1k_2,k_2d_1g,k_1d_2g,d_1d_2g^2)$，$\vec w=(k_1k_2,k_2g-k_1g,k_2g+k_1k_2s,(g+k_1s)(g+k_2s))$，这样使得向量$\vec v$和向量$\vec w$包括了所有的未知量。然后就可以构造已知量矩阵$A$如下图了。

1

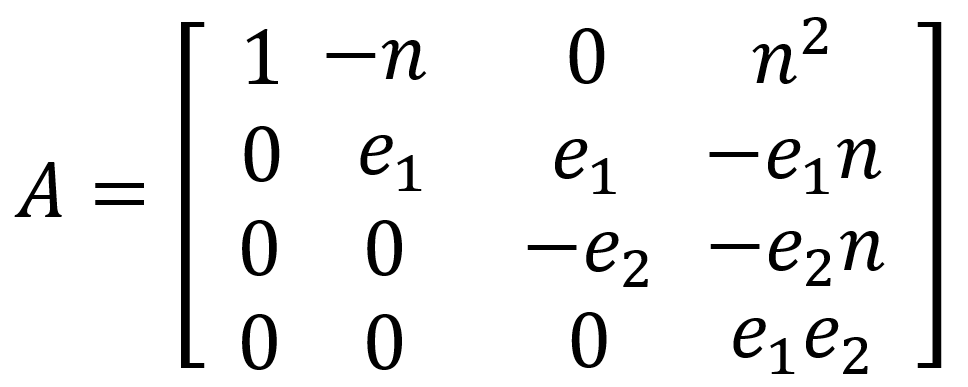
这里是四维的矩阵，很显然其行列式的值为$ne_1e_2^2$。但向量$\vec w$的长度明显要长很多。因此我们就开始考虑扩大$\det A$的值。

根据我们已知条件，有$e≈n,k≈d≈n^b,g≈1,s≈\sqrt n$。因此，$\det A ≈ n^4$，而$|\vec w|$明显大于这个数。这个时候我们就可以他通过对矩阵得列乘上一个数得倍数使得条件满足。

这个时候，我们就可以给矩阵第一列乘上$n$，第二列乘上$\sqrt n$，第三列乘上$n^{1+b}$使得条件满足，这也就是通过矩阵的列乘上一个数字使得条件满足。

因此，构造后的$\vec w$为
$$
\vec w=(k_1k_2n,k_2g-k_1g\sqrt{n},k_2g+k_1k_2sn^{1+b},(g+k_1s)(g+k_2s))
$$
此时可以计算出$|\vec w|< 2n^{1+2b}$，也就是
$$
2\sqrt[4]{\det A}=2n \sqrt[8]{13+2b}
$$
然后有$b≤\dfrac 5 {14}$。然后可以带入$n^{1+b}$中，然后对$A$使用$LLL$算法求出$A$的最短向量$\vec w$，然后计算$\vec v =\vec w A^{-1}$，利用$A$的前两项求出$\phi=(p-1)(q-1)$，这里有$\phi=e_1 \dfrac {k_1k_2}{k_2d_1g}$。

3.例题 [2020羊城杯] Simple

首先看一下题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from Crypto.Util.number import *
from Crypto.Cipher import DES
import gmpy2
from secret import flag
import random
key = "abcdefgh"
def des_encrypt(m):
    des = DES.new(key, DES.MODE_ECB)
    res = des.encrypt(m)
    return res
def gen_key():
    p = getPrime(2048)
    q = getPrime(2048)
    n = p * q
    bit = n.bit_length()
    phi_n = (p - 1) * (q - 1)
    num = random.randint(1, 100)
    while True:
        u = getPrime(bit / 4 - num)
        if gmpy2.gcd(u, phi_n) != 1:
            continue
        t = gmpy2.invert(u, phi_n)
        e = bytes_to_long(des_encrypt(long_to_bytes(t)))
        if gmpy2.gcd(e, phi_n) == 1:
            break
    return (n, e)
P = getPrime(1024)
Q = getPrime(1024)
N = P * Q
E = 65537
lcm = gmpy2.lcm(P-1, Q-1)
e1 = gmpy2.invert(getPrime(730), lcm)
e2 = gmpy2.invert(getPrime(730), lcm)
m = bytes_to_long(flag)
c = pow(m, E, N)
print "N = " + str(N)
print "e2 = " + str(e2)
print "C = " + str(c)  
_n, _e = gen_key()
_c = pow(e1, _e, _n)
print "n = " + str(_n)
print "e = " + str(_e)
print "c = " + str(_c)

整个题目可以分为两部分解决。我们首先可以通过一次DES解密可以获得$t$值。注意到$ut\equiv 1 \pmod {phin}$，而$4\ln u<\ln t$，因此我们可以直接通过wiener attack求出$u$的值。进而就可以解密出$e_1$的值了。其中求$u$得值就用的上面得WienerAttack脚本。

1
2
3
4
5
6
7
8
9
from Crypto.Util.number import *
from Crypto.Cipher import DES
from given import *
des=DES.new(b"abcdefgh",DES.MODE_ECB)
t=bytes_to_long(des.decrypt(long_to_bytes(e)))
u=11797660359487393794703501696733722234597800563221644744216546283873417801358839752749644652587148151353963016872894291750625278074742782471171817895256720486745393451876158473621006168530167397313514152556156473219068407536794185608357374065375644916773016430063167943099951326297693
phi=(t*u-1)
d=inverse(e,t*u-1)
e1=(pow(c,d,n))

然后我们就可以发动Extend Wiener Attack，可以注意到这里两个未知的素数都在$730$位，因此我们就有$b=730$，$n$是$2048$位。直接根据刚才的理论构建格矩阵即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#Sagemath
from Crypto.Util.number import *
c=...
n=...
e1=...
e2=...
M=[[1,-n,0,n*n],[0,e1,e1,-e1*n],[0,0,-e2,-e2*n],[0,0,0,e1*e2]]
S1,S2=int(n^0.5),int(n^(1+730/2048))
D=diagonal_matrix(ZZ,[n,S1,S2,1])
M=matrix(ZZ,M)*D
w=vector(ZZ,(M).LLL()[0])
v=w*M^(-1)
phi = int(v[1]//v[0]*e1)
d=inverse(65537,phi)
m=pow(c,d,N)
print (long_to_bytes(m))
#b'GWHT{3da44ca8379b98fdc1c86f9b34dcc1ef}'

4. 3D & 4D Expand WienerAttack

实际上，我们如果比较一下上面的值，可以发现$\ln d = 0.35 \ln n$，超过了我们之前说过的$0.25$的比值。而实际上，随着格维度的增加(普通的WienerAttack可以认为是一维的)，允许的$\ln d$与$\ln n$的比值也在增加。下面是$n=1$到$7$时Expand Wiener Attack 所允许的最大比值，最高可以到$0.5$。

$n$ $1$ $2$ $3$ $4$ $5$ $6$ $≥7$
$\dfrac{\ln d}{\ln n}$ $0.25$ $0.357$ $0.4$ $0.441$ $0.468$ $0.493$ $0.5$

而实际上，我们通过观察之前二维的格的值，会发现推导时经常用到两个式子，下面我们为了简化，给这两个常用式子打个tag：
$$
[W_1]:e_1d_1g-k_1n=g+k_1s
$$

$$
[G_{(12)}]:e_2e_2k_1-e_1d_1k_2=k_2-k_1
$$

在二维的格中，我们假设格基本单位为$A$，行变换对角矩阵为$P$，列变换对角矩阵为$Q$，那么在刚才二维的格中，$A_2$的值入下图

2

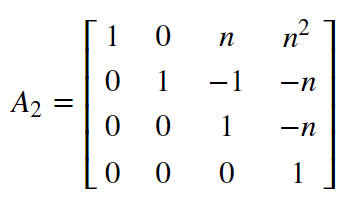
而$P_2=\mathrm{diag}(1,e_1,e_2,e_1e_2),Q_2=\mathrm{diag}(n,n^{0.5},n^{1+b},1)$。其中$b$是我们估计的$\dfrac{\ln d}{\ln n}$的值。

并且不要忘记$\vec v_2=(k_1k_2,d_1k_2g,k_1d_2g,d_1d_2g^2)$。

下面我我们尝试构建一下三维的情形：

首先是类比$\vec v$的值，由于三维的出现了$k_3$，因此$\vec v$中每个分量的$k$和$d$的值个数之和应该为$3$。并且注意到$\vec v$中的一个分量有几个$d$，对应的那个分量就要乘上$g$的几次方，因此，我们可以构造出
$$
\vec v_3=(k_1k_2k_3,d_1k_2k_3g,k_1d_2k_3g,d_1d_2k_3g^2,k_1k_2d_3g,d_1k_2d_3g^2,k_1d_2d_3g^2,d_1d_2d_3g^3)
$$
可以看出$\vec v_3$的前三个分量仅仅是把$\vec v_2$中的所有分量都乘上了个$k_3$，因此，如果$A_3$看作分块矩阵的话，$A_3$的左上角应当是$A_2$，左下角应当是$0$矩阵。同理，我们还可以类比出$A_3$的第五列和第八列的值，参考一下表达式$G_{13}$和表达式$W_1W_2W_3$即可。

不过，如果我们想构建含有$d_1d_3$的表达式（并且还不能有$d_2d_3$项出现）考虑到这一结构，我们可以构建$W_1G_{23}$来解决。不过最后为保证$g$的指数足够需要乘上一个$g$。同理，构建含有$d_2d_3$的表达式，那就设置$W_2G_{13}$解决。

因此，我们构建的格$A_3$如下，其中第$5,8$两列可以类比一下得到，$6,7$两列通过通过$W,G$两个式子的组合来完成。

3

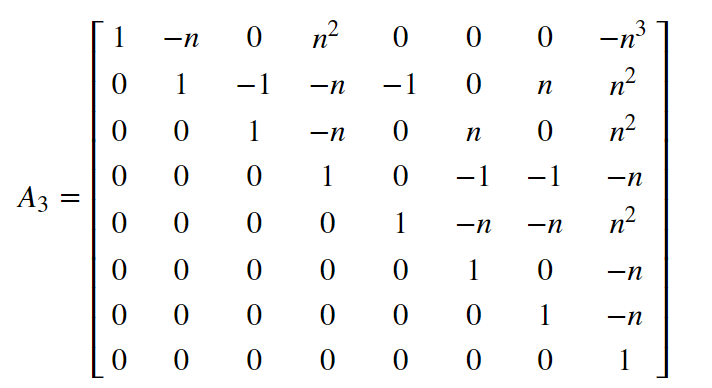
那么，我们可以获得列$1$到$8$的原始推导式

$1$ $2$ $3$ $4$
$k_1k_2k_3$ $W_1k_2k_3$ $G_{12}k_3g$ $W_1W_2k_3$
$5$ $6$ $7$ $8$
$k_2G_{13}$ $W_1G_{23}g$ $W_{2}G_{13}g$ $W_1W_2W_3$

其中如果推导时发现$g$的指数不足，需要补$g$的指数，上面第$3,6,7$个推导式就是如此

类比$P_{3}$，我们通过二进制思维，可以很容易地由$P_2$构建出
$$
P_3=\mathrm{diag}(1,e_1,e_2,e_1e_2,e_3,e_1e_3,e_2e_3,e_1e_2e_3)
$$
不过$Q_3$就不是那么好构造了。我们还是假设$b=\dfrac{\ln d}{\ln n}$。

那么有$k_1k_2k_3s^3≈n^{3(b+0.5)}$，因此我们发现，当格的维数提升$1$时，观察矩阵$P_3A_3$每一列最上面的非$0$元那么对应的分量就要提升$0.5$，如果某一列对应的最高非零元出现了$e$，指数还需要附加一个$b$。而如果最高非零元$n$的指数每增加$1$，那么$Q$对应分量$n$的指数就降低$0.5$。

因此我们可以i继续构造表格：

列数$i$ $1$ $2$ $3$ $4$
最高非$0$元 $1$ $-n$ $-e_1$ $n^2$
$Q_{ii}$ $n^{1.5}$ $n$ $n^{1.5+b}$ $n^{0.5}$
列数$i$ $5$ $6$ $7$ $8$
最高非$0$元 $-e_1$ $e_2n$ $e_1n$ $-n^3$
$Q_$ $n^{1.5+b}$ $n^{1+b}$ $n^{1+b}$ $1$

$$
Q_3=\mathrm{diag}(n^{1.5},n,n^{1.5+b},n^{0.5},n^{1.5+b},n^{1+b},n^{1+b},1)
$$

这样子的话，我们三维的情况就构造好了，三维可以解决$\ln d=0.4\ln n$的情形。

后面就是考虑构建四维的格。很显然，在四维的格里面，$\vec v_4$中每个分量含$d$的个数分别是从$1$到$4$。其中通过类比$\vec v_3$中给了我们构造分量中含$0,1,2$个$d$的方法，并且最后全是$d$的情况的是所有$W$式相乘。因此，我们就需要考虑考虑$3$个$d$的构造方法。

由于我们只有$W$式和$G$式，如果想要让式子中有$3$个$d$，其中必须要包含$d_4$，以构造$\vec v_4$中的第$12$个分量$d_1d_2k_3d_4g^3$的情况为例，我们需要的是$d_1d_2$，并且不能出现$d_3d_4$的乘积得到情况，那么我们可以直接乘上$W_1W_2$。而如果我们想分开$d_3,d_4$,那就可以给过去一个$G_{34}$，通过构造$G_{34}W_1W_2$来完成。

因此，我们可以直接得到$A_4$矩阵，也可以类比出$P_4,Q_4$

4
$$
P_4=\mathrm{diag}(1,e_1,e_2,e_1e_2,e_3,e_1e_3,e_2e_3,e_1e_2e_3,e_4,e_1e_4,e_2e_4,e_1e_2e_4,e_3e_4,e_1e_3e_4,e_2e_3e_4,e_1e_2e_3e_4)
$$

$$
Q_4=\mathrm{diag}(n^2,n^{1.5},n^{2+b},n,n^{2+b},n^{1.5+b},n^{1.5+b},n^{0.5},n^{2+b},n^{1.5+b},n^{1.5+b},n^{1+b},n^{1.5+b},n^{1+b},n^{1+b},1)
$$

当然，我们还可以扩展到$5,6,7$维的情况，这里就不再赘述。

5.例题 [2020NCTF] RRRSA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#RSA.py
from Crypto.Util.number import getPrime, getRandomNBitInteger, GCD, inverse
lcm = lambda x, y: x*y // GCD(x,y)
class RSA():
    def __init__(self, bits):
        p = getPrime(bits//2)
        q = getPrime(bits//2)
        self.N = p * q
        self.lbd = lcm(p-1, q-1)
        self.gen_ed(bits)
    def gen_ed(self, bits):
        while True:
            d = getRandomNBitInteger(int(bits*0.4))
            if GCD(d, self.lbd) == 1:
                e = inverse(d, self.lbd)
                self.e, self.d = e, d
                break
    def encrypt(self, m):
        return pow(m, self.e, self.N)
    def decrypt(self, c, d):
        return pow(c, d, self.N)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#task.py
from random import choice
from hashlib import sha256
from string import ascii_letters, digits
from RSA import RSA
from secret import FLAG
MENU = """
1. encrypt
2. decrypt
3. newkey
4. encflag
5. exit"""
def proof_of_work():
    proof = ''.join([choice(ascii_letters+digits) for _ in range(20)])
    _hexdigest = sha256(proof.encode()).hexdigest()
    print(f"sha256(XXXX+{proof[4:]}) == {_hexdigest}")
    try:
        prefix = input("Give me XXXX: ")
    except:
        print("Error!")
        exit(-1)
    return sha256((prefix+proof[4:]).encode()).hexdigest() == _hexdigest
def task():
    CHANCE = 1
    RRRSA = RSA(1024)
    print(f"My public key: {RRRSA.e}, {RRRSA.N}")
    for _ in range(10):
        try:
            print(MENU)
            choice = input("Your choice: ")
            if choice == "1":
                m = int(input("Your message: "))
                c = RRRSA.encrypt(m)
                print(f"Your cipher: {c}")
            elif choice == "2":
                c = int(input("Your message: "))
                d = int(input("Your decryption exponent: "))
                m = RRRSA.decrypt(c, d)
                print(f"Your message: {m}")
            elif choice == "3":
                RRRSA.gen_ed(1024)
                print(f"My new public key: {RRRSA.e}, {RRRSA.N}")
            elif choice == "4":
                if CHANCE:
                    CHANCE -= 1
                    flag = int.from_bytes(FLAG, 'big')
                    encflag = RRRSA.encrypt(flag)
                    print(f"encflag: {encflag}")
                else:
                    print("Nope, only 1 chance to get encflag.")
            else:
                print("Bye!")
                exit(0)
        except Exception as e:
            print(e)
            print("Error!")
            exit(-1)
if __name__ == "__main__":
    if proof_of_work():
        task()

通过观察代码，可以看到：每次生成的$d$满足$\ln d = 0.4 \ln n$的规模。而$n$得值自始至终都是不变化的，但与普通的共模攻击不同的就是，我们只能获得一次flag的密文。因此可以使用Extend WienerAttack。而根据这边$b=0.4$的规模，就构造$4$维的格

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
from Crypto.Util.number import *
n=
e=
c=
e1=
e2=
e3=
e4=
A=[
[1,-n,0,n^2,0,0,0,-n^3,0,0,0,0,0,0,0,n^4],
[0,1,-1,-n,-1,0,n,n^2,-1,0,n,0,n,0,-n^2,-n^3],
[0,0,1,-n,0,n,0,n^2,0,n,0,0,0,-n^2,0,-n^3],
[0,0,0,1,0,-1,-1,-n,0,-1,-1,0,0,n,n,n^2],
[0,0,0,0,1,-n,-n,n^2,0,0,0,-n^2,0,0,0,-n^3],
[0,0,0,0,0,1,0,-n,0,0,0,n,-1,0,n,n^2],
[0,0,0,0,0,0,1,-n,0,0,0,n,0,n,0,n^2],
[0,0,0,0,0,0,0,1,0,0,0,-1,0,-1,-1,-n],
[0,0,0,0,0,0,0,0,1,-n,-n,n^2,-n,n^2,n^2,-n^3],
[0,0,0,0,0,0,0,0,0,1,0,-n,0,-n,0,n^2],
[0,0,0,0,0,0,0,0,0,0,1,-n,0,0,-n,n^2],
[0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,-n],
[0,0,0,0,0,0,0,0,0,0,0,0,1,-n,-n,n^2],
[0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,-n],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,-n],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1]]
Q=[n^2,n^1.5,n^2.4,n,n^2.4,n^1.9,n^1.9,n^0.5,n^2.4,n^1.9,n^1.9,n^1.4,n^1.9,n^1.4,n^1.4,1]
P=[1,e1,e2,e1*e2,e3,e1*e3,e2*e3,e1*e2*e3,e4,e1*e4,e2*e4,e1*e2*e4,e3*e4,e1*e3*e4,e2*e3*e4,e1*e2*e3*e4]
A,P,Q=matrix(ZZ,A),diagonal_matrix(ZZ,P),diagonal_matrix(ZZ,Q)
A=P*A*Q
w=vector(ZZ,A.LLL()[0])
v=w*A^(-1)
phi=int(e1*v[1]//v[0])
print(hex(phi))
d=inverse(e,phi)
print(long_to_bytes(pow(c,d,n)))
#NCTF{Aft3r_411__t0morr0w_1s_an0ther_d4y}

当然也可以构造三维的格，不过这里边界卡的比较死(恰好$0.4$左右)，可能会导致不稳定，需要多试几次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from Crypto.Util.number import *
e=
c= 
e2= 
e1= 
n= 
e3=
A=[[1,-n,0,n^2,0,0,0,-n^3],
[0,1,-1,-n,-1,0,n,n^2],
[0,0,1,-n,0,n,0,n^2],
[0,0,0,1,0,-1,-1,-n],
[0,0,0,0,1,-n,-n,n^2],
[0,0,0,0,0,1,0,-n],
[0,0,0,0,0,0,1,-n],
[0,0,0,0,0,0,0,1]]
P=[1,e1,e2,e1*e2,e3,e1*e3,e2*e3,e1*e2*e3]
Q=[n^1.5,n,n^1.9,n^0.5,n^1.9,n^1.4,n^1.4,1]
A,P,Q=matrix(ZZ,A),diagonal_matrix(ZZ,P),diagonal_matrix(ZZ,Q)
A=P*A*Q
w=vector(ZZ,A.LLL()[0])
v=w*A^(-1)
phi1,phi2=int(e1*v[1]//v[0]),int(e2*v[2]//v[0])
phi=int(phi1)
print(hex(phi1))
d,d0=inverse(e,phi),inverse(e2,phi)
print(long_to_bytes(pow(c,d,n)))

6.总结

RSA与格密码的结合，还是比较难的（，自己NCTF在放题后100天，本地复现的时候才做出来（（（

文章作者: huangx607087
文章链接: http://example.com/2021/03/01/LatticeNotes6/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 huangx607087 !
ExpLog
赏
  目录