An Interesting Problem-RSAOS

ExpLog
CTFSeason3
发布日期:   2021-07-15

An Interesting Problem - RSAOS

0.About

最近自己在BUU上面刷题的时候发现了一个很好玩的题目——RSAOS，虽然本fw还是瞄了几眼WP才写出来的——因为自己tcl，但还是决定跟大家分享一下——因为确实非常的好玩

7月14日，BUUCTF上了5000分，以后还要继续努力。

#define huangx607087 fw

Part 1 Beginning

1

题目什么附件都没有给，就是一个普普通通的远程题目，直接打开虚拟机远程连接上去（

然后远程连接上去之后，似乎什么东西都没有（，并没有让你输出什么sha256验证的，也没有输出什么RSA必要的$c,e,n$的必要解密条件。随便输入一个e，n，ls之类的东西都显示”Commond Not Found”。。。。。。

2

这就是一个很奇怪的玩意了——不仅没有源码，还没给什么其他的东西（

于是本fw毫不要脸地去瞄了一眼这道题的wp，原来第一步要先输入help获取菜单——行吧，怪我自己没有开发经验，谁叫自己是一个连机器人都配不好的fw呢?下亿次我拿到一个未知的系统一定要先输一下help或者menu等功能性命令，（拿小本本记下来

输入了help之后，似乎很多事情就好起来了（，得到了一连串的命令——

3

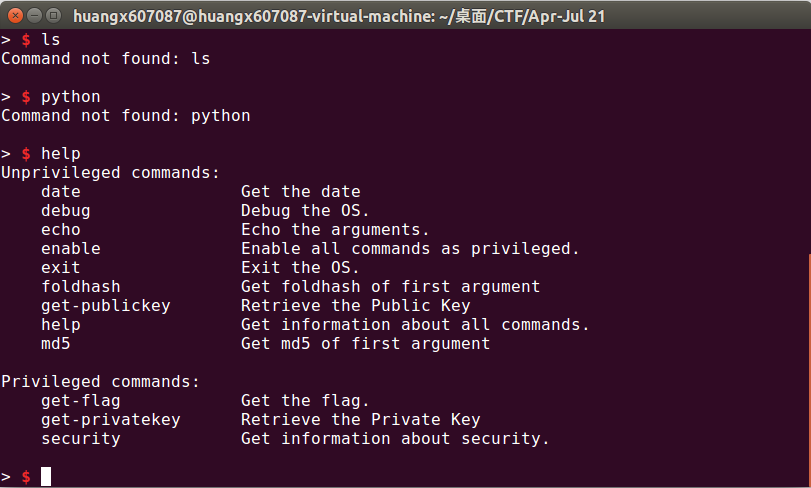
Part 2 Attempt 1

乱搞阶段

很显然，要输入get-flag或者get-privatekey，我们才能获得最终答案。因此先输一下get-flag来看看需要什么条件（

4

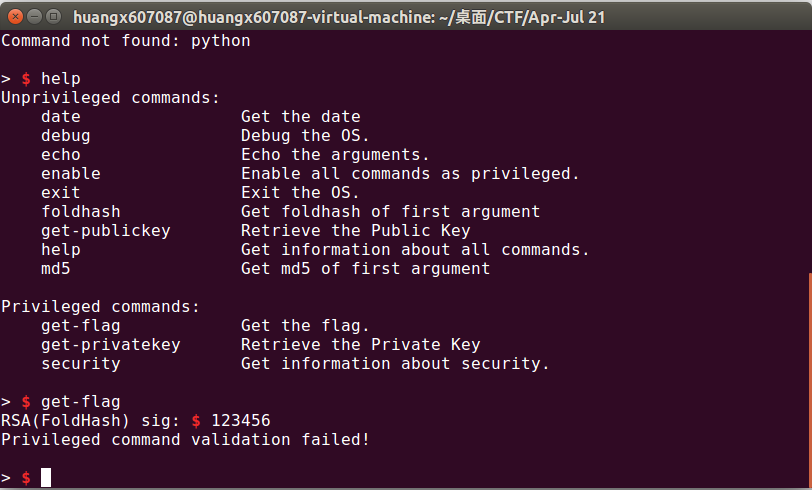
然后它给我冒出来了一个什么foldhash的东西（看来这玩意还是有点东西的。可能权限命令需要某个密码才能完成吧——要记住这是Crypto题目不是Pwn/Re题目，估计其他的内容不会很难

输入get-publickey，服务器返回了这样一个东西：貌似重连几遍内容一直不变

1
2
3
Public key parameters:
N: 0xd888075370effdb016d85de8c894ee7ac2764527210d8ce1d8bd14a06c67de148b4680781366002f9649e3885e18ab950120c660970ab9a499ea74ea7aa38fe732940b5204300ef7b96a608efec1a74007a4b1d592cf9eb23890d8fa416202857d0e0f9ebad79324d03d09db0502ff4bae0b2dfc0b150ddea806a5ff24e2d32f
E: 0x10001

duck不必管那么多，或许其他的东西应该试试看（，比如没试过的命令都尝试日一遍看看（，尤其是这个debug，我看你很不对劲[严肃]

5

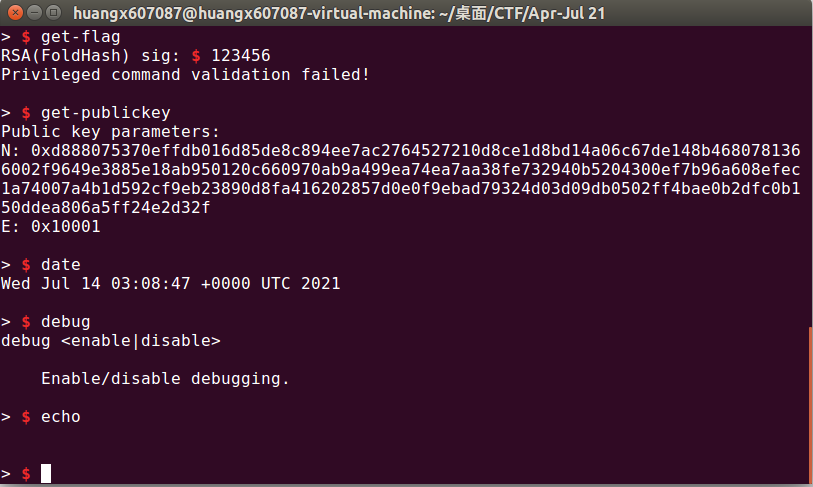
果然debug这边确实有什么玄机在里面！或许我们应当enable一下这个debug才对

6

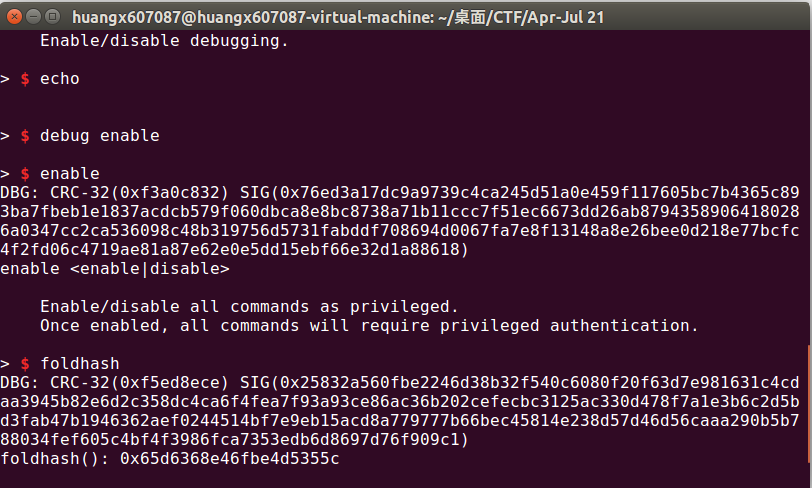
果然在debug enable之后，似乎每次输出命令都会给你一个什么DBG-CRC32() SIG()的模式。不过这个究竟是什么东西啊（

百度了一下，原来CRC32()是一个$32$个比特位的哈希值，而SIG是签名结果。

不过这个时候自己的发展又陷入僵局。。。。（于是再一次瞄了眼别人的wp）

结果发现这是个脑洞题——原来help后面还可以跟上命令名称来告诉你这个命令究竟是干什么用的

7

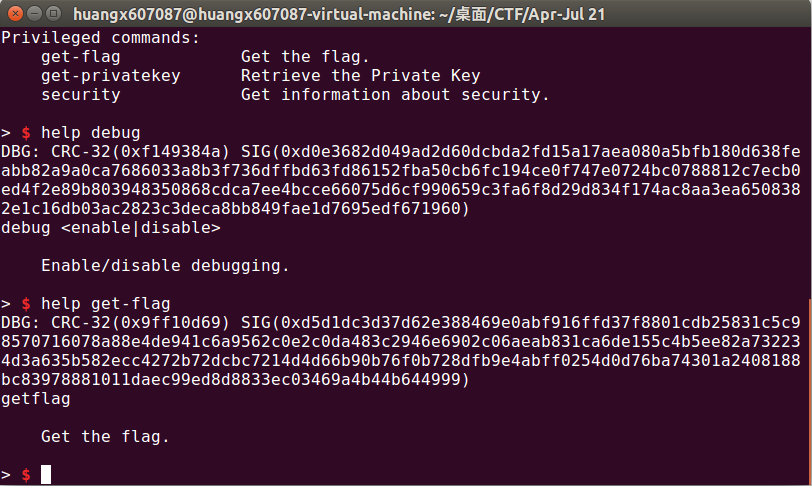
在help security这边，我们发现了比较有价值的信息：

8

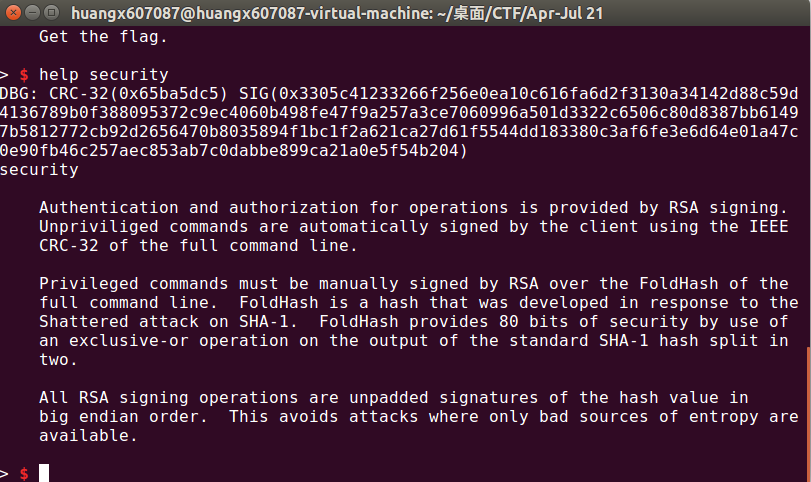
简单翻译一下并概括，差不多是这两条内容：

1
2
3
1.非特权命令的签名内容是对你输入内容的CRC32进行签名，而特权命令的签名内容是其FoldHash进行签名的内容
2.FoldHash是通过输入内容sha1获得的160个比特位的前80个和后80比特位异或后得到的结果
3.每次给出的签名和CRC32的值是一整行的内容，如果命令中有空格，那么最后实际执行的内容仅仅是第一个命令(argument)

经过查询，CRC32是一种hash方法，其hash后取值范围是$0$到$2^{32}-1$，该方法哈希冲突率比较高。

Part 3 Analyzation

于是乱搞到这里差不多可以结束了（，得正式地做题了（

首先先来回顾一下一下RSA的数字签名

签名方式：
$$
\mathrm{SIG}(x)\equiv x^d \pmod n
$$
验证方式：
$$
\mathrm{Verify}(x)\equiv \mathrm{SIG}^e(x)\pmod n
$$
很显然，用于验证的内容时私钥。因此我们需要尝试伪造一个签名才可以完成。

根据题目提示，不难分析出其foldhash的原理。

1
2
3
4
5
6
#Sagemath
def foldhash(s):
    s=sha1(s.encode()).digest()
    a,b=bytes_to_long(s[:10]),bytes_to_long(s[10:])
    return a^^b
# Different from Python: in Sagemath, ^^ means xor and ^ means power

关注到foldhash实际上是一个数字，CRC32也是一个数字，只不过foldhash的比特位是$80$，而CRC32的结果是$32$位。如果使用特权命令，那么你需要搞出你输入的那一行内容的数字签名。

注意到上面分析的第三条，暗示着我们可以在特权命令后面加一下东西，我们就可以获取到必要的特权命令foldhash的签名了，也就是特权命令的$\mathrm{foldhash}(x)\equiv x^d \pmod n$的值。

不过我们这边有个问题来了：$x$是$80$位的内容，但CRC32最后是$32$位内容，因此我们需要构造一个字符串，其格式为"get-flag "+padding，使得该字符串的foldhash值满足$\mathrm{FFFFFFFFH}$光滑，最后根据RSA的同态性将所有SIG值相乘后就是我们需要的内容了

果然，瞄了一眼WP，WP也是这么写的，不过他直接用的get-flag 0，该命令的foldhash的值为$637185588446528046742504$。其分解质因数结果为：
$$
637185588446528046742504=2^3×250091×244079963×1304805461
$$
不过直接抄wp肯定是没意思的，但问题是这个get-flag 0真的这么好构造出来吗？于是我在Sagemath中测试了以下代码，随机在字符串get flag 后面填充$8$位十六进制数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#Sagemath
from Crypto.Util.number import *
from hashlib import sha1
from random import *
def foldhash(s):
    s=sha1(s.encode()).digest()
    a,b=bytes_to_long(s[:10]),bytes_to_long(s[10:])
    return a^^b
def padding(s,n):
    TABLE="abcdef0123456789"
    t=" "
    for i in range(n):
        t+=choice(TABLE)
    return s+t
NUMBERS=0
while 1:
    NUMBERS+=1
    s=padding("get-flag",8)
    q=foldhash(s)
    li=list(factor(q))
    if(li[-1][0]<=0xffffffff):
        print(s)
        print(q)
        print(li)
        print(NUMBERS)
        break

下图是一次运行结果。

9

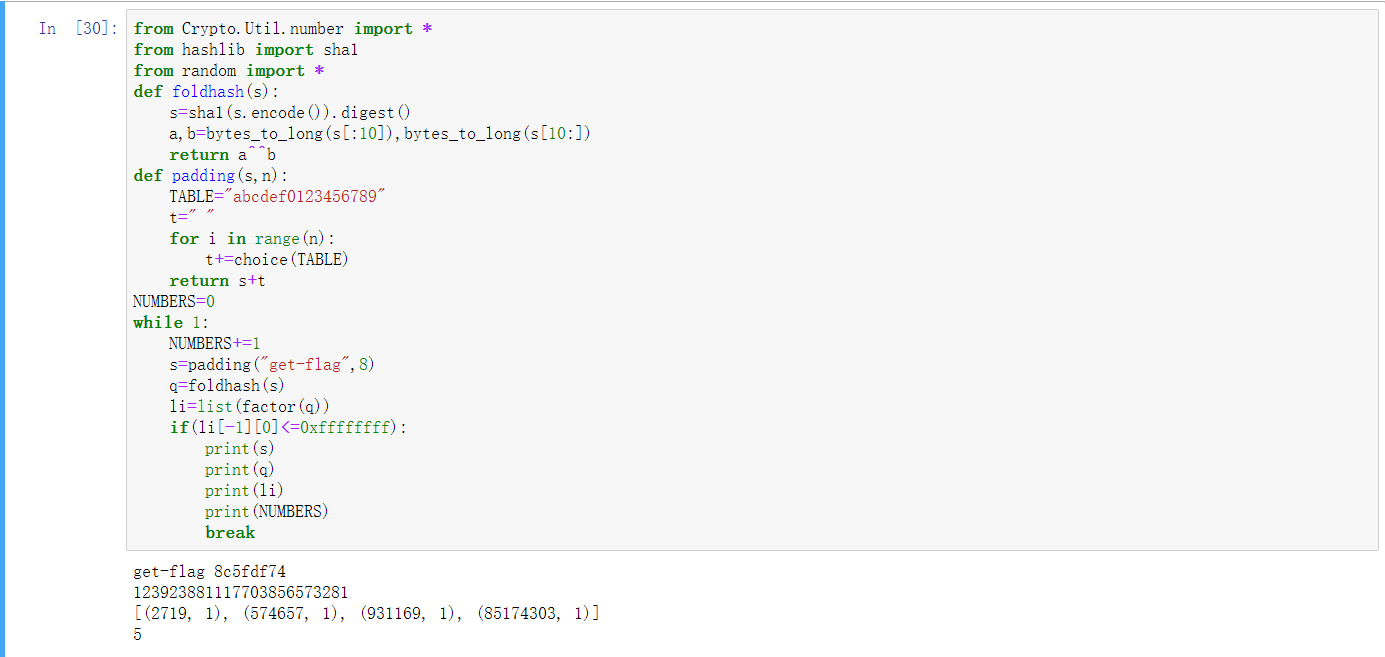
于是我构造了一个不同并且更简单的字符串：get-flag 8c5fdf74，其foldhash值为$123923881117703856573281$，质因数分解结果为$2719×574657×931169×85174303$，随机生成了$5$次后得到了这个结果。

然后我又重复运行了这个代码数次，发现最多的一次为$21$次尝试获得符合条件的字符串，最少一次可以一发命中符合条件的字符串，平均大概$6$到$7$次左右的尝试即可产生符合条件的字符串——说明符合条件的字符串并不难找。

于是找字符串这个问题就这样解决了。下面就是寻找$4$个符合条件的字符串$s_1,s_2,s_3,s_4$，让其CRC32值分别为$2719,574657,931169,85174303$——看来这似乎是一个有难度的事情。

实际上枚举$6$位内容的可见字符串在原则上是可行的。不过github上还是能找到一个包（[戳这里](theonlypwner/crc32: CRC32 tools: reverse, undo/rewind, and calculate hashes (github.com))），直接下载即可。

Part 4 Attempt 2

真正的尝试阶段

阅读过这个包的内容后，开始了尝试。

10

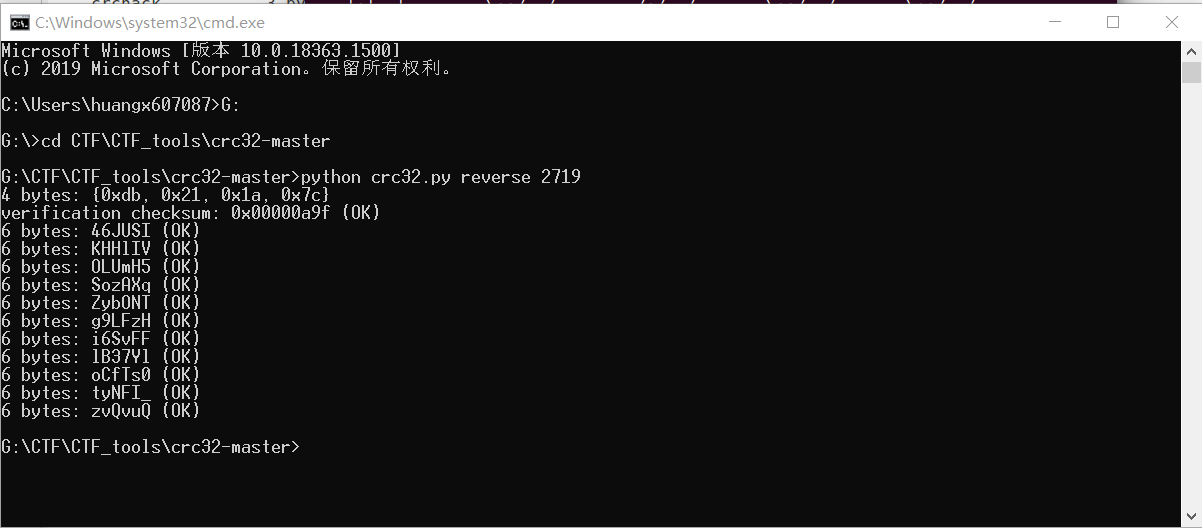
然后我连续发送了三个过去，结果发现不对（，那边的验证结果是0xe0db37ee。这两个内容之间是不是有什么联系在里面啊（

11

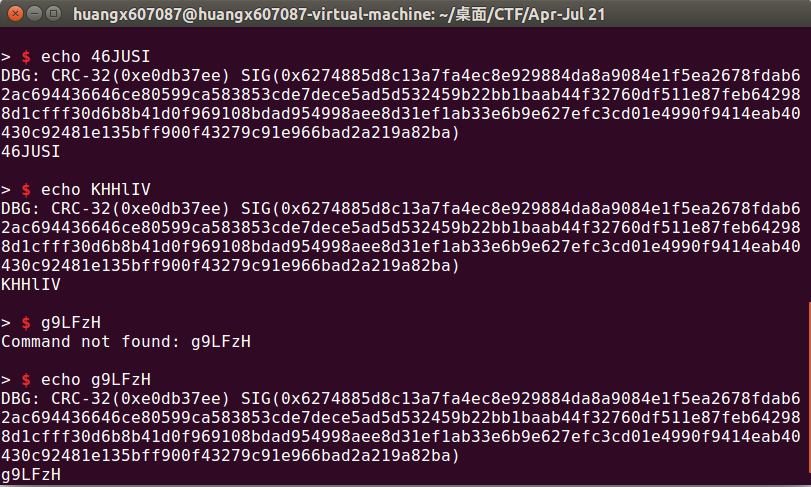
那我找个0xe0db37ee的值发过去试试看呢？

12

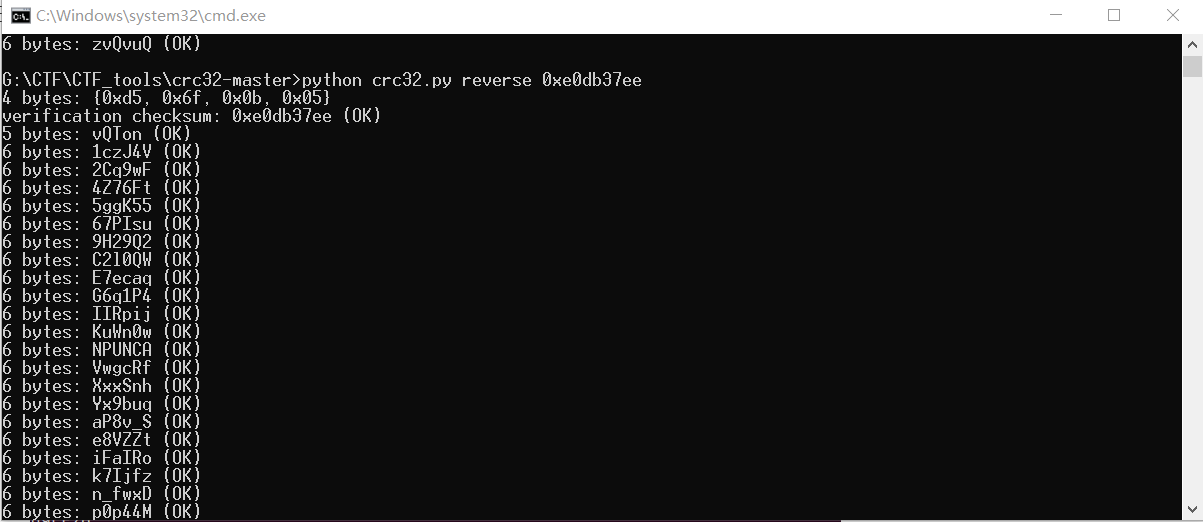
果然，最后的结果是正确的，此时记录下签名结果

13

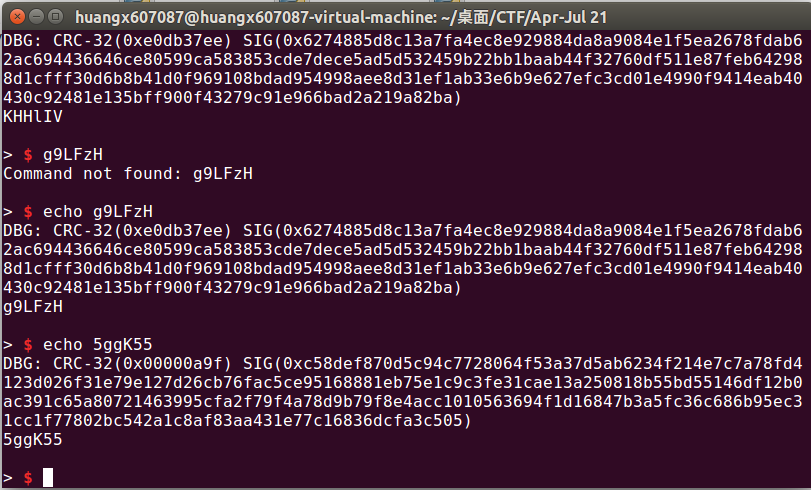
于是重复上面的步骤，我们就可以获得另外三个的内容了（

14

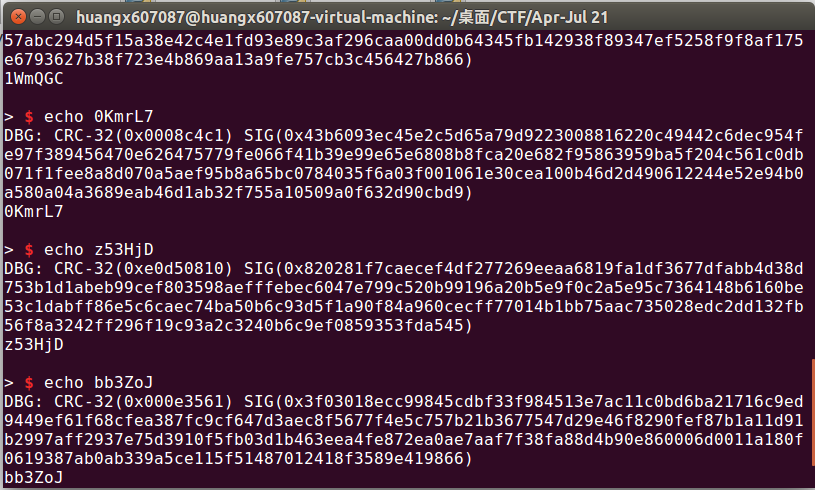
将得到的$4$个SIG乘起来模$n$，获得最终的结果。发送过去得到flag。

15

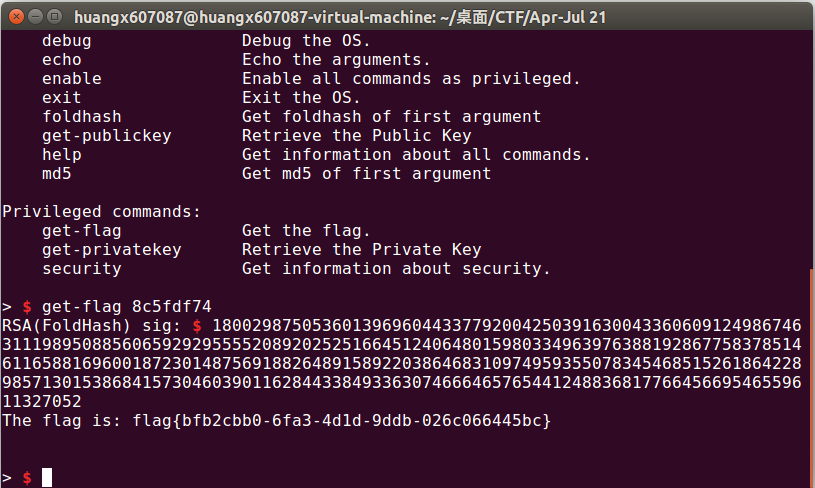
5.More Exploration

搞出来flag之后，本fw很形象再去看看另外两个命令是干什么的，于是决定如法炮制伪造字符串

我们可以使用的字符串如下：

16

根据上面的内容可以获得其私钥：

1
2
3
4
5
N: 0xd888075370effdb016d85de8c894ee7ac2764527210d8ce1d8bd14a06c67de148b4680781366002f9649e3885e18ab950120c660970ab9a499ea74ea7aa38fe732940b5204300ef7b96a608efec1a74007a4b1d592cf9eb23890d8fa416202857d0e0f9ebad79324d03d09db0502ff4bae0b2dfc0b150ddea806a5ff24e2d32f
E: 0x10001
P: 0xf0d4aa4868305cdbabba679014f940c0233ca0b10c9db62e3d829dd289103b21143da614b361c6043711956ff2ffd3bf7dcea0418a1e0bbf74784512f99733cd
Q: 0xe62b8ad7f10d9921a3be7b0c74a81107b5fa704900f94028c6a6e401a00729f6ed961dabbc65878ba5b7f34ca406c7b27577fe5153909d036ecf7e028b555eeb
D: 0x77de15f0233d37fb1b2a7c1239b7f8ad0ca9dc6e64e5d36fd34418ff160409f4e58509e96f13b056a7a40fc9960da22ec2891a48ae54c9a04d747574b89f83313d1902224cb7e90bf74a30a6e0201e3081c33ea14786adec8f7e05c898f9f55c7e332f7cc7a12263eac1ae60e2122e548207fe3c035e03eaf36798c62c3f6e41

而security命令的输出与help-security的输出一模一样。。。

6.Review

一道很好玩的题目还是值得把玩以下的，感觉收获很大。

最后附一下网上给的CRC32加密原理，以后研究。

17 18
文章作者: huangx607087
文章链接: http://example.com/2021/07/15/An-Interesting-Problem-RSAOS/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 huangx607087 !
ExpLog
赏
  目录