Lattice Notes 7

huangx607087对构造格及多项式的笔记 7

0.简介

之前遇到过很多以及近期遇到过的几个CTF题目中，都出现了需要构造格或者多项式求小根的题目，在这里分享一下以备用。

注：由于博客技术限制，一些复杂指数的表达式呈现容易出现错误。故本博客中部分指数表示方法改用对数$\ln$表示。

一般情况下，如果题目中给出了未知量组$x_s$与已知量$a_t$的关系，以及总模数为$n$。如果出现大约$4\ln x<\ln n$，且可以构造出矩阵$A$和行向量$\vec X$。其中$A$中只含有已知数，$\vec X$中包含了所有的未知数，且可以确定既定的关系$\vec XA=\vec Y$，那么这道题就可以考虑构造格来解决。

简而言之，就是题目中出现了非常小未知数与非常大

而将问题退化一个层次，我们可以通过Coppersmith定理来获取有限域内多项式的小根。

Coppersmith定理：在定义域为$Z_n$的$e$阶多项式$f(x)$中，如果有一个根$x$满足$e\ln x<\ln n$ ，就可以运用一个$O(\ln n)$的算法求出这些根。

Update 2021.8.2 增加了一些关于ECC的解题方法

1.几种简单的构造多项式的情况

1o01 已知明文高位

假设在RSA传播过程中造成$m$的高位泄露，如果$e$是$3$，假设已知部分是$m_0$，未知部分是$x$，满足$m=m_0+x$且$3\ln x < \ln n$，那么我们这个时候就可以使用Coppersmith进行攻击，此时我们只需要构造多项式
$$
f(x)=(m_0+x)^{3}
$$
令$f(x)=0$，由于$3\ln x<\ln n$，我们可以在Sagemath中直接来f.small_roots()来解决这一问题。这也是目前最简单的一个问题了。同理，如果我把$e$上升至$5$，那么我们就需要知道八成的比特位数，满足$5\ln x < \ln n$即可。

同理，如果RSA中明文$m$满足$e\ln m <\ln n$。（$e=3$时即$3\ln m < \ln n$），那么此时我们知道了$c_1\equiv m^3 \pmod n$和$c_2\equiv (m+1)^{3} \pmod n$，那么我们可以在定义域$Z_n$中定义多项式$f(x)=x^3-c_1$和$g(x)=(x+1)^3 -c_2$，求这两个算式的公约数公约式即可。（一般是一个形如$x-a$的一次式） 这样就可以求出最终的结果了。当然，如果已知的是$(Ax+B)^3$和$(Cx+D)^3$的结果，我们也可以通过求最小公倍数的方法求出小根$x$。

1o02 低指数填充广播攻击的情况

由于已知低指数广播攻击可以使用中国剩余定理直接解决，我们设想一个这样的情形：

假设在某种情况下，为了把同一个信息发送给多人，如果我们对明文$m$进行一个较为复杂的填充$r(\mathrm{id})$，该填充式可为多项式，也可为指数式如$2^{\mathrm{id}}$，似乎这样就不会产生问题。

不过这个时候，我们还是可以通过构造多项式的方法，通过多项式求根计算来获得。

设想$m_i=x^r+i2^k$，加密指数$e$一定（比如为$3$），$i$已知。此时也可以通过构造多项式来进行低指数广播攻击

下面看一下这道题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from Crypto.Util.number import getPrime, bytes_to_long
from secret import flag
import gmpy2
import random
def pad(s,i):
    return i * pow(3,s.bit_length()) + s**2  #s.bit_length()=431
def gen_N():
    return getPrime(512) * getPrime(512)
assert len(flag) == 54
invite = bytes_to_long(flag)
e_list = [random.choice([3,5,7]) for i in range(14)]
N_list = [gen_N() for i in range(14)]
with open('./invitations','w') as f:
    for i in range(14):
        invis = pow(pad(invite,i+1),e_list[i],N_list[i])
        f.write('Invitation%d: %d \n'%(i+1,invis))
    f.write('Wait a minute! \n')
    for i in range(14):
        f.write('[e%d,N%d]: [%d,%d]\n'%(i+1,i+1,e_list[i],N_list[i]))

题目的填充$m_i=x^{2}+3^{341}i$，也是低指数广播攻击，一共给了$14$组数据。其中$e=3$四组，$e=5,7$各五组。

由于要保证$e$一定，此处选择$e=3$的$4$组数据情况。

模仿之前的中国剩余定理的步骤，我们还可以设$N=\prod_{i=1}^4 n_i$。然后设$N_i$，使$N_i$满足$N_i \equiv 0 \pmod {\dfrac{N}{n_i}}$且$N_i \equiv 1 \pmod n_i$。也就是$N_i$除以$n_i$的余数是$1$，除以$N$的其他因数的余数是$0$。

由于这里$\dfrac{\ln N}{\ln 2}=4096,\dfrac{\ln x}{\ln 2}=342$，多项式次数为$6$，满足$6\ln x<\ln n$，因此可以求出对应的根。

然后我们可以在$Z_N$中构造$f(x)=\sum_{i=1}^{4}N_i((x^2+a_i3^{341})^3-c_i)$的一个六次多项式，直接求小根即为最终答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#Sagemath 9.2
from Crypto.Util.number import *
from os import urandom
c=[
    1292****3823 ,
    814****8214 ,
    2543****4080 ,
    943****1346 
]
n=[
    1466****8391,
    650****6029,
    1261****1901,
    756****0471
]
MulNs=n[0]*n[1]*n[2]*n[3]
padd=[3,8,10,11]
for i in range(4):
    padd[i]=padd[i]*pow(3,431)
Anscrts=[0,0,0,0]
for i in range(4):
    Rem=[0,0,0,0]
    Rem[i]=1
    Anscrts[i]=crt(Rem,n)
R.<x>=PolynomialRing(Zmod(MulNs))
Gxs,Gx=[None,None,None,None],0
for i in range(4):
    Gxs[i]=Anscrts[i]*(pow(x*x+padd[i],3)-c[i])
    Gx+=Gxs[i]
Gx=Gx.monic()
Flag=Gx.small_roots(epsilon=0.035)
if(len(Flag)!=0):
    Flag.sort()
print(long_to_bytes(Flag[0]))
#b'GWHT{e959e3f8e7242954b43e1b91de9886e1}Welc0metomyp4rty'

2.简单的格构造情况

2o01 直接构造法

当然，有些时候，我们可能会组建多个未知数与已知数之间的关系，而在这其中，有极小量的出现

我们来看一下这道题：（自己出的一个Lattice入门题）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from Crypto.Util.number import *
from os import urandom
from random import randint
from secret import flag
m=bytes_to_long(flag)
p=getPrime(256)
q=getPrime(2048)
e=10007
n=p*q
f=getPrime(200)
c=pow(m,e,n)
r=getPrime(7500)
h=(p-60708760708733)*inverse(f,r)%r
ooo=open("given.py","w")
ooo.write("e="+str(e)+'\n')
ooo.write("n="+str(n)+'\n')
ooo.write("r="+str(r)+'\n')
ooo.write("h="+str(h)+'\n')
ooo.write("c="+str(c)+'\n')
ooo.close()

很显然，本题有明显的漏洞，就是$\dfrac{\ln p}{\ln 2}=256,\dfrac{\ln q}{\ln 2}=2048,\dfrac{\ln r}{\ln 2}=7500,\dfrac{\ln f}{\ln 2}=200$。已知量是$(e,n,r,h,c)$。如此巨大的差异，那就要考虑一下基本的格的关系了：

根据
$$
h\equiv (p-60708760708733)f^{-1} \pmod r
$$
我们可以得到
$$
fh\equiv p-60708760708733 \pmod r
$$
也就是
$$
fh-kr=p-60708760708733
$$
盘点一下：我们已经有了三个未知量$f,k,p$，两个已知量。为了求出有意义的未知量$f,p$，那么我们还可以增加一共式子$1f+0k\equiv f$。这样我们就构造出来$\vec xA =\vec y$的情形了。其中$A$里面均为已知量，$\vec x,\vec y$里面包含了所有的未知量。然后就可以求出$p$，分解$n$，得出最终的值了。

我们可以看到：$h,r$的比特位都是$7500$，$f$的比特位是$200$，$p$的比特位是$256$。向量$(f,-k),(1,h),(0,r)$的长度都是超过$7000$位的。而最后的向量$(f,p-60708760708733)$的向量长度仅为$300$位不到。该数值远小于$\sqrt{2 \det A}$。而每个格$L$中一定是含有一个长度小于$\sqrt n \sqrt[n]{\det L}$的向量的。$n$是格$L$的维数

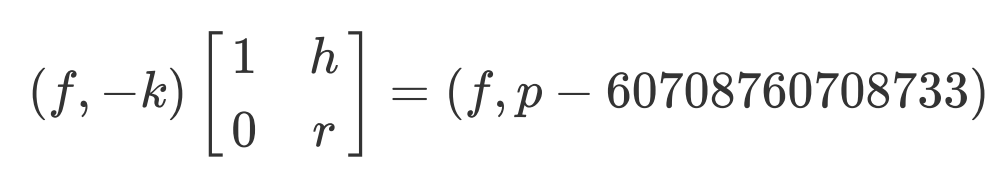
1

1
2
3
4
5
6
7
8
#Sagemath
r=3488391316101515024972590......
h=3143155356724417989594202......
M=matrix([[1,h],[0,r]])
p=M.LLL()[0][1]
p+=60708760708733
print(p,is_prime(p))
#75287619124953899281094544588134588339526984734091359573347610235691729399693 True

2o02 角最大值+对角$(1,-k)$对值构造法

有些时候，若我们知道的未知数$x_i$和已知数$a_i$的关系均为线性关系，甚至可能具有一定的同态性，并且可能出现的最大数字都不超过某个特定的值（比如$2^{128}$）之类的值。那么我们可以用此方法构造。

此类问题中最典型的一个就是我之前在LatticeNotes5中提及的一个LCG问题：假设你知道了一个$128$位的LCG的参数及其输出，但每一个LCG最后的$40$位被隐去了。让你求这个数列的完整值。

假设我们知道的所有的输出数列可表示为$u_n=a_n+x_n$。其中$a_n$是已知的高$88$位，$x_n$是未知的低$40$位。$u_{n}$和$u_{n+1}$之间的关系是$u_{n+1} \equiv Au_n+B \pmod M$。

也就是：
$$
a_{n+1}+x_{n+1} =Aa_{n}+B+x_n+k_nM
$$
建立已知数和未知数之间的关系，得：

Update 7.30 原先公式$x_n$前少了个系数$A$，已补上
$$
x_{n+1}=Aa_n+B-a_{n+1}+Ax_n+k_nM
$$
由于均为线性操作，因此我们可以设$f_2(x)=f(f(x)),f_3(x)=f(f(f(x)))$，若$f(x)=Ax+B$，则$f_2(x),f_3(x)$仍然具有线性规律。且规律为$A_{n+1}=AA_{n},B_{n+1}=AB_{n}+Aa_n+B-a_{n+1}$，不断迭代即可。

若我们已知了$6$组数据，就可以构造这样得一个格

Update 8.2： 这里原来右下角的$2^{40}$是错误的，正解是$2^{128}$

2

很显然，依然是$\vec xL=\vec y$的形式，$\vec x,\vec y$覆盖了所有的未知量$x$和$k$，$L$中所有的内容都是已知量。

而此处这个$2^{40}$就起到了一个限位的作用，该操作使得最后所有的$x$都不超过$2^{40}$，也作为了一个标志性的事物，告诉我们以$2^{40}$结尾的那一行才是答案。

我们可以再来看一下，我们构造的格是$7$维的，$M,A,B$均为$128$位，$k$也为$128$位。$\vec x$和矩阵$L$中的每一个行向量的长度均为$130$位以上。而右边的$\vec y$由于每个数字均为$40$位，因此长度约为$42$位。此处$\dfrac {\ln}{\ln 2}\det A$的值约为$680$，而短向量的长度$\dfrac {\ln}{\ln 2}|\vec y|$的值仅仅为$42$，$ \dfrac \ln {\ln 2}\sqrt 7 \sqrt[7]{\det A}>97$。因此我们所构造的短向量是符合要求的，LLL立刻出解。

还有一个典型的题目如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#Sagemath
from collections import namedtuple
PublicKey = namedtuple('PublicKey', ['n', 'b'])
SecretKey = namedtuple('SecretKey', ['p', 'q', 'A'])
def gen_key():
    p = random_prime(2^512, lbound=2^511)
    q = random_prime(2^512, lbound=2^511)
    n = p * q
    a11, a12, a21 = [random_prime(2^100) for _ in range(3)]
    a22 = random_prime(2^100)
    while a11 * a22 == a12 * a21:
        a22 = random_prime(2^100)
    A = Matrix(ZZ, [[a11, a12], [a21, a22]])
    a1 = crt([a11, a21], [p, q])
    a2 = crt([a12, a22], [p, q])
    b = a1 * inverse_mod(a2, n) % n
    PK = PublicKey(n, b)
    SK = SecretKey(p, q, A)
    return (PK, SK)
def encrypt(m, pk):
    assert 0 < m < 2^400
    r = randint(0, 2^400-1)
    c = (pk.b*m + r) % pk.n
    return c
def decrypt(c, sk):
    a2 = crt([sk.A[0,1], sk.A[1,1]], [sk.p, sk.q])
    s1 = a2 * c % sk.p
    s2 = a2 * c % sk.q
    m, r = sk.A.solve_right(vector([s1, s2]))
    return m
def test(pk, sk, num=3):
    for _ in range(num):
        m = randint(0, 2^400-1)
        c = encrypt(m, pk)
        mm = decrypt(c, sk)
        assert m == mm
if __name__ == '__main__':
    from hashlib import sha256
    from secret import m, FLAG
    assert FLAG == 'd3ctf{%s}' % sha256(int(m).to_bytes(50, 'big')).hexdigest()
    PK, SK = gen_key()
    test(PK, SK)
    c = encrypt(m, PK)
    print(f"PK = {PK}")
    print(f"c = {c}")
"""
PK = PublicKey(n=*, b=*)
c = *
"""

通过审计代码，我们可以得出一个最简单的线性内容：$r=bm-c-kn$，其中$r$是一个$400$位的随机数，而我们要求的数字就是$m$。

但我们只能得到两个式子(另一个是$1m=m$)，这个时候就可以根据$m,r$均不超过$400$位的条件，放一个$2^{400}$进行占位。然后LLL即可。

3

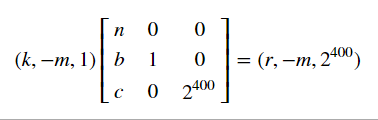
LatticeNotes5还有一个解决哈希冲突的题目，也是此类问题的典型。

这种方法就是在定上限的情况下，若我们构造的行向量$\vec x$中涉及到常数$1$，此时就可以通过$\vec x$中的那个$1$与矩阵$L$中的上限值相乘得到上限值放入结果向量$\vec y$中。

还可以点击[这里](Intended Solution to NHP in GxzyCTF 2020 | Soreat_u’s Blog (soreatu.com))对此方法身价了解。

2o03 构造大数，化大为小

根据Coppersmith定理：若多项式$f(x)$模数为$n$，次数为$e$，如果存在$x$满足$f(x)=0$且$e\ln x<\ln n$，那么符合条件的这个$x$值是可以被快速解出的。

比如看一下这道题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#Sagemath
from Crypto.Util.number import *
from os import urandom
from secret import m1,m2
def Enc(Mx,My):
    p=getPrime(400)
    a=bytes_to_long(urandom(80))%p
    b=(My**2-Mx**3-a*Mx)%p
    E=EllipticCurve(GF(p),[a,b])
    M=E(Mx,My)
    C=3*M
    return C[0],C[1],a,b,p
m1,m2=*,* #To Solve
Cipher=[]
for i in range(87):
    Cipher.append(Enc(m1,m2))
print(Cipher)

很明显，这是椭圆曲线上的低指数广播攻击，明文点$M(x,y)$，通过构造不同的椭圆曲线$E$，对这个$M$点进行了加密，但加密指数统一为$3$，也就是最后给出了在不同曲线上的$3P$值。

根据椭圆曲线上的点$x_{3P}(=c)$与$x{_P}(=x)$的关系可以得到：
$$
c=\dfrac{x^9 - 12ax^7 - 96bx^6 + 30a^2x^5 - 24abx^4 + (36a^3 + 48b^2)x^3 + 48a^2bx^2 + (a^4 + 32ab^2 + 8(a^3 + 8b^2)a)x + 8(a^3 + 8b^2)b}{9x^8 + 36ax^6 + 72bx^5 + 30a^2x^4 + 144abx^3 + (-12a^3 + 144b^2)x^2 - 24a^2bx + a^4}
$$
因此，对于题目中给出的$87$个不同曲线上的$3P$，我们都可以通过构造上面的多项式来解决这个问题，如果设上面公式中等号右边的分子部分是$S$，分母部分是$D$，那么我们可以构造$9$次多项式
$$
f_n(x)\equiv S-Dc \pmod {p_n}
$$
其中$n$从$1$取到$87$，这样就有了$87$个不同的多项式了，但这些多项式的作用域都不相同。

这个时候跟RSA中的广播攻击一样，也可以使用中国剩余定理了。但这一次的中国剩余定理的运用略有不同：首先我们计算$N=\prod_{i=1}^{87}p_i$，即所有$p$的乘积。由于$\dfrac{\ln p}{\ln 2}=400$，因此这里差不多是$\ln n=87\ln p$，$n$的比特位数迅速上涨到了$34000$以上——这比任何数都大。

然后对于所有$f_n(x)$中，从常数项到$9$次项，每一项均使用一次中国剩余定理，也就是所有常数项构成的数组对所有$p$构成的数组进行计算。并最后汇总$Z_N$上的一个非常大的九次多项式$F(x)$，该式不仅处于一个很大的环$Z_N$上，常数项到$x^8$项每一项的系数都非常大（$x^9$的系数恒定为$1$）。而我们想求的$x_P$，仍然满足$F(x_P)\equiv 0 \pmod N$。并且这里一定满足$9\ln x_P<\ln N$，可以直接用Coppersmith定理求解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#Sagemath
Cipher=[]
Cxarr,Cyarr,Aarr,Barr,Parr=[[[0] for __ in range(87)]for _ in range(5)]
for i in range(87):
    Cxarr[i],Cyarr[i],Aarr[i],Barr[i],Parr[i]=Cipher[i]
N=prod(Parr)
F=[]
for i in range(87):
    a,b,p=Aarr[i],Barr[i],Parr[i]
    R.<x>=PolynomialRing(Zmod(p))
    Fz=x^9 - 12*a*x^7 - 96*b*x^6 + 30*a^2*x^5 - 24*a*b*x^4 + (36*a^3 + 48*b^2)*x^3 + 48*a^2*b*x^2 + (a^4 + 32*a*b^2 + 8*(a^3 + 8*b^2)*a)*x + 8*(a^3 + 8*b^2)*b
    Fm=9*x^8 + 36*a*x^6 + 72*b*x^5 + 30*a^2*x^4 + 144*a*b*x^3 + (-12*a^3 + 144*b^2)*x^2 - 24*a^2*b*x + a^4
    Fx=(Fz-Cxarr[i]*Fm)
    F.append(Fx)
R.<x>=PolynomialRing(Zmod(N))
G=0
for i in range(10):
    Arrcrt=[]
    for j in range(87):
        Arrcrt.append(Integer(F[j][i]))
    G+=crt(Arrcrt,Parr)*x**i
m1=G.small_roots(epsilon=1/13)[0]
print(m1)
E=EllipticCurve(GF(Parr[0]),[Aarr[0],Barr[0]])
O=E(483680648326747026189680, 119181855961981)
(m1^3+Aarr[0]*m1+Barr[0])%Parr[0],119181855961981**2%Parr[0]
m2=min(Parr[0]-pow(14204314790542386034917444361,(Parr[0]+1)//4,Parr[0]),pow(14204314790542386034917444361,(Parr[0]+1)//4,Parr[0]))
print(m2)
print(long_to_bytes(m1)+long_to_bytes(m2))


'''
483680648326747026189680
119181855961981
flag{Example003}
'''

至于$y_{P}$怎么求，我们可以选一组带模$4$余$3$的$p$的数据，根据有限域内开平方公式，直接计算$(x^{3}+ax+b)^{(p+1)/4} \mod p$的值即可。

CTFSeason3
#Notes
Lattice Notes 7
http://example.com/2021/07/25/LatticeNotes7/
作者
huangx607087
发布于
2021年7月25日
许可协议