BlockCipher1

huangx607087学习分组密码的笔记 1

0.About

一个密码学fw的学习笔记，别看，很菜

最近这种题型在CTF中出现得越来越多，看来还是有必要关注一下的，在这里写几篇笔记。

1. DES

1o01 什么是DES

DES是一种使用$56$位密钥对$64$位长分组进行加密的密码，这也是一种对称密码，也就是其加密和解密使用相同的密钥，因此DES也是一种迭代算法。DES对铭文中每个分组的加密过程都包含16轮，且每一轮的操作完全相同，每一轮的密钥都不同，但每一轮的密钥都是由上一轮的密钥中推导出来的。

DES加密中，主要思想还是混淆与扩散：混淆是将密钥与密文之间的关系尽可能模糊——因此多数情况下的混淆就是元素替换。而扩散是为了隐藏明文的统计属性，从而将一个明文符号扩散道多个密文符号进行加密，其中最简单的一个方法就是某几位上进行置换。

下面是DES的流程图，可以看出一次DES 加密共使用了$16$次迭代，下面对图中的各部分进行分析。该图也被称为Feistel网络

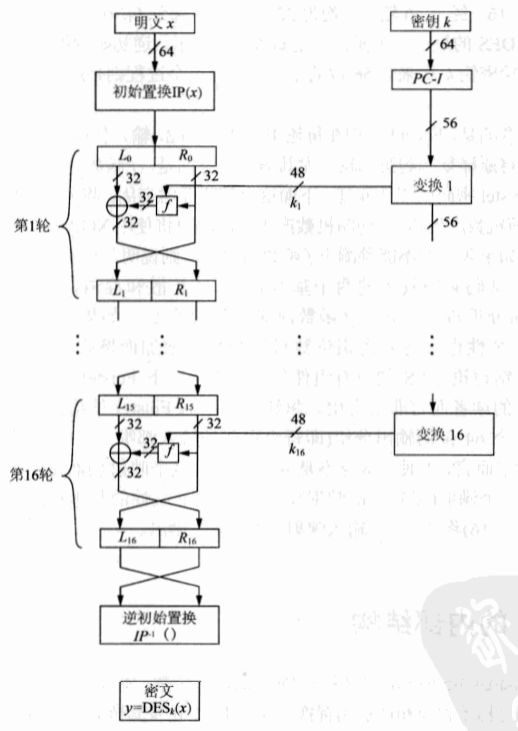
1o02 DES内部加密分析

Step 1 IP置换

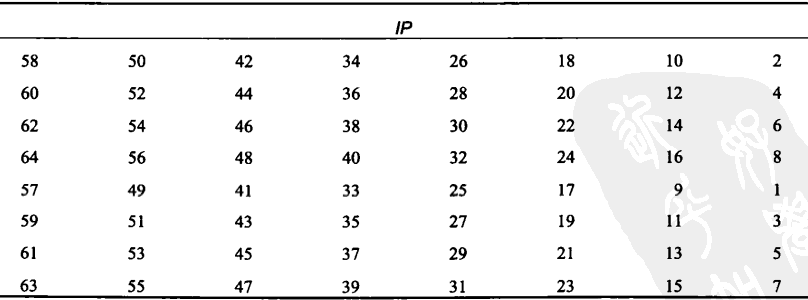
首先是对明文的一个初始置换$\mathrm{IP}(x)$进行置换，其IP置换表如下，也就是将明文$64$位的第一位变成第$58$位，第二位变成第$50$位的一个涉及比特位置换的算法。

与之对应地，由于是一对一的置换，故$\mathrm{IP}(x)$存在逆运算$\mathrm{IP}^{-1}(x)$，置换表如下图

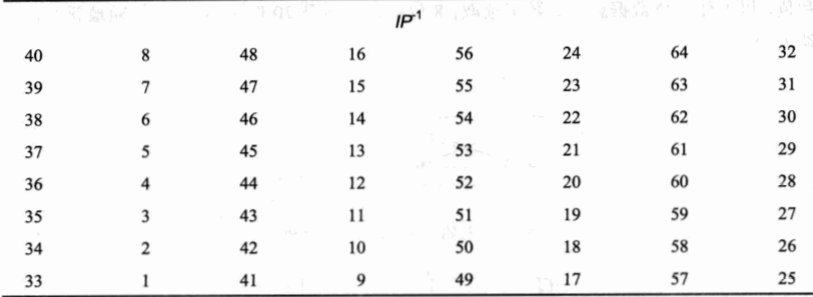
不过在这边值得注意的一点就是：与计数不同，第一位是最左边的一位，也就是计数中代表着$2^{63}$的那一位。

Step 2 $f$函数

$f$函数内部结构比较复杂，如图

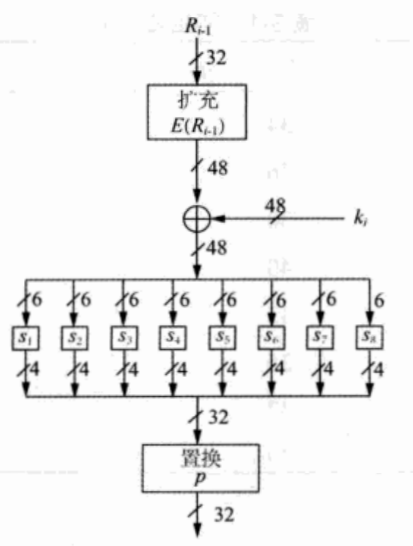
首先将右半部分$R$通过扩展$E$函数扩展到$48$位，然后与轮密钥异或后，分成$8$组，每组$6$比特，然后经过$s$盒置换后可以得到一个$32$比特位的值，经过$p$置换后获得加密后的密文。

扩展规则如下，可以看出有一半的比特位重复了$2$次——因为这样才能将$32$位内容扩展成$48$位

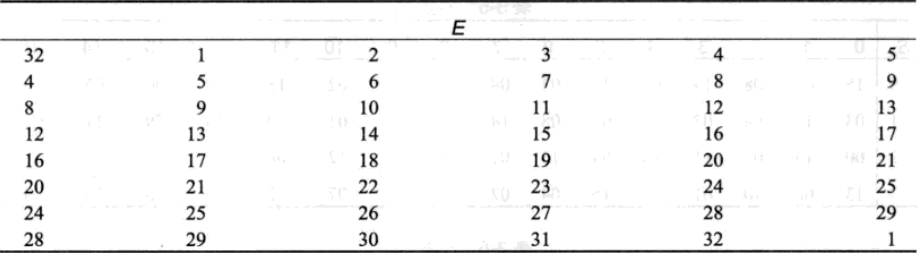
分组后，每一组都是$6$比特，$6$比特转化成$4$比特的方法也很简单：第一位和第六位组合成行数，第二位到第五位组合成列数，如$\mathrm{101100B}$拆解后就是$\mathrm{10B}$和$\mathrm{0110B}$，对应$s$盒中的第二行第六列

八个$s$盒内的内容如图所示

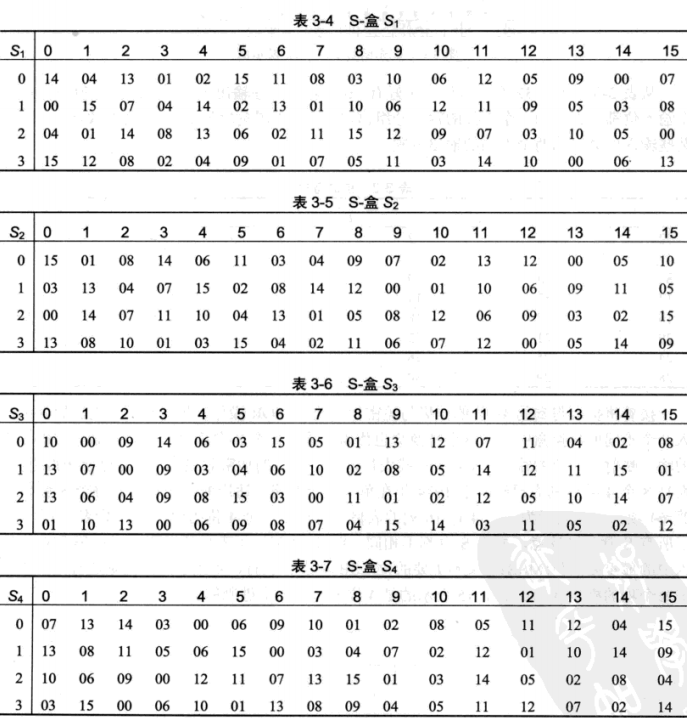
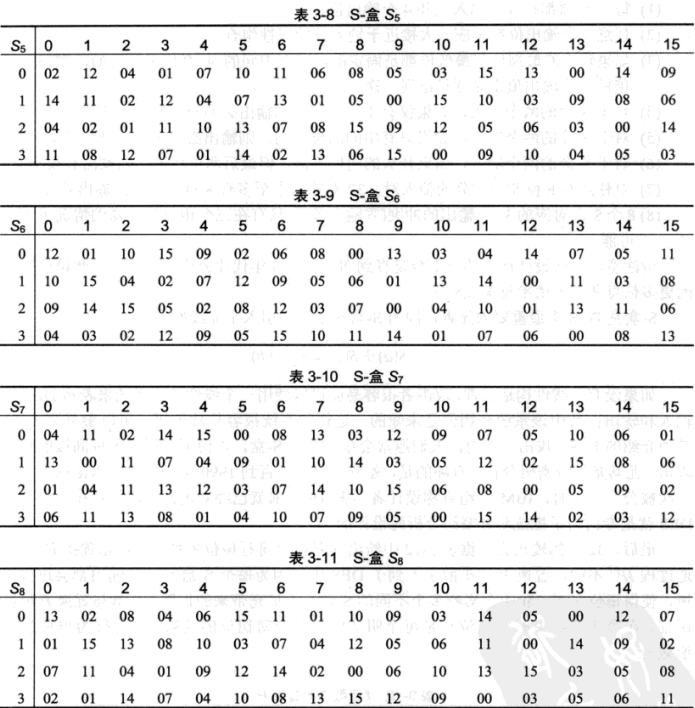
$s$盒也是DES中唯一的非线性元素，因为$s(a)+s(b)$与$s(a+b)$不同。（此处的加号表示异或）

1o03 DES密钥编排

DES的密钥编排，是先从原始的$56$位密钥中得到$16$个轮密钥$k_1,k_2,…k_{16}$，每个密钥$k_i$都是$48$位。不过在这里一个值得注意的特点就是：DES一开始的输入密钥是$64$位，八位一组，每一组的第八位是这一组的一个校验位（但这一位的意义何在不得而知）。因此实际上严格地说，DES实际上是$56$位，而不是$64$位。因为在密钥置换的时候，$64$位缩短为$56$位时，直接忽略了每一组的第八位。下表是DES初始密钥置换的表格。

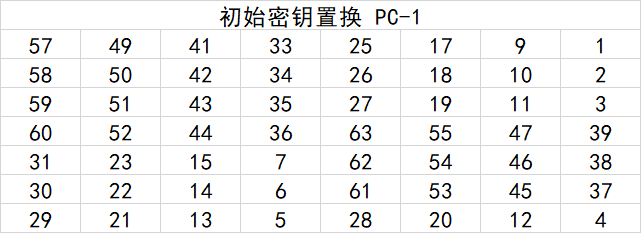
得到$56$位的密钥后，我们将密钥分为$C_0$和$D_0$两个部分，然后每一轮将每个长度为$28$位的密钥部分分别循环左移一至两位。（具体是在第$1,2,9,16$轮是循环左移一位，其他的轮都是循环左移两位。）而这样下来，我们就会发现在最后加密完成过后——$C_0=C_{16},D_0=D_{16}$。下图很清楚地表示了这一过程：

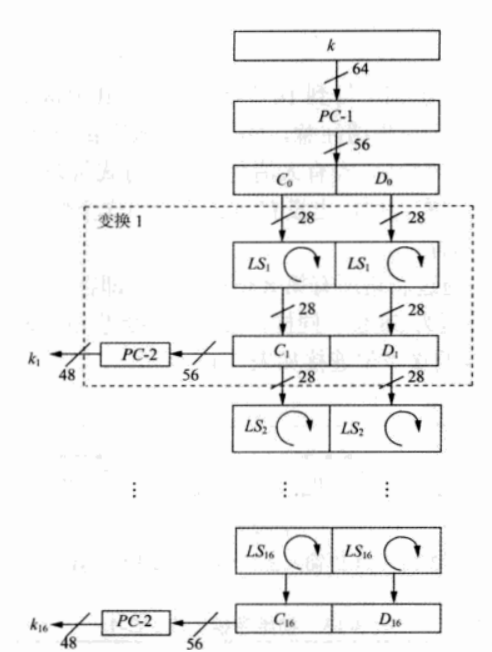
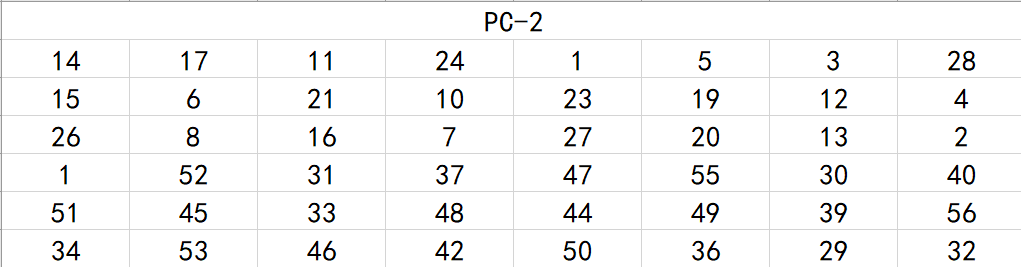
在这里，PC-2置换是将$56$位的轮密钥转化成$48$位的轮密钥，转换规则如下

1o04 DES解密过程

在解密过程中，由于我们在之前注意到$C_0=C_{16},D_0=D_{16}$的特点，因此我们可以在PC-1后直接得到$k_{16}$。

图片S1之前文字渲染有乱码问题，故使用图片修正

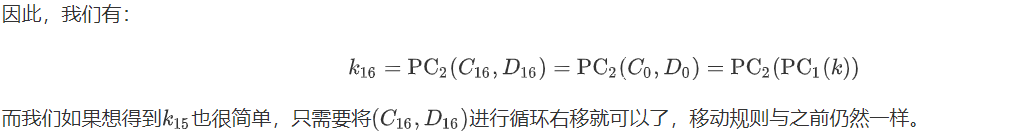
而在解密过程中，第一轮密钥不移位，第二、九、十六轮密钥移位一位，其他轮密钥移位两位。用公式可以表示为
$$
k_{15}=\mathrm{PC_2}(C_ {15},D_ {15})=\mathrm{PC_2}(\mathrm{ror}(C_ {0}),\mathrm{ror}(D_ {0}))=\mathrm{PC_2}(\mathrm{ror}(C_ {16}),\mathrm{ror}(D_ {16}))
$$
上面公式中，$\mathrm {ror,lor}$分别表示循环右移和循环左移，移动位数规则刚才已经提到过了。

整个解密过程差不多是这张图：

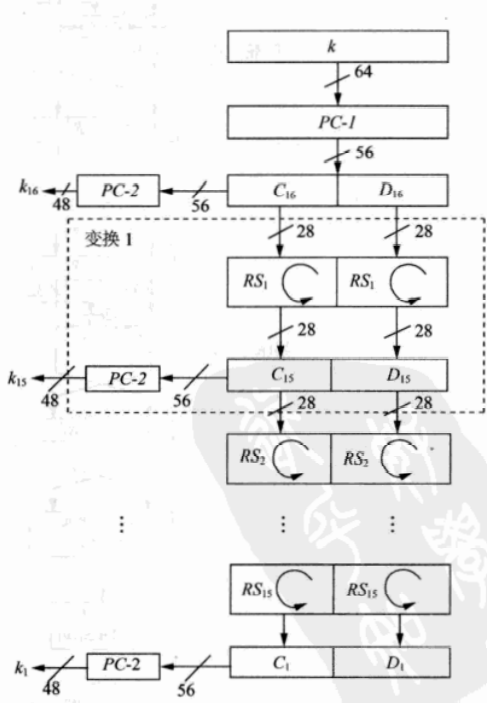
而在我们上面提到的Feistel网络中：我们需要用到IP置换的逆置换来解决问题。即
$$
(L_{D0},R_{D0})=\mathrm{IP}(\mathrm{IP}^{-1}(R_{16},L_{16}))=(R_{16},L_{16})
$$
其中下标有$D$的表示解密过程中的变量。注意到上面的Feistel网络中，有$L_{16}=R_{15}$。因此我们可以推出：
$$
(L_{D0},R_{D0})=(R_{16},L_{16})=(R_{16},R_{15})
$$
对应地，根据加密的Feistel网络，我们解密的Feistel网络密钥，很容易可以得到
$$
L_{D1}=R_{D0}=L_{16}=R_{15}
$$
不过$R_{D1}$就不是那么好算了，这里还是要用到上面提到过的刚才的$f$函数。（以下出现得加号表示异或），该计算方法可以根据异或的特性得到。
$$
R_{D1}=L_{D0}+f(R_{D0},k_{16})=R_{16}+f(L_{16},k_{16})
$$
带入$R_{16}=L_{15}+f(R_{15},k_{16})$，因此有
$$
R_{D1}=L_{15}+f(R_{15},k_{16})+f(L_{16},k_{16})
$$
又因为$R_{15}=L_{16}$，因此$f(R_{15},k_{16})+f(L_{16},k_{16})=0$。所以我们最终得到
$$
R_{D1}=L_{15}
$$
因此，即使$f$函数看似复杂，但最后得出来的结果却可以消去$f$函数。因此我们可以直接迭代，最终得到
$$
(L_{Di},R_{Di})=(R_{16-i},L_{16-i})
$$
因此这是一个非常容易的过程。

最终，我们只需要对解密后的结果计算$\mathrm{IP}^{-1}(x)$函数的处理即可获得明文。注意到一开始已经提到，由于$\mathrm{IP}(x)$是对$64$个比特位一对一的置换，因此直接对照$\mathrm{IP}^{-1}(x)$的表格置换回去即可。