BlockCipher2
huangx607087学习分组密码的笔记2
0.About
9月1日,自己的第二个90天计划开始,自己上学期的第一个90天计划很成功,自己从来没想过自己六级能考587。。。所以自己第二个90天计划主要是为了提升自己的CTF水平,争取能够打入线下,然后再恰点烂钱。。。。。(对于我这个fw还是很难的。今年三门数学一门物理,希望自己这四门课都能考到60H吧。。。
这篇博客主要是讲一下AES的算法,上承接一下DES相关内容,下启一下后面两篇笔记:笔记3: 加密模式 、笔记4: S盒差分攻击
注:若数字无后缀,默认认为是十进制。十六进制后缀会加$\text H$,例如$\text{60H}=96$
2.AES
0o01 对DES的补充内容
在正式进入AES之前,我们先对上一篇笔记中的DES进行一些补充。
由于DES的安全性在目前来看已经不是很高了,1999年1月,有一个蛮力破解DES挑战赛,有人解和Deep Track Internet 上的分布攻击,耗时22小时就破解了DES的密钥。而在2006年的4月,德国有两所大学基于低廉的FPGA,仅仅耗费了不到70000人民币的价格,构建了密钥搜索机器,平均搜索时间仅仅7天。
因此,出现了一些DES的替换算法,其中最典型的就是3DES,有的3DES使用三个不同的密钥,对明文连续加密三次。当然也有使用两个密钥的3DES,使用函数如下
$$
c=E_1(D_2(E_1(m)))
$$
也就是先用密钥$k_1$对明文进行加密,然后用密钥$k_2$对加密后内容进行解密,最后再用密钥$k_1$对内容进行加密,输出最终的密文。
当然,这种加密方法也仅仅是在DES上加了个变体,解密函数也是三次
$$
m=D_1(E_2(D_1(c)))
$$
但这边有个问题就是3DES耗时增加至原来的$3$倍,比较影响效率
DES加密算法有几个弱密钥,这些密钥有个特点,就是在分组后,会使得$C$和$D$无论怎么左移,均为全$0$或者全$1$的128位序列。
DES的弱密钥在不考虑第八位校验位的情况下,一共有八个弱密钥:
1 | |
如果用这$8$个弱密钥加密明文$m$,会出现一个很好玩的现象:
$$
m=E(c)=E(E(m))
$$
也就是说,对明文两次加密,就可以得到原来的明文。
0o02 AES简介:
AES与DES一样,也是一种对称分组密码。其分组大小比DES要大,有$128,192,256$位三种长度的密钥,但AES中每个分组一般均为$128$位,其主要操作简图如下:
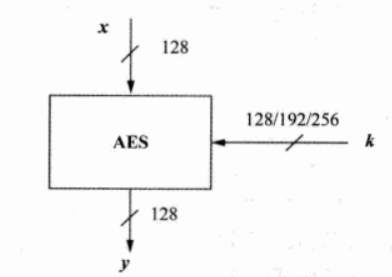
而加密轮数一般也有固定规则——在$128$位密钥下加密$10$次,$192$位密钥下加密$12$次,$256$位密钥下加密$14$次。而加密轮数较少的一个主要原因就是AES与DES不一样,每次直接对所有的$128$位进行了处理。
AES的总体加密框图如下:
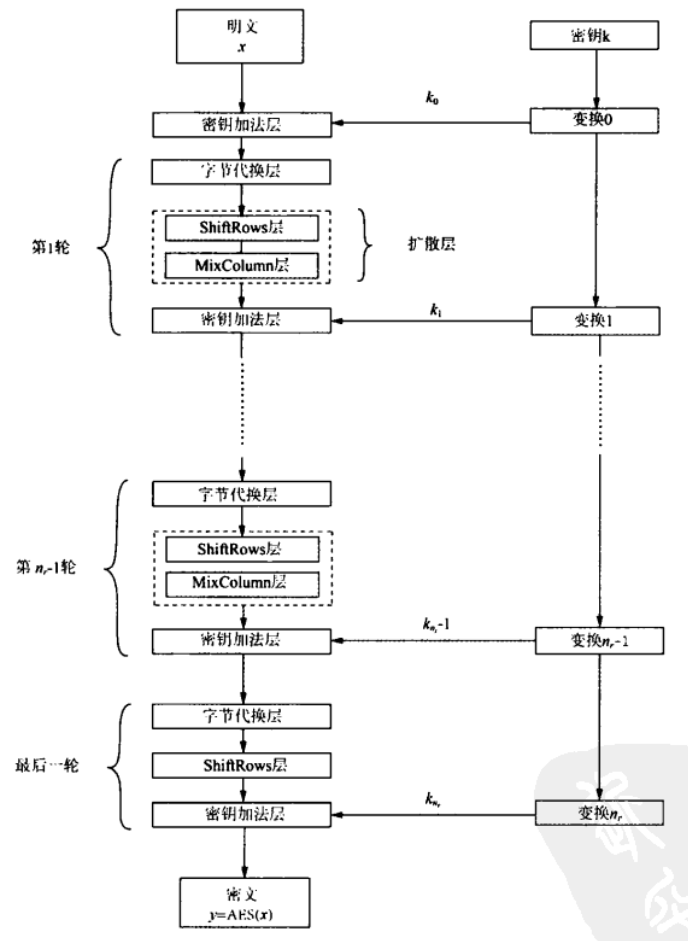
AES中,对于每一轮加密有三层,第一层是字节代换层,在这里使用$S$盒,对每个字节元素(8bit)根据$S$盒的变换规则进行非线性变换。
第二层是扩散层,由ShiftRows和MixColumn。其中ShiftRows是对行的位移变化,在位级别进行数据置换。而MixColumn是对列的混淆变换,合并长度为四个字节(32bit)的数据。
第三层是密钥加法层,这里主要是通过$128$位的轮密钥,与状态进行异或操作的过程。
在AES中,我们还会涉及到在$GF(256)$中的操作,这里用的是不可约多项式$x^8+x^4+x^3+x+1$。$GF(256)$下对于该多项式有如下的逆元表(为方便期间与避免争议,特别规定$0$的逆元为$0$)。
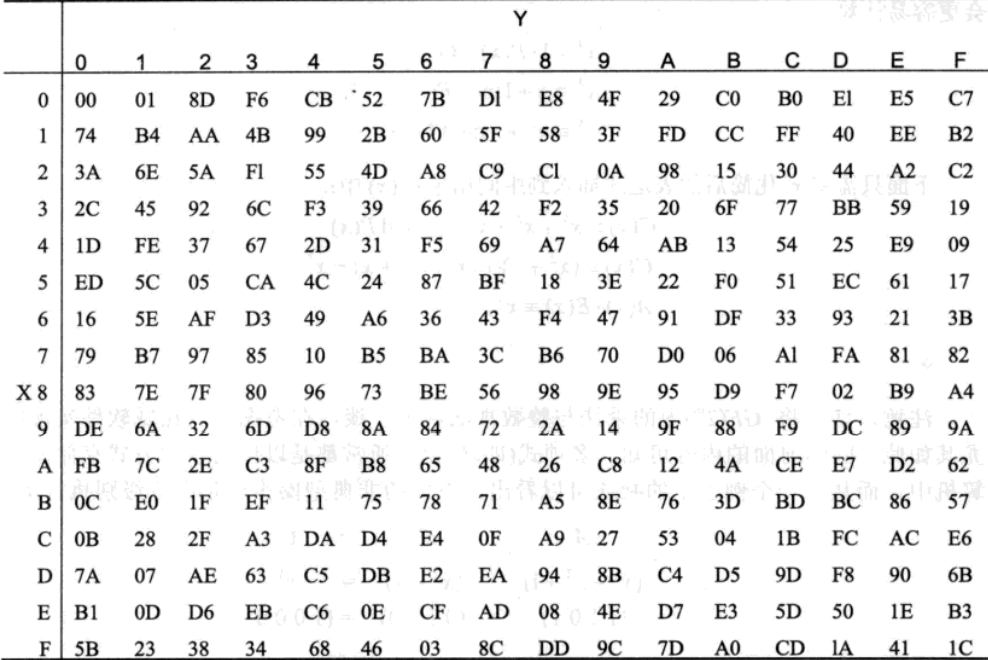
举个例子:上表中$\mathrm{00H}$表示$0$,$\mathrm{C2H}$表示二进制的$\text{1100 0010B}$,对应多项式就是$x^7+x^6+x$,它的逆元为$\mathrm{25H}$,其表示多项式为$x^5+x^3+x^2+1$,这两个式子相乘,并对$x^8+x^4+x^3+x+1$取模,结果恰好是$1$。
0o03 AES加密过程
Step 1 AES内部结构
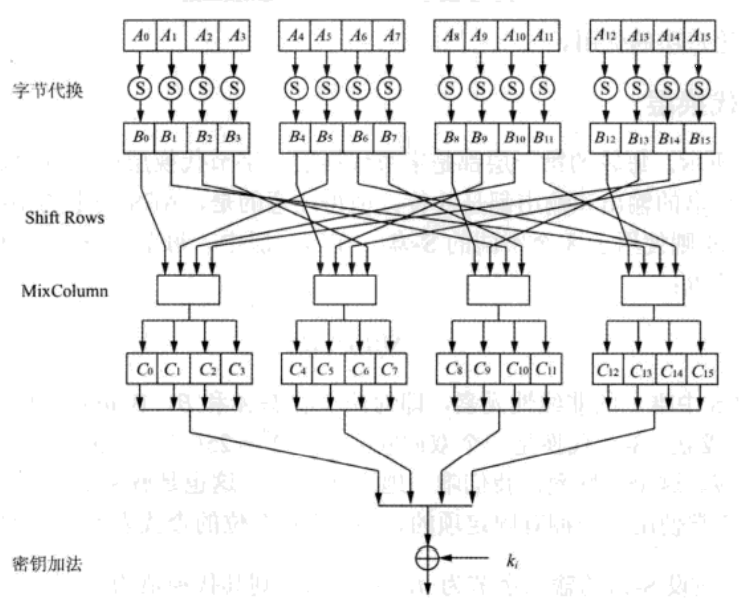
Step 2字节代换层
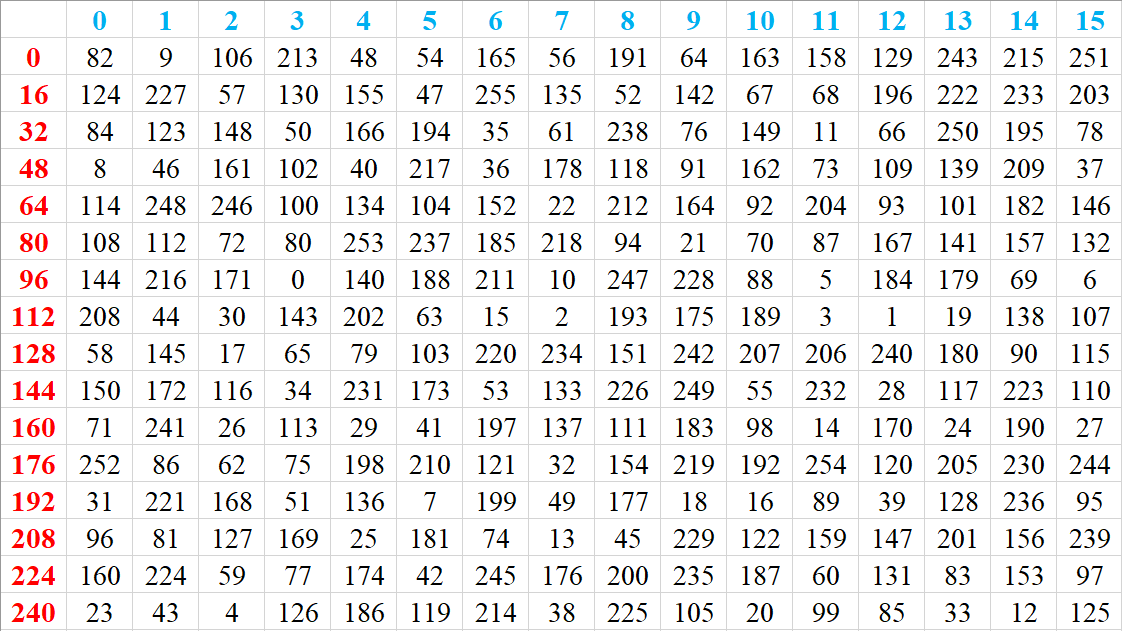
由于$128$位对应十六个字节,因此字节代换中,有特定的$S$盒。其数值如下(十进制):
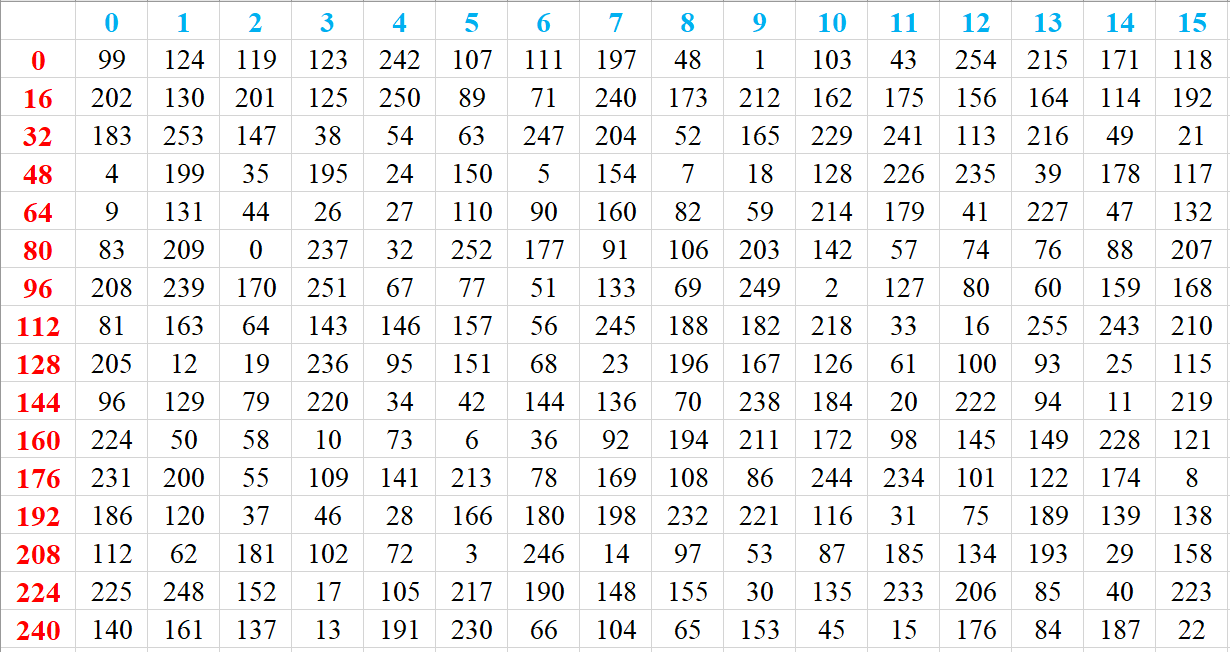
这个$S$盒有个特点就是:不存在$x\in [0,255]$使得$S(x)=x$。
因此,即使我们输入的内容是$(0,0,0,…,0)$,到一次$S$盒最后也会输出十进制$(99,99,99,…,99)$,然后再经过$S$盒变成十进制$(251,251,251,…,251)$。因此,AES与DES不同,它不存在弱密钥。
Step 3 扩散层和密钥加法层
在扩散层中,对十六个$B$,进行了如下的操作:
首先是位置替换,下标值按照$(0,5,10,15,4,9,14,3,8,13,2,7,12,1,6,11)$的规则重新排列成新的顺序。
然后是列置换,$B_0,B_5,B_{10},B_{15}$通过下面的操作,获得了$C_0$到$C_4$

这边说一下,这里的$01,02,03$代表着$(1,x,x+1)$,整个式子的计算是基于$GF(256)$的多项式运算,也就是说如果$B_0=99$,那么就是转化成$x^6+x^5+x+1$,然后最后还是对$x^8+x^4+x^3+x+1$取模即可。计算出来的多项式再转化成数字即可得到$C_0$到$C_3$的值。
当然,我们还可以通过$B_4,B_9,B_{14},B_3$,用组合成列向量,然后用相同的矩阵得到$C_4$到$C_7$的值,以此类推。
最后对得到的十六个$C$值(每个数八位,因此一共是$128$位)组合在一起,对密钥异或即可。完成一轮的加密。
0o04 密钥编排
下面我们以$128$位密钥编排为例,$192,256$位密钥编排只需要把一行四组换成六组、八组即可,总轮数换成十二轮和十四轮即可。
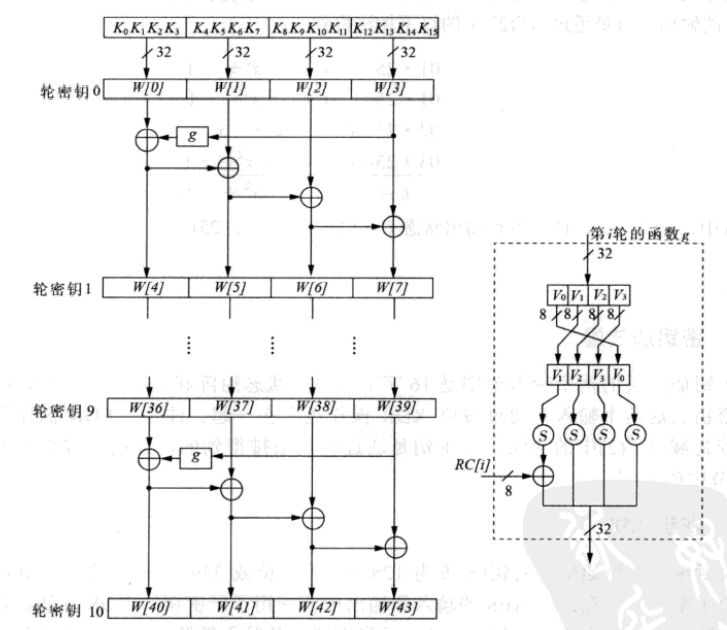
这边$RC[i]$也提一下,实际上就是$x$的$i$次方,这里分别需要用到$0,x^1,x^2,…,x^9$,模多项式为$x^8+x^4+x^3+x+1$。因此$x^8\equiv x^4+x^3+x+1$,$x^9\equiv x^5+x^4+x^2+x$。这边这个$g$函数的目的也是增加密钥编排的非线性内容。
0o05 解密过程
作为对称密码,解密过程与与加密过程差不多是一致的。
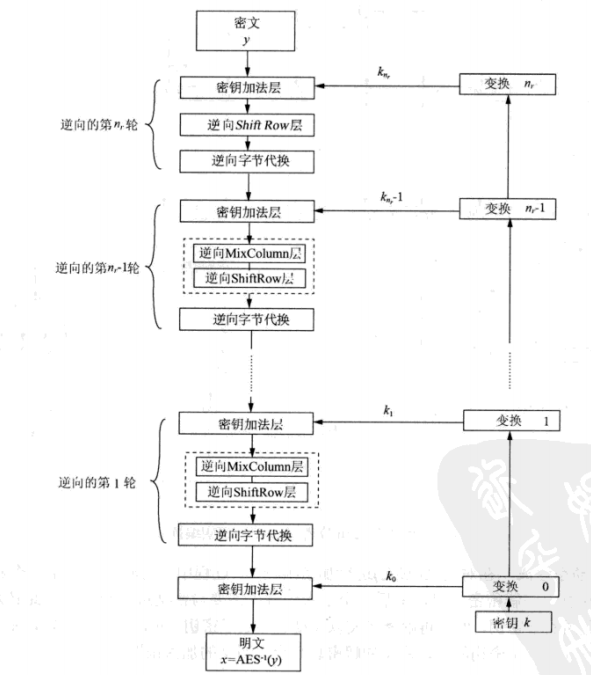
所以,我们只需要将我们加密中所做的内容逆回去即可。
下面是解密过程
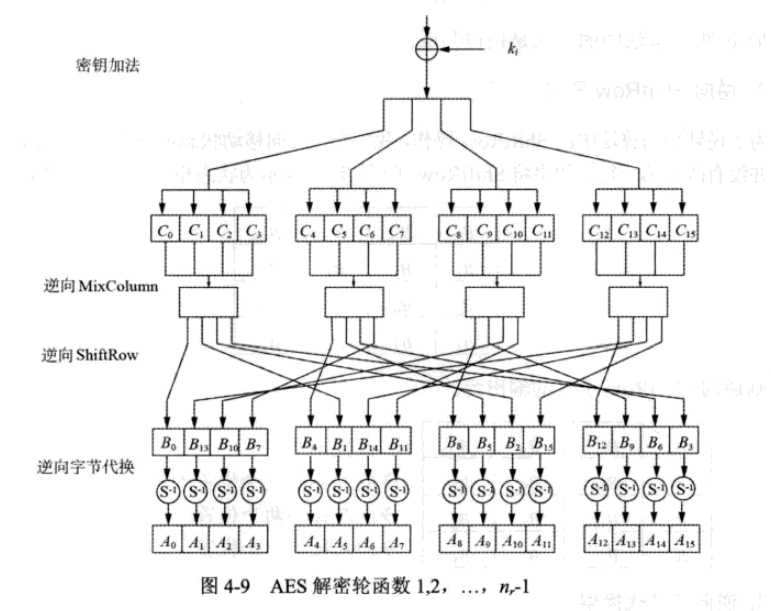
因此密钥加法还是轮密钥与密文异或,逆向MixColumn与逆向ShiftRow也是一个可逆过程,直接乘上逆矩阵,做逆变换即可。
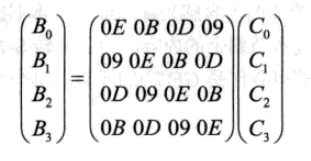
逆矩阵的内容如下,这边的$0EH,0BH,0DH,09H$仍然是$GF(256)$中的多项式,可以逆回$B$。
然后根据变换$(0,13,10,7,4,1,14,11,8,5,2,15,12,9,6,3)$的变换规则,得到所有逆向shiftrow后的$B$值,最后根据逆向后的所有$B$值获取$A$值。
那么我们也可以获得$S^{-1}$