BlockCipher3

huangx607087学习分组密码的笔记3

0.About

一个密码学fw的学习笔记，很菜。

最近自己不知为何总想着摸鱼，算了，还是要以学习为重。

本篇博客接着前一篇的内容，在讲过DES AES后，对其加密模式进行分析。

3.DES,AES的加密模式

在DES 和AES的各种加密模式中， 有五种操作模式最为常用，下面将逐一介绍下面的各种加密模式。

0o01 电子密码本模式 ECB

ECB模式是最简单的一种模式，实际上就是直接加密和直接解密，不需要其他的任何成分，仅需要明文$x$和密钥$k$，就可以获得密文$y$，当然，用$y$和$k$也可以通过解密得到$x$。

在ECB模式中，每个分组的长度都是固定的，比如$16$个字节或者$8$个字节。如果最后不满$16$个字节，那就需要对最后一组明文进行填充后加密。一种常见的填充模式就是后面差几个，就往后面填几个对应字符。例如：在$8$字节的分组下，对字符串doge进行加密，由于差$4$个才能满足一组八个的要求，那就在后面填充四个\x04再加密，也就是最后明文变成了doge\x04\x04\x04\x04。当然，如果刚好是八个字节了，那就填充一整串。例如：nuptsacc在填充后，从一组变成了两组，内容是：nuptsacc\x08\x08\x08\x08\x08\x08\x08\x08

ECB模式的优点就是如果在加密时，某个分组的内容出现了错误，后面的内容不会因为这个错误而受到影响，并且加密速度快、效率高、易操作。

但ECB模式的缺点也很明显，就是该模式由于操作过于简单，具有高度确定性。如果在key一定的情况下，那么一旦$x$确定了，$y$也就确定了。因此如果攻击者知道了文件开头部分，或者是是文件的高频内容，就有可能破解出可能的密钥。

由于内容的高度确定性，因此ECB在对于图片加密的情况下，有可能会泄露信息，如下图:

0o02 密码分组链接模式(CBC)

CBC模式跟ECB模式不同：首先，对于某一组的加密不仅依赖于这一组的内容，还依赖于前面所有的明文分组。并且会使用初始向量IV对加密进行随机化。设$\mathrm {IV}=y_0$，那么我们有
$$
y_i=e(x_i+y_{i-1})
$$
此处的加号仍然表示异或，你会发现每一组的加密内容是把这一组的明文和上一组的密文异或之后，再启用加密算法进行加密。加密算法可以用这张图表示

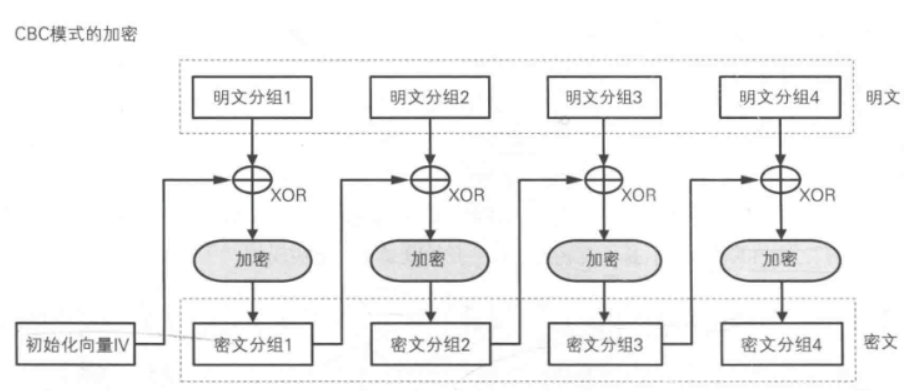
因此，这个加密有个性质：就是由于$y_i=E_k(x_i,y_{i-1})$，我们可以得到$x_i=D_k(y_i,y_{i-1})$，由于异或的可交换性，我们也可以得到
$$
y_{i-1}=D_k(y_i,x_{i})
$$
也就是凭借一组明文$x$和一组密文$y$，当然还有密钥$k$，我们可以求出$iv$的值。

首先我们可以给服务器发送一个fakeiv $f$，计算：
$$
x’=D_k(y,f)
$$
那么我们可以得到：（加号表示异或）
$$
y’=x’+f
$$
然后我们可以得到真正的IV，也就是$y_0$的值为
$$
y_0=y’+x
$$

整合起来，那就在已知明文$x$、密文$y$、密钥$k$的情况下，初始向量$y_0$很快就能直接求出（加号表示异或）
$$
y_0=D_k(y,f)+f+x
$$

0o03 输出反馈模式(OFB)

OFB模式是对初始化向量$iv$进行加密，然后每次对加密后的$iv$直接异或明文$x$，从而获得密文$y$的一种模式。

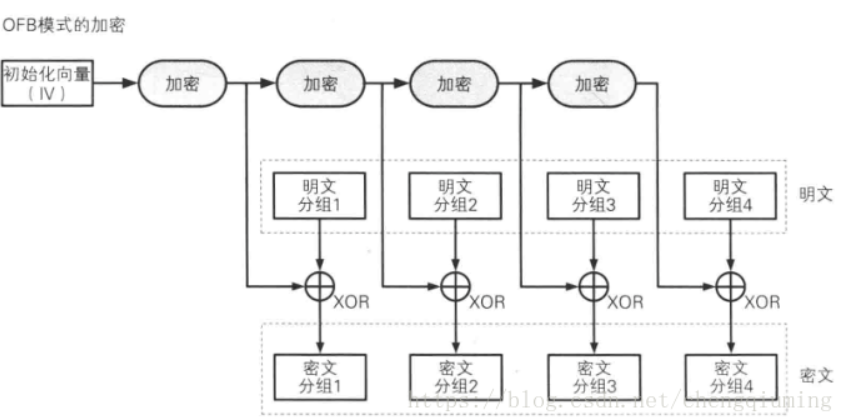
因此，我们解密时，也直接使用IV进行解密即可，不过注意对于IV来收，仍然是加密操作，而不是解密操作。换句话说就是对于IV而言，不存在解密操作。

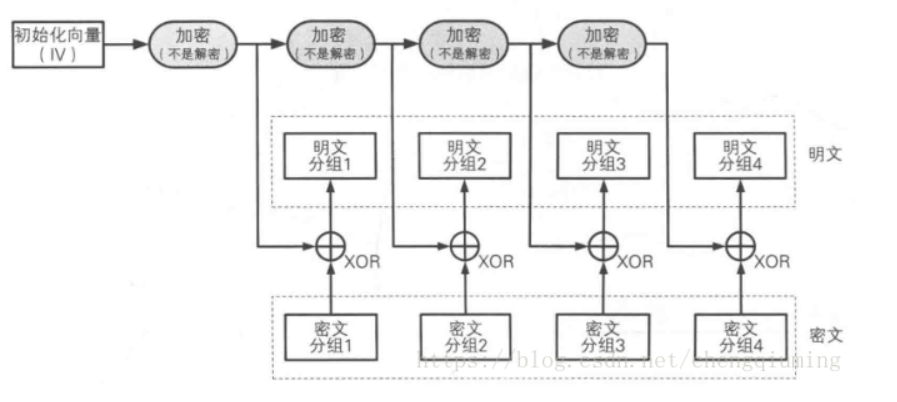
0o04 密码反馈模式(CFB)

CFB，即密文反馈模式，仍然是对IV进行加密，然后与明文$x$进行异或得到密文$y$。然后$E(IV)$会继承后半部分内容作为新的前半部分，而新的后半部分则由密文的后半部分组成。如果是$16$位，替换$8$位。那么就是新的IV的前$8$位是旧的IV的后$8$位，然后新的IV的后$8$位是密文的后$8$位（当然也可以是前$8$位）

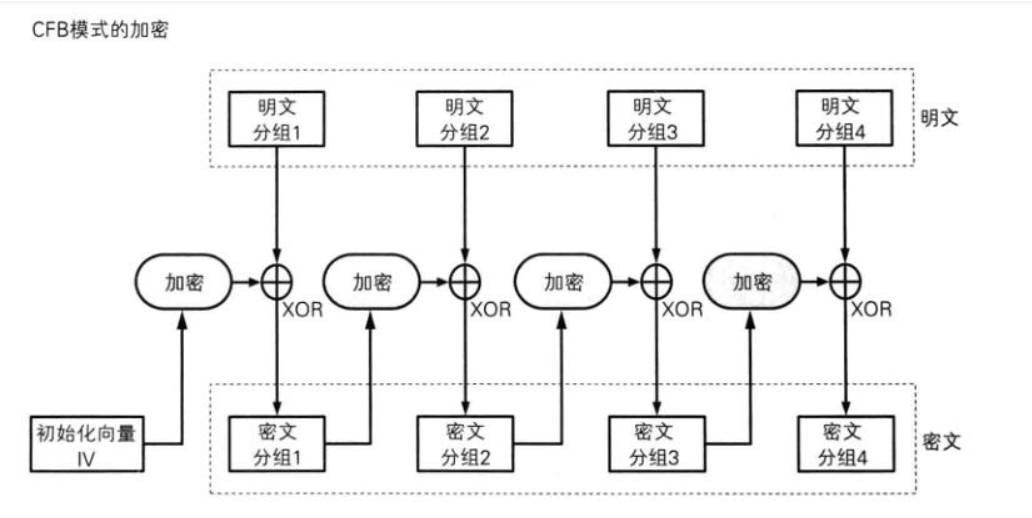
解密时，也直接就是分组解密，对IV加密后与密文异或得到明文。与OFB模式一样，不存在对IV解密的情形。

0o05 计数器模式(CTR)

CTR模式这里有一个计数器。比如在$64$位的分组加密中，IV只提供$48$位，剩下的$16$位分配给计数器。例如：如果我们设$\text{IV = 86 43 23 6A 46 57H}$，那么一开始的$\text{IV=86 43 23 6A 46 57 00 00H}$，第二轮加密时用$\text{IV=86 43 23 6A 46 57 00 01H}$。每一次加密时，计数器会保持递增，但IV会一直不变。因此，十六位的计数器可以加密六万多组数据。

当然，IV|CTR的值实际上不必保密，而CTR也并不一定是+1形，可以是最大长度LFSR，也可以是离散对数的规律，比如$ 3^{T} \equiv \mathrm{CTR} \pmod {2^{64}}$。

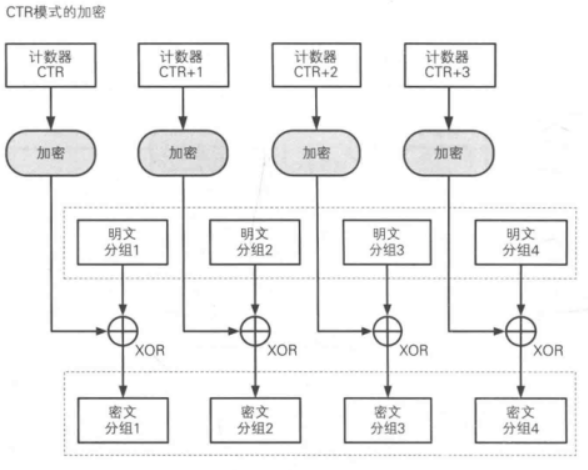
这种模式还有个好处，我们可以通过128位的内容来加密$256$位的分组密码。我们只需要每次让计数器$+2$，一组加密前$128$位，一组加密后$128$位。两组加密同时进行，可以节省较多的时间成本。

0o06 GF域计数器模式(GCM)

GCM模式，使用伽罗瓦域乘法，这里是$GF(2^{128})$。在计算每个明文时都会得到一个中间认证参数$g$，$g_{i}$为当前密文$y_i$异或后，与一个常数$h$相乘。这里使用不可约多项式$x^{128}+x^7+x^2+x+1$。因为这里面只有一个乘法，因此GCM的计算开销不会很大。

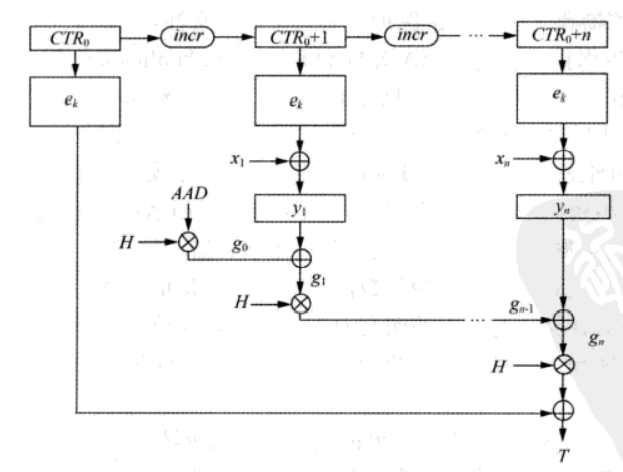
数据包$[y,T,ADD]$的接收者也是使用计数器模式解密密文。为了检査数据的可靠性，接收者也使用收到的密文$ADD$与 $T’$ —起计算认证标签 r,而且接收者的计算步骤 与发送者完全相同。如果 $T$与$T’$ 匹配，接收者则可确定密文(和 在传输过程中没有被 篡改，并且的确是发送者生成了该消息。

了解这些加密模式 的原理图，对我们以后在做到分组密码的题目时，可以从原理出发，更加深入地对其算法进行研究。