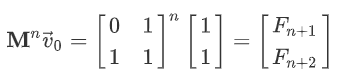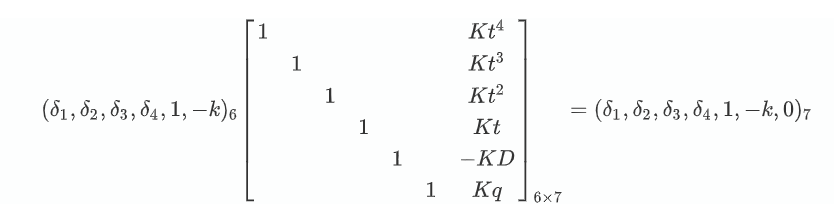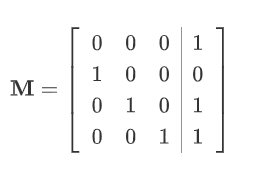SUSCTF2024

huangx607087-SUSCTF WriteUp

Crypto 9 题做了 7 题，两年没碰CTF，好多都不会了，手感全损。。。

1.RSA教学

一开始看到还以为是pad部分是三L，然后一个Easy题一天多0解，没想到竟然是个错题。更新的时候刚好本科几个舍友找我玩，抢血失败

打开容器，连接17次，获取17组 $n$ 和 $c$，然后直接CRT即可。

用sagemath可以一把梭，代码过于简单

1
2
3
4
5
6
7
8
from gmpy2 import iroot
from Crypto.Util.number improt *
N=[...] #得到的17个n
C=[...] #得到的17个c
m17=crt(C,N)
msg,judg=iroot(m17,17)
assert judg
print(long_to_bytes(msg))

2.pell

签到题，解方程 $x^2-114514y^2=1$，很简单的pell方程

直接从网上down一个代码，OK。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import numpy as np
from collections import deque

d =114514
m = int(np.sqrt(d))
dq = deque()
dq.append(m)
n0 = n1 = d - m * m
m1 = m
while 1:
    q, m2 = divmod(m1 + m, n1)
    dq.appendleft(q)
    m1 = -m2+m
    n1 = (d-m1*m1)//n1
    if m1 == m and n1 == n0:
        break

dq.popleft()
x = 1
y = 0
for i in dq:
    x1 = y + x * i
    y = x
    x = x1
    y1=y
if x*x-d*y*y==-1:
   b=(x**2+d*y**2)
   y1=2*x*y
   x1=b
print('x1=',x1)
print('y1=',y1)

3.fermat

题目给出了 $n=pq$ 和 $g=p^3+q^3$，设 $P=p^3,Q=q^3$，有 $n^3=PQ,g=P+Q$。
构造二次方程 $x^2-gx+n$，使用求根公式可以得到 $x_1=P,x_2=Q$，再对 $P,Q$ 开立方，得到 $p$ 和 $q$。
由于 $p,q$ 均为模 $4$ 余 $1$ 的素数，因此它们均可表示为两个平方和的形式，设 $p=a^2+b^2,q=u^2+v^2$。
可以得到
$$
n=pq=(a^2+b^2)(u^2+v^2)=(ua+vb)^2+(va-ub)^2
$$
用递降法求出 $a,b,u,v$ 即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
from pwn import *
from hashlib import sha256
from Crypto.Util.number import *
from os import urandom
from gmpy2 import iroot


def getyanzhengma(s16len, s64len):
    LTSNMS = "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789"
    assert len(s16len) == 12 and len(s64len) == 64
    for i1 in LTSNMS:
        for i2 in LTSNMS:
            for i3 in LTSNMS:
                for i4 in LTSNMS:
                    if sha256((i1+i2+i3+i4+s16len).encode()).hexdigest() == s64len:
                        return i1+i2+i3+i4


def getA(p):
    assert(p % 4 == 1)
    while 1:
        t = bytes_to_long(urandom(195)) % p
        s = pow(t, (p-1)//4, p)
        if(pow(s, 2, p) == p-1):
            return s


def getAns(A, B, M, p):
    # print(A,B,M,p)
    if(M == 1):
        return (abs(A), abs(B))
    # print(A,B,M,p)
    u, v = A % M, B % M
    if(u > M//2):
        u -= M
    if(v > M//2):
        v -= M
    assert((u**2+v**2) % M == 0 and (A**2+B**2) % M == 0)
    r = (u**2+v**2)//M
    A2 = (u*A+v*B)//M
    B2 = (-u*B+v*A)//M
    return getAns(A2, B2, r, p)


def solve(p):
    A = getA(p)
    B = 1
    assert(A**2+B**2) % p == 0
    M = (A**2+B**2)//p
    return getAns(A, B, M, p)


sh = remote('game.ctf.seusus.com', 57718)
cc = sh.recvline(keepends=False)
s64 = cc[-64:].decode()
s16 = cc[12:24].decode()
print(cc)
print(s64)
print(s16)
yanzhengma = getyanzhengma(s16, s64)
print(yanzhengma)
sh.recvuntil(b':')
sh.sendline(yanzhengma.encode())
sh.recvuntil(b'=')
n = sh.recvline(keepends=False)
sh.recvuntil(b'=')
g = sh.recvline(keepends=False)
print(n)
print(g)
n, g = int(n), int(g)
PmulQ = n**3
PaddQ = g
A, B, C = 1, -PaddQ, PmulQ
sqrtdet, judg = iroot(B**2-4*A*C, 2)
print('J:', judg)
P = (-B+sqrtdet) >> 1
Q = (-B-sqrtdet) >> 1
p, q = iroot(P, 3)[0], iroot(Q, 3)[0]
print(p, q, n % p, n % q)
u, v = (solve(p))
a, b = (solve(q))


Ans = abs(u*a+v*b)
Bns = abs(v*a-u*b)
print(Ans)
print(Bns)
print(Ans**2+Bns**2 == n)
sh.recvuntil(b'=')
sh.sendline(str(Ans).encode())

sh.recvuntil(b'=')
sh.sendline(str(Bns).encode())
sh.interactive()

4.Fibonacii

题目给出了一个已知值 $A=\mathtt{target}$，要求给出 $p$ 和 $n$，使得 $F_{n}\equiv A \pmod p$。

注意到斐波那契数列的矩阵快速幂形式（令 $F_0=0,F_1=F_2=1$）：

4-1

其中矩阵 $\mathbf M$ 有特征值 $t_1=\dfrac{1+\sqrt 5}{2}$ 和 $t_2=\dfrac{1-\sqrt 5}{2}$，其对应的特征向量分别为 $\vec v_1=(1,\dfrac{1+\sqrt5}{2})$ 和 $\vec v_2=(1,\dfrac{1-\sqrt5}{2})$。
再注意到斐波那契数列的通项公式 $F_n = \dfrac{1}{\sqrt{5}} \left[ \left( \dfrac{1 + \sqrt{5}}{2} \right)^n - \left( \dfrac{1 - \sqrt{5}}{2} \right)^n \right]$。很明显，这个题有 $\sqrt5$、$n$ 次方两个要素。那就要从离散对数、二次剩余的地方去想。

根据信安数基的知识可以知道：

  1. 若 $5$ 是 $p$ 的二次剩余，则 $p\equiv ±1\pmod5$
  2. 若 $p-1$ 极度光滑，则离散对数极度易解。

因此，构造 $p=754×10^{74}+1$ ，显然 $p-1$ 极度光滑，且 $p\equiv 1\pmod 5$。然后用下面的代码求出 $x \equiv \sqrt 5 \pmod p$ 的值。这个代码主要是用来求模 8 余 1 的素数域开平方的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
# luogu P5491
# P.S. 自己高中搞过OI(省2)，luogu其实带着刷过一些算法题，主要还是偏模板和数据结构一点，接触CTF后为了熟悉和验证算法也做过难一点的数论。本科没打过ACM，ACM肯定不行的。
from Crypto.Util.number import *
from os import urandom
class Complex:
    def __init__(self,x=0,y=0):
        self.real=x
        self.imag=y
def isqr(x,p): #勒让德符号
    if p==1 or x==1:
        return 1
    sgn=1
    while x&1==0:
        x>>=1
        if p&7==3 or p&7==5:
            sgn=-sgn
    if x<p:
        x,p=p,x
        if x&3==3 and p&3==3 :
            sgn=-sgn
    return sgn*isqr(x%p,p)
def Rand(p): #随机数
    return bytes_to_long(urandom(80))%p
def Cmul(a,b,nr,p): #复数乘
    Real=a.real*b.real+a.imag*b.imag*nr
    Imag=a.real*b.imag+b.real*a.imag
    Res=Complex(Real%p,Imag%p)
    return Res
def Cpow(a,e,nr,p):
    Res=Complex(1)
    while e:
        if e&1:
            Res=Cmul(a,Res,nr,p)
        a=Cmul(a,a,nr,p)
        e>>=1
    return Res
def solve_M8R1(n,p): #模8余1开平方
    while 1:
        a=Rand(p)
        nr=(a*a-n)%p
        if isqr(nr,p)==-1:
            break
    Res=Complex(a,1)
    return Cpow(Res,(p+1)//2,nr,p)
def solve(n,p): 
    A=None
    if n==0:
        return str(0)
    if isqr(n,p)==-1:
        return "Hola!"
    if p&3==3: #有公式的套公式
        A=pow(n,(p+1)//4,p)
    elif p&7==5:
        A=pow(n,(p+3)//8,p)
        if pow(A,2,p)!=n:
            A=2*n*pow(4*n,(p-5)//8,p)%p
    elif p&7==1: #没公式的就那么做
        A=solve_M8R1(n,p).real
    return str(min(A,p-A))+" "+str(max(A,p-A))
T=int(input()) 
while T: #OI特有的code style
    T=T-1
    n,p=input().split()
    print(solve(int(n),int(p)))

然后一些带 $\sqrt 5$ 的值就解出来了：

1
2
3
4
5
6
7
8
9
10
11
12
from Crypto.Util.number import *
p=75400000000000000000000000000000000000000000000000000000000000000000000000001 
#very weak prime,p-1=2^75 * 5^74 * 13 * 29
sq5=16392361170112101659662823978726961447340641722259199851531537362443024593275
half=pow(2,p-2,p)
t1,t2=half*(1+sq5)%p,half*(1-sq5)%p
"""
half=37700000000000000000000000000000000000000000000000000000000000000000000000001
t1=8196180585056050829831411989363480723670320861129599925765768681221512296638
t2=67203819414943949170168588010636519276329679138870400074234231318778487703364
"""

根据特征值的概念，可以得到：
$$
\mathbf M^n v_0=t_1^n k_1\vec v_1+t_2^nk_2\vec v_2
$$
其中 $\vec v_0=(1,1)$，可以写成 $\vec v_0=k_1\vec v_1+k_2\vec v_2$ 的形式，$k_1,k_2$ 直接列二元一次方程解出

1
2
3
4
5
6
7
8
9
10
11
k1=(1-t2)*inverse(Integer(t1-t2),p)%p
k2=(1-k1)%p
print(k1)
print(k2)
v1=vector([1,t1])
v2=vector([1,t2])
print(k1*t1**1+k2*t2**1)
"""
k1=1639236117011210165966282397872696144734064172225919985153153736244302459328 k2=73760763882988789834033717602127303855265935827774080014846846263755697540674
check=1
"""

注意到两个特征值之间的关系： $t_1t_2=-1$，因此设 $t_2=\dfrac{-1}{t_1}$。由于 $A$ 是第 $x$ 项，因此有：
$$
k_1t_1^x+k_2t_2^x=A
$$
令 $t_1^x=t$，消元去分母可以得到
$$
k_1t^2-At-k_2=0
$$
放到sagemath中分解这个式子，可以得到

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#t1*t2=1
# let t1=g t2=-1/g
# k1*g^x-k2/g^x=A
# let g^x=t
# k1*t-k2/t=A
# k1*t^2-A*t-k2=0
var("t")
TRR.<t>=PolynomialRing(GF(p))
factor(k1*t**2-A*t-k2)
"""
(1639236117011210165966282397872696144734064172225919985153153736244302459328) * 
(t + 1733149324186367358509713307996813388922147363320953556627453856871464344817) * 
(t + 63058247527559997808754465715771715540382722221120268489624945332318694664669)


可以推出（注意负号）：
X1=-1733149324186367358509713307996813388922147363320953556627453856871464344817
X2=-63058247527559997808754465715771715540382722221120268489624945332318694664669
"""

由于 $t=t_1^x$，直接上离散对数。

1
2
3
4
U1=-1733149324186367358509713307996813388922147363320953556627453856871464344817
U2=-63058247527559997808754465715771715540382722221120268489624945332318694664669
discrete_log(U1,Mod(t1,p))
#59164940663412913403923154565404322432501032178958345904039356200875940871519

然后验证一下，发现正确结果比实际解出来的值多 1。

1
2
print(M**59164940663412913403923154565404322432501032178958345904039356200875940871519)
print(M**59164940663412913403923154565404322432501032178958345904039356200875940871520)

因此得到：

1
2
index=59164940663412913403923154565404322432501032178958345904039356200875940871520
prime=75400000000000000000000000000000000000000000000000000000000000000000000000001

其实感觉构造 $p\equiv 11 {\text{ or }} 19\pmod{20}$ 的素数可能更好，因为这样可以满足 $p \equiv 3 \pmod 4$，开平方根有公式。

5.AES-Plus

Meet in the middle 攻击，枚举两个密钥共 $16^2$ 种组合，对已知明文加密 16 次，已知密文解密 16 次。得到使用的两个密钥分别是 4 和 11，然后

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
from Crypto.Util.number import *
from Crypto.Cipher import AES
from tqdm import *
flagC=long_to_bytes(0xba099276411c24b734948053cea63b4f)
knownP=long_to_bytes(0xd66fe087038cf381d3bcfe6bcf8c6a1b)
knownC=long_to_bytes(0x6a0b644af7b11a267f8b97399e8bee39)

def aes_encrypt(key: bytes, data: bytes) -> bytes:
    cipher = AES.new(key, AES.MODE_ECB)
    return cipher.encrypt(data)

def aes_decrypt(key: bytes, data: bytes) -> bytes:
    cipher = AES.new(key, AES.MODE_ECB)
    return cipher.decrypt(data)

DIC={}
TABLE="0123456789abcdef"
KEYPRF="SUSCTF-AESPLUS-"
for i in range(0,4):# 我开了4个，分别是0~3，4~7，8~11，12~15，四个一起跑的。
    for j in range(16):
        print(i,j)
        DIC={}
        key1=(KEYPRF+TABLE[i]).encode()
        key2=(KEYPRF+TABLE[j]).encode()
        
        
        for encid in tqdm(range(1<<16)):
            m=knownP
            for bitno in range(16):
                bit=(1<<bitno)&encid
                if(bit):
                    m=aes_encrypt(key1,m)
                else:
                    m=aes_encrypt(key2,m)
            DIC[m]=encid
        for decid in tqdm(range(1<<16)):
            c=knownC
            for bitno in range(15,-1,-1):
                bit=(1<<bitno)&decid
                if(bit):
                    c=aes_decrypt(key1,c)
                else:
                    c=aes_decrypt(key2,c)
            if(DIC.get(c,-1)!=-1):
                print('decid=',decid)
                print('encid=',DIC.get(c,-1))
                print('i=',i)
                print('j=',j)
print(len(list(DIC)))

for i in range(3):
    input()
"""
第二个程序（4-7）的跑出来了结果：
encid=7896
decid=51186
i=4
j=11
"""

然后解密就有flag了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from Crypto.Util.number import *
from Crypto.Cipher import AES
from tqdm import *
def aes_encrypt(key: bytes, data: bytes) -> bytes:
    cipher = AES.new(key, AES.MODE_ECB)
    return cipher.encrypt(data)

def aes_decrypt(key: bytes, data: bytes) -> bytes:
    cipher = AES.new(key, AES.MODE_ECB)
    return cipher.decrypt(data)

encid=7896#0b0000101101111000#7896
decid=51186
ID=(decid<<16)|encid
key1=b"SUSCTF-AESPLUS-4"
key2=b"SUSCTF-AESPLUS-b"

flagC=long_to_bytes(0xba099276411c24b734948053cea63b4f)

knownC=long_to_bytes(0x6a0b644af7b11a267f8b97399e8bee39)
c=flagC
#c=knownC
for bitno in range(31,-1,-1):
    bit=(1<<bitno)&ID
    if(bit):
        c=aes_decrypt(key1,c)
    else:
        c=aes_decrypt(key2,c)
print(c.hex())
#6c524b66b5434c85b73da8e2e768a9ce

6.nfsr1

给出30组挑战，问你给出的字符串是随机生成的，还是经过NFSR处理过的。

注意到NFSR会将一个16字节的内容变成 32 字节，其主要代码如下：

1
2
3
4
5
6
7
8
def __call__(self, msg: bytes):
    enc = list()
    for m in msg:
        if self.lfsr0(1):
            enc += [m & self.lfsr1(8), m | self.lfsr1(8)]
        else:
            enc += [m | self.lfsr1(8), m & self.lfsr1(8)]
    return bytes(enc)

很显然，bitor 操作大概率会导致数值中 1 比特增加，bitand 操作大概率回导致数值中 1 比特减少，写个函数测试一下：

1
2
3
4
5
6
7
def calc(hexlv):
    Q = 0
    for i in range(16):
        x1 = int(hexlv[4*i:4*i+2], 16)
        x2 = int(hexlv[4*i+2:4*i+4], 16)
        Q += abs(bitcount(x1)-bitcount(x2))
    return Q/16

发现随机生成的字符串中， 函数值多为一点几，最高不超过2.25。而处理过的字符串函数值均超过了3。

那就直接上exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
from pwn import *
from hashlib import sha256
from Crypto.Util.number import *
from os import urandom
from gmpy2 import iroot
from Crypto.Cipher import AES
from tqdm import *


def getyanzhengma(s16len, s64len):
    LTSNMS = "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789"
    assert len(s16len) == 12 and len(s64len) == 64
    for i1 in LTSNMS:
        for i2 in LTSNMS:
            for i3 in LTSNMS:
                for i4 in LTSNMS:
                    if sha256((i1+i2+i3+i4+s16len).encode()).hexdigest() == s64len:
                        return i1+i2+i3+i4


def bitcount(x):
    c = 0
    while(x):
        c += (x & 1)
        x >>= 1
    return c


def calc(hexlv):
    Q = 0
    for i in range(16):
        x1 = int(hexlv[4*i:4*i+2], 16)
        x2 = int(hexlv[4*i+2:4*i+4], 16)
        Q += abs(bitcount(x1)-bitcount(x2))
    return Q/16


sh = remote('game.ctf.seusus.com', 57317)

cc = sh.recvline(keepends=False)
s64 = cc[-64:].decode()
s16 = cc[12:24].decode()
print(cc)
print(s64)
print(s16)
yanzhengma = getyanzhengma(s16, s64)
print(yanzhengma)
sh.recvuntil(b':')
sh.sendline(yanzhengma.encode())

for i in (range(30)):
    print('Round ', i, ':')
    sh.recvuntil(b':')
    datarecv = sh.recvline(keepends=False).strip().decode()
    print(datarecv)
    judg = calc(datarecv)
    print(judg)
    sh.recvuntil(b'>')
    if(judg > 2.5):
        sh.sendline(b'1')
    else:
        sh.sendline(b'0')

sh.interactive()

7.signin_in_sys

7x01 solution

一个卡了我一坤天的题。一开始弄了个乱搞做法，60%概率能过 256 的上限。然后自己推式子推了好久，终于把 128 的上限过掉了。。。。

这个题首先注意到算法其实是 DSA 签名算法，没有出现共用随机数的情况，但使用的H函数有点奇怪，并且注意力涣散的人也可以注意到 H(s)=H('\x00'+s) 。

题目要求是求出sus_hex的一组合法签名，但一开始不知道sus_hex的值，需要通过hint，而hint就需要求出验证公钥。根据上面我注意到的内容，构造 00 和 0000，这两个的 H 值一样。

设 $A$ 是相同的 $H$ 值，根据 $r_i\equiv g^{k_i}\pmod p$ 和 $s_i\equiv\dfrac{A+xr_i}{k_i} \pmod q,i=1,2$，可以解出
$$
g^x= \left(\dfrac{r_1^{s_1}}{r_2^{s_2}}\right)^{(r_1-r_2)^{-1} \bmod q} \bmod p
$$
(有点复杂，但反正指数上的东西全模 $q$，不是指数上的东西全模 $p$ 就行)。

拿到 pk 后，就可以拿到sus_hex。

放一下求这一部分的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
dat=sh.recvline(keepends=False)
p,q,g,t=eval(dat)
print(p)
print(q)
print(g)
print(t)

sh.recvuntil(b'>')
sh.sendline(b's')
sh.recvuntil(b'>')
sh.sendline(b'0000')
sh.recvuntil(b') =')
r1,s1=eval(sh.recvline(keepends=False))
print(r1,s1)


sh.recvuntil(b'>')
sh.sendline(b's')
sh.recvuntil(b'>')
sh.sendline(b'00000000')
sh.recvuntil(b') =')
r2,s2=eval(sh.recvline(keepends=False))
print(r2,s2)

cpk=pow(r1,s1,p)*inverse(pow(r2,s2,p),p)%p
pk=pow(cpk,inverse(r1-r2,q),p)
print(pk)

sh.recvuntil(b'>')
sh.sendline(b'h')
sh.recvuntil(b'>')
sh.sendline(str(pk).encode())
sh.recvuntil(b'=')
Msghex=sh.recvline(keepends=False).strip()[1:-1]
assert len(Msghex)==256
print(Msghex)

sh.interactive() #后面直接手搓了

再关注一下这个 $H$ 函数，可以发现由于 $m_i$ 很小，因此 $h \oplus m_i$ 可以写成 $h+\delta_i$，其中 $\delta_i$ 也很小。把异或换加，就可以发现，最后 $H$ 可以写成一个关于 $t$ 的多项式，其中 $\delta_i $ 很小 。

1
2
3
4
5
6
# sage
# notice that ^^ in sage means xor, ^ in sage means power, ^ in python means xor.
def H( m: bytes):
    h = 0
    for mi in m :
        h = (h ^^ mi) * t % q

下面就以 $n=4$ 举例了，其实 $n=128$ 同理。
$$
H(m)\equiv \delta_1t^4+\delta_2t^3+\delta_3t^2+\delta_4t\pmod q \tag {8.1}
$$

若目标字符串的 hash 值为 $D$，则 $(8.1)$ 可以写成
$$
D\equiv \delta_1t^4+\delta_2t^3+\delta_3t^2+\delta_4t\pmod q \tag {8.2}
$$
去同余，得
$$
\delta_1t^4+\delta_2t^3+\delta_3t^2+\delta_4t-D-k q =0\tag {8.3}
$$
然后就可以构造LLL：

1

中间的矩阵是 $(n+2)$ 行 $(n+3)$ 列的，因此对中间的矩阵LLL之后，找到一个倒数第三个数是 $1$，最后一个数是 $0$ 的行向量，就可以解出来了。

这个常数 $K$ 其实是根据闵可夫斯基定理，要保证格中的向量足够大（原理很玄学，有时候必须加，不加可能求不出正确结果）。这里取的是 $K=2^{900}$，注意到最后一列是 $0$ ，所以乘上一个 $K$ 不影响结果。

下面是LLL部分代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#SAGE
#!/usr/bin/env python
# coding: utf-8

# In[1]:

from Crypto.Util.number import *
from random import *
q=244309567133428459339052233620763590631
t=139116278922633292045835908998748980746
n=128
mmm=long_to_bytes(0x6532303734613033336462373133663863653039303532636265316338306631393031356163336534386136646664313433303636623330373637663931326633343331323133643539383064646136643131663361613831663639663139656533623033383033303332623734633063343632663635323834373631346132)
C=[]   #这个C是以前乱搞用的，这里被废弃了
def H( m: bytes):
    h = 0
    for mi in m :
#       C.append((h&(2**300-256))|0x55) 
        h = (h ^^ mi) * t % q
    return h
D=(H(mmm))
print(D)
#86818520128168117392109372309780328095

# In[2]:
def getVec(mod,g,targ):
    K=2**900
    M=[[0 for _ in range(n+3)] for __ in range(n+2)]
    for i in range(n+2):
        M[i][i]=1
    for i in range(n):
        M[i][n+2]=Integer(pow(g,n-i,mod))*K
    M[n][n+2]=-targ*K
    M[n+1][n+2]=mod*K
    M=matrix(ZZ,M)
    return M.LLL()
A=getVec(q,t,D)
print(A[0]) #a0不符合要求
vv=A[0]
for i in range(n+2):
    if(A[i][-3]==1):
        vv=A[i]
        break
print(vv)
#(-3, -1, 1, -2, 2, -2, -1, -1, 1, 0, 1, 1, -1, 4, 2, -1, -1, -1, 1, -2, 1, -2, 2, 3, -3, -3, 1, 0, 2, -2, -2, 0, -1, 1, 1, 3, 2, 1, 1, -2, -1, 0, -1, 1, -2, 0, -2, 0, -1, 0, 0, 0, -1, 1, 1, -1, 1, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
#(3, -5, 1, 2, -4, -1, 1, -2, 1, -3, 0, 0, -1, -2, 1, 3, 2, 1, 4, 2, 0, 0, 3, -2, -1, 4, 0, 1, -2, -1, 0, -1, 3, 1, 0, -1, -3, -1, -1, 1, 1, 1, 0, 0, -1, 3, 2, 0, 1, 0, 1, -1, 1, -2, -1, 2, -1, -1, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0)

# In[3]:
R=vv if vv[0]>=0 else -vv
s=[]
h=0
for i in range(128):
    ich=((h+R[i])^^h)
    s.append(ich)
    h=(h+R[i])*t%q
print(s)
print(h,D)
#[3, 5, 1, 2, 28, 15, 15, 2, 1, 29, 0, 0, 1, 2, 1, 3, 2, 1, 12, 6, 0, 0, 5, 6, 1, 12, 0, 3, 2, 3, 0, 1, 13, 3, 0, 1, 5, 3, 1, 31, 3, 31, 0, 0, 1, 5, 6, 0, 7, 0, 1, 1, 1, 14, 15, 2, 1, 3, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
#86818520128168117392109372309780328095 86818520128168117392109372309780328095

# In[4]:
bytes(s).hex()
#030501021c0f0f02011d00000102010302010c0600000506010c0003020300010d0300010503011f031f00000105060007000101010e0f02010300000000000001000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000


7x02 乱搞做法，60% 概率能过 $m_i< 256$，但基本过不掉本题的 $128$

其实一开始我的想法是看sus_hex在求hash 的时候对应的 $\delta$，然后构造一组差值，LLL后首行就是解，但这么做其实并不太对，因为 原本的 $\delta$ 再加上得到的 $\vec v$ 可能会超掉。（比如 h&0xff=82，但 $\delta+v=-83$，也就是对应的字符值超过了 $256$。

然后我就搞了一个非常玄学的做法，根据三重循环，枚举向量，找一个符合要求的字符串，甚至还能以 60% 的概率过 $m_i<256$ 的上界。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#python 3
from sage.all import *
from Crypto.Util.number import *
from random import *
from os import urandom
from tqdm import *
def SOLVE(q,t,mmm,mode=1):
    n=128
    C=[]
    def recH( m: bytes):
        h = 0
        for mi in m :
            C.append((h^mi)-h)
            h = (h ^ mi) * t % q
        return h
    def H( m: bytes):
        h = 0
        for mi in m :
            h = (h ^ mi) * t % q
        return h
    msg=recH(mmm)
    def getVec(mod,g):
        K,n=2^900,128
        M=[[0 for _ in range(n+2)]for __ in range(n+1)]
        for i in range(n+1):
            ge=ZZ(pow(g,n-i,mod))
            M[i][i]=1
            M[i][n+1]=ZZ(ge*K)
        M[n][n+1]=ZZ(K*mod)
        M=matrix(ZZ,M)
        if(mode==1):
            padC=C+[0]*500
            listm=list(M)
            listm.append(padC[:n+2])
            M=matrix(listm)
        A=M.LLL()
        return A[0],A[1],A[2]
    A0,A1,A2=getVec(q,t)
    def check(v):
        C2=[(C[i]+v[i]) for i in range(n)] 
        s=''
        h=0
        for i in range(n):
            ich=((h+C2[i])^h)
            if(ich>127 or ich<0):
                return 0
            ch=chr(ich)
            s+=ch
            h=int(int(h) +int(C2[i])) * t % q
        return 1
    finded=0
    for i in tqdm(range(-30,30)):
        for j in range(-30,30):
            for k in range(-30,30):
                if(i==0 and j==0 and k==0):
                    continue
                b=i*A0+j*A1+k*A2
                if(check(b)):
                    finded=True
                    break
            if(finded):
                break
        if(finded):
            break
    C2=[(C[i]+b[i]) for i in range(n)] 
    s=[]
    h=0
    try:
        for i in range(n):
            ch=((h+C2[i])^h)
            s.append(ch)
            h=int(int(h) +int(C2[i])) * t % q
        return bytes(s).hex()
    except:
        return None

8.goodwell(赛后补题)

一个AES-GCM.nonce-reuse的题目，需要先注意到safe_random 每32轮就重复一次，因此存在nonce-reuse。

这边放一下重用部分的代码，注意是在Sage中运行的，因此 ^^ 是异或，^ 是乘幂，GHASH给出了GCM校验的过程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#In [1]:
from Crypto.Cipher import AES
from Crypto.Util.number import *
def encrypt(data, nonce):
    cipher = AES.new(key, AES.MODE_GCM, nonce)
    return nonce + cipher.encrypt(data) + cipher.digest()
def decrypt(data):
    cipher = AES.new(key, AES.MODE_GCM, data[:16])
    return cipher.decrypt_and_verify(data[16:-16], data[-16:])
def xor(s1, s2): # used to attack aes-ctr
    if(len(s1) == 1 and len(s1) == 1):
        return bytes([ord(s1) ^ ord(s2)])
    else:
        return bytes(x ^^ y for x, y in zip(s1, s2))
enonce=b'9ijn8uhb7ygv6tfc'
key=b'1qaz2wsx3edc4rfv'
ciph1=encrypt(b"prefixprefixprefix66666666",enonce)
ciph2=encrypt(b"prefixprefixprefix88888888",enonce)
C1=ciph1[16:-16]
T1=ciph1[-16:]
C2=ciph2[16:-16]
T2=ciph2[-16:]
print(C1)
print(T1)
print(C2)
print(T2)
C3=xor(b'123456',xor(b'prefix',C1[:6]))
print(C3.hex())
print(enonce.hex())
#Out [1]:
b"\x12\xc5=J'\x9c)\xf4\x96\xd1\x1e=LX\xc81D\x95\xd9:\xf3\xf6\x01\x8e\xa5 "
b'-\xb0h\xf8\x82/}\xa9\x84\nE`L}]o'
b"\x12\xc5=J'\x9c)\xf4\x96\xd1\x1e=LX\xc81D\x95\xd74\xfd\xf8\x0f\x80\xab."
b'\x10\x03l\x9d\x84^\x98\xf4\x05\xaf\x19\xae$\xb1\xc6w'
53856b187bd2
39696a6e387568623779677636746663
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#In [2]:
F.<t>=GF(2**128,modulus=(([1,1,1,0,0,0,0,1]+[0]*500)[:128]+[1]))
R.<x>=PolynomialRing(F)
def convert_to_blocks(ciphertext):
    return [ciphertext[i:i + 16] for i in range(0 , len(ciphertext), 16)]
def b2p(block, a):
    if len(block) != 16:
        block = block + b"\0" * (16 - len(block))
    poly = 0 
    bin_block = bin(bytes_to_long(block))[2:].zfill(128)
    for i in range(len(bin_block)):
        poly += a**i * int(bin_block[i])
    return poly
def p2b(poly):
    return long_to_bytes(int(bin(poly.integer_representation())[2:].zfill(128)[::-1], 2))
def GHASH(C,T=b""):
    Cb=convert_to_blocks(C)
    Cp= [b2p(Cb[i], t) for i in range(len(Cb))]
    Tp=b2p(T,t)
    L = struct.pack(">QQ", 0 * 8, len(C) * 8)
    Lp = b2p(L, t)
    G = 0
    for i in range(len(Cb)):
        G=(G+Cp[i])*x
    G=(G+Lp)*x+Tp
    return G
G1=GHASH(C1,T1)
G2 =GHASH(C2, T2)
G3 =GHASH(C3)
print(G1)
print(G2)
print(G3)
#Out [2]:
(t^127 + t^123 + t^122 + t^116 + t^113 + t^112 + t^108 + t^107 + t^105 + t^101 + t^100 + t^97 + t^95 + t^93 + t^92 + t^91 + t^90 + t^86 + t^85 + t^84 + t^83 + t^79 + t^75 + t^73 + t^72 + t^70 + t^69 + t^67 + t^64 + t^61 + t^59 + t^58 + t^57 + t^56 + t^55 + t^52 + t^50 + t^45 + t^44 + t^43 + t^40 + t^39 + t^38 + t^37 + t^34 + t^30 + t^28 + t^25 + t^23 + t^21 + t^20 + t^19 + t^18 + t^15 + t^13 + t^9 + t^8 + t^6 + t^3)*x^3 + (t^74 + t^71 + t^69 + t^66 + t^64 + t^62 + t^61 + t^60 + t^56 + t^55 + t^46 + t^45 + t^43 + t^42 + t^41 + t^40 + t^39 + t^38 + t^35 + t^34 + t^33 + t^32 + t^30 + t^28 + t^27 + t^26 + t^23 + t^20 + t^19 + t^17 + t^16 + t^15 + t^13 + t^11 + t^8 + t^5 + t)*x^2 + (t^123 + t^121 + t^120)*x + t^127 + t^126 + t^125 + t^124 + t^122 + t^121 + t^119 + t^117 + t^116 + t^115 + t^113 + t^111 + t^109 + t^108 + t^107 + t^106 + t^105 + t^101 + t^100 + t^97 + t^90 + t^89 + t^87 + t^85 + t^81 + t^78 + t^76 + t^69 + t^64 + t^63 + t^60 + t^58 + t^56 + t^55 + t^53 + t^52 + t^51 + t^50 + t^49 + t^47 + t^46 + t^45 + t^44 + t^42 + t^38 + t^32 + t^28 + t^27 + t^26 + t^25 + t^24 + t^20 + t^18 + t^17 + t^11 + t^10 + t^8 + t^7 + t^5 + t^4 + t^2
(t^127 + t^123 + t^122 + t^116 + t^113 + t^112 + t^108 + t^107 + t^105 + t^101 + t^100 + t^97 + t^95 + t^93 + t^92 + t^91 + t^90 + t^86 + t^85 + t^84 + t^83 + t^79 + t^75 + t^73 + t^72 + t^70 + t^69 + t^67 + t^64 + t^61 + t^59 + t^58 + t^57 + t^56 + t^55 + t^52 + t^50 + t^45 + t^44 + t^43 + t^40 + t^39 + t^38 + t^37 + t^34 + t^30 + t^28 + t^25 + t^23 + t^21 + t^20 + t^19 + t^18 + t^15 + t^13 + t^9 + t^8 + t^6 + t^3)*x^3 + (t^78 + t^77 + t^76 + t^74 + t^71 + t^70 + t^68 + t^66 + t^64 + t^56 + t^55 + t^54 + t^53 + t^52 + t^44 + t^43 + t^42 + t^41 + t^40 + t^39 + t^37 + t^36 + t^35 + t^34 + t^33 + t^32 + t^29 + t^27 + t^26 + t^23 + t^22 + t^21 + t^19 + t^17 + t^16 + t^15 + t^13 + t^11 + t^8 + t^5 + t)*x^2 + (t^123 + t^121 + t^120)*x + t^127 + t^126 + t^125 + t^123 + t^122 + t^121 + t^118 + t^117 + t^113 + t^112 + t^111 + t^107 + t^106 + t^104 + t^101 + t^98 + t^94 + t^93 + t^92 + t^90 + t^88 + t^87 + t^84 + t^83 + t^79 + t^78 + t^77 + t^76 + t^74 + t^72 + t^71 + t^69 + t^61 + t^59 + t^58 + t^57 + t^56 + t^52 + t^51 + t^48 + t^46 + t^45 + t^44 + t^43 + t^41 + t^37 + t^32 + t^31 + t^29 + t^28 + t^27 + t^24 + t^21 + t^20 + t^18 + t^17 + t^15 + t^14 + t^3
(t^46 + t^43 + t^41 + t^40 + t^39 + t^38 + t^36 + t^35 + t^34 + t^33 + t^28 + t^27 + t^23 + t^22 + t^20 + t^18 + t^17 + t^15 + t^13 + t^8 + t^7 + t^6 + t^3 + t)*x^2 + (t^123 + t^122)*x
1
2
3
4
5
6
7
8
9
10
11
12
13
14
#In [3]:
P=G1+G2
print(P)
auth_keys = [r for r, _ in P.roots()]
print(auth_keys)
for H, _ in P.roots():
    EJ = G1(H)
    T3 = G3(H) + EJ
    print("H: " + str(H) + "\nT3: " + str(p2b(T3).hex()))
#Out [3]:
(t^78 + t^77 + t^76 + t^70 + t^69 + t^68 + t^62 + t^61 + t^60 + t^54 + t^53 + t^52 + t^46 + t^45 + t^44 + t^38 + t^37 + t^36 + t^30 + t^29 + t^28 + t^22 + t^21 + t^20)*x^2 + t^124 + t^123 + t^119 + t^118 + t^116 + t^115 + t^112 + t^109 + t^108 + t^105 + t^104 + t^100 + t^98 + t^97 + t^94 + t^93 + t^92 + t^89 + t^88 + t^85 + t^84 + t^83 + t^81 + t^79 + t^77 + t^74 + t^72 + t^71 + t^64 + t^63 + t^61 + t^60 + t^59 + t^57 + t^55 + t^53 + t^50 + t^49 + t^48 + t^47 + t^43 + t^42 + t^41 + t^38 + t^37 + t^31 + t^29 + t^26 + t^25 + t^21 + t^15 + t^14 + t^11 + t^10 + t^8 + t^7 + t^5 + t^4 + t^3 + t^2
[t^126 + t^124 + t^123 + t^116 + t^114 + t^110 + t^109 + t^108 + t^106 + t^102 + t^101 + t^99 + t^98 + t^94 + t^92 + t^90 + t^88 + t^87 + t^82 + t^80 + t^77 + t^75 + t^73 + t^72 + t^67 + t^64 + t^63 + t^62 + t^61 + t^60 + t^59 + t^58 + t^52 + t^50 + t^49 + t^48 + t^46 + t^43 + t^42 + t^40 + t^38 + t^37 + t^36 + t^32 + t^31 + t^26 + t^25 + t^21 + t^19 + t^17 + t^16 + t^15 + t^12 + t^8 + t^5 + 1]
H: t^126 + t^124 + t^123 + t^116 + t^114 + t^110 + t^109 + t^108 + t^106 + t^102 + t^101 + t^99 + t^98 + t^94 + t^92 + t^90 + t^88 + t^87 + t^82 + t^80 + t^77 + t^75 + t^73 + t^72 + t^67 + t^64 + t^63 + t^62 + t^61 + t^60 + t^59 + t^58 + t^52 + t^50 + t^49 + t^48 + t^46 + t^43 + t^42 + t^40 + t^38 + t^37 + t^36 + t^32 + t^31 + t^26 + t^25 + t^21 + t^19 + t^17 + t^16 + t^15 + t^12 + t^8 + t^5 + 1
T3: 2b10dad9688ea6dab1b06fbdea3db46b
1
2
3
4
5
#In [4]:
A=enonce.hex()+C3.hex()+'2b10dad9688ea6dab1b06fbdea3db46b'
decrypt(bytes.fromhex(A))
#Out [4]:
b'123456'

9.nfsr2 (赛后补题，Update 10.24)

2024.10.24补题，最终能够做到概率性地成功恢复lfsr的seed。

P.S. 该题为错题，和出题人讨论了一下，任务中的andNum和orNum应该取同一个值，否则会出现多解（见我最后的图片）。

不过还是很想吐槽一下这个题，以前我也见过两三个LFSR题用 getrandbits 然后题目越做越复杂的。呃，为啥不用 getPrime 或者 ((1<<(nbits-1))+1)|getrandbits(nbits) 来保证一下最高位和最低位都是 $1$ 呢。

其实这个题主要考察LFSR的状态转移表示为 $\mathrm{GF}(2)$ 上的矩阵方程，比如一个 4 阶的LFSR，其表达式为 $y=x_4\oplus x_2\oplus x_1$，那么其转移矩阵如下：

9-1

因此，对于任意初始状态向量（种子） $\vec v \neq \vec 0$，执行 $k$ 次LFSR之后，其状态为 $\vec v\mathbf M^{k}$。

继续看一下题目中附件：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# util.py
nbit = 128
def bitcount(x):
    c=0
    while(x):
        c+=(x&1)
        x>>=1
    return c
class LFSR:
    def __init__(self, seed: int, mask: int):
        self.state = seed & (2**nbit - 1)
        self.mask = mask & (2**nbit - 1)

    def __next__(self):
        out = bitcount(self.state & self.mask) & 1
        self.state = ((self.state << 1) | out) & (2**nbit - 1)
        return out
    
    def __call__(self, bits: int):
        out = 0
        for _ in range(bits):
            out = (out << 1) | next(self)
        return out

class NFSR:
    def __init__(self, lfsr0: LFSR, lfsr1: LFSR):
        self.lfsr0 = lfsr0
        self.lfsr1 = lfsr1
    
    def __call__(self, msg: bytes):
        enc = list()
        for m in msg:
            if self.lfsr0(1):
                enc += [m & self.lfsr1(8), m | self.lfsr1(8)]
            else:
                enc += [m | self.lfsr1(8), m & self.lfsr1(8)]
        return bytes(enc)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#task.py
import secrets
from utils import nbit, LFSR, NFSR

def proof_of_work():
    import string, hashlib, random

    alphabet = string.ascii_letters + string.digits
    proof = ''.join(random.choices(alphabet, k=16))
    digest = hashlib.sha256(proof.encode()).hexdigest()

    print(f"sha256(XXXX+{proof[4:]})=={digest}")
    x = input("Give me XXXX:")
    h = hashlib.sha256((x + proof[4:]).encode()).hexdigest()
    return h == digest

assert proof_of_work()
print("Good luck")
try:
    for i in range(5):
        seeds = [secrets.randbits(nbit) for _ in range(2)]
        masks = [secrets.randbits(nbit) for _ in range(2)]
        lfsrs = [LFSR(seed, mask) for seed, mask in zip(seeds, masks)]
        nfsr = NFSR(*lfsrs)

        msg = secrets.token_bytes(200)
        enc = nfsr(msg)

        print(f"Round {i+1}: {enc.hex()}")
        print(f"{masks = }")
        if not bytes.fromhex(input('>')) == msg:
            raise Exception
    flag = open('/flag', 'r').read()
    print(f"Congratulations: {flag}")
except:
    print("Not this time")

这一次很明显，长度为 $200$ 字节的信息加密后变成了长度为 $400$ 的内容，对于字节 $m$，执行 m&x 和 m|y，并且两个lfsr的mask已知，要求求出原始信息，5 轮获得flag。因此，可以根据每一组输出两字节的 $1$ 比特数量来确定 bitand 和 bitor 的结果。

注：bitcount(m|x)==bitcount(m|y) 的概率其实很低，因为我一开始没注意到这个转移矩阵，因此遇到这种情况我直接跳过了。其实可以将对应的位置标记为 ?，到时候利用转移矩阵，在 mask 已知的情况下，知道 $n$ 个输出就可以恢复LFSR，这 $n$ 个比特的输出其实不需要连续。因此，lfsr0还是非常容易恢复的

然后是恢复LFSR1，LFSR1累计输出了 $3200$ 比特，消息一共 $1600$ 比特。然后密文的 $3200$ 比特有LFSR1输出和消息 bitand,bitor 得到。因此根据下面的知识，可以得到 $1/4$ 的LFSR1输出和 $1/2$ 的明文内容：

  1. 若 m|x 对应位为 $0$ ，则 $m$ 和 $x$ 的对应位均为 $0$。
  2. 若 m&x 对应位 为 $1$，则 $m$ 和 $x$ 的对应位均为 $1$。

期望情况下，能够得到约 $800$ 个LFSR1 输出的值和 $800$ 个明文比特。先将未知内容全部标记为 ?，然后根据上面两条规则逐步确定，然后取不为 ? 的值构造矩阵即可。

这样就有可能能够恢复两个LFSR的seed了，但由于这两个LFSR可能不满秩，因此可能需要进行一些微操。

P.S：八阶LFSR基于的多项式 $x^8+x^4+x^3+x^2+1$ 中，假设里面状态是 $b_8b_7b_6b_5b_4b_3b_2b_1$，是 $8,4,3,2$ 四个数异或，那个 $1$ 才是多余的！（你可以理解为每移位一次相当于乘一个 $x$，最后的 $1$ 属于输出结果的系数）。因此，$\mathrm{lowbit(mask)\ne1}$不影响，但最mask的高位不为 $1$ 则会导致LFSR失秩。

具体本地解题代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
#solve.py
import random
from Testans import *
from Testinput import *
from utils import *
from sage.all import *


def lowbit(x):
    return ((x) & (-x))


def bitcount(x):
    count = 0
    while(x):
        count += 1
        x ^= ((x) & (-x))
    return count


T = 125 #T表示数据的编号，有的数据不一定能运行起来。
nfsr = NFSR(None, None)
m0, m1 = maskRec0[T], maskRec1[T]
nfsr.lfsr0 = LFSR(0, m0)
nfsr.lfsr1 = LFSR(0, m1)
ciph = hexEnc[T]
output = []
outstat0 = ''
for i in range(200):
    op1, op2 = int(ciph[4*i:4*i+2], 16), int(ciph[4*i+2:4*i+4], 16)
    output.append((op1, op2))
for op1, op2 in output:
    assert(bitcount(op1) != bitcount(op2))
    if(bitcount(op1) > bitcount(op2)):
        outstat0 += '0'
    else:
        outstat0 += '1'
realLen0 = m0.bit_length()
btn0 = m0 & (-m0)
cur0 = int(outstat0[:realLen0], 2)
inistat0 = ''
for i in range(128):
    curt = cur0 & 1
    cur0 >>= 1
    preb = (bitcount(cur0 & m0) ^ curt) & 1
    inistat0 = str(preb)+inistat0
    cur0 |= (preb << (realLen0-1))
    # print(cur0)
bciph = list(('0'*3200+(bin(int(ciph, 16))[2:]))[-3200:])
msg = ['?']*1600
outstat1 = ['?']*3200

for i in range(200):
    msg8ind = 8*i
    or8ind, and8ind = 16*i, 16*i+8
    if(outstat0[i] == '1'):
        or8ind, and8ind = 16*i+8, 16*i
    for j in range(8):
        if(bciph[or8ind+j] == '0'):
            msg[msg8ind+j] = '0'
            outstat1[or8ind+j] = '0'
        if (bciph[and8ind+j] == '1'):
            msg[msg8ind+j] = '1'
            outstat1[and8ind+j] = '1'


realLen1 = m1.bit_length()+1-(m1 & (-m1)).bit_length()
M = [[i == (j+1) for j in range(realLen1)]for i in range(realLen1)]
realm1 = m1//lowbit(m1)
for i in range(realLen1):
    M[realLen1-1-i][-1] = ((realm1) & (1 << i)) != 0
M = Matrix(GF(2), M)
A = []
vecb = []
for i in range(len(outstat1)):
    if(outstat1[i] != '?'):
        vecb.append(int(outstat1[i]))
        xpi = (i+(lowbit(m1).bit_length()))
        # print(i,xpi)
        Mcur = (M**xpi).T
        A.append(list(Mcur)[-1])
    if(len(A) == realLen1):
        break

A = Matrix(GF(2), A)
vecb = vector(GF(2), vecb)
Ainv = (A.T)**(-1)
inistat1v = (vecb*Ainv)

inistat1s = ''
for i in range(len(inistat1v)):
    inistat1s += str(inistat1v[i])

for i in range(1, lowbit(m1).bit_length()):
    inistat1s += str(inistat1v*(M**i)[-1])

inistat1 = int(inistat1s, 2)
inistat0 = int(inistat0, 2)
print(lowbit(m0), lowbit(m1))
print(inistat0, inistat1)
print(seed0Rec[T], seed1Rec[T])
nfsr.lfsr0.state = inistat0
nfsr.lfsr1.state = inistat1

#begin test part#
# sb=bytes.fromhex(hexMsg[T])
# print(len(sb),sb)
# C1=ciph
# C2=nfsr(sb).hex()
# print(C1==C2)
#end test part#

testout0 = []
testout1 = []
for i in range(200):
    judg = nfsr.lfsr0(1)
    out1a = nfsr.lfsr1(8)
    out1b = nfsr.lfsr1(8)
    testout0.append(judg)
    testout1.append((out1a, out1b))


def getByte(andNum, andRes, orNum, orRes):
    for x in range(256):
        if((x & andNum) == andRes and (x | orNum) == orRes):
            return x
    return -1


def getByte2(andNum, andRes, orNum, orRes, pipeistr=None):
    C = []
    for x in range(256):
        if((x & andNum) == andRes and (x | orNum) == orRes):
            C.append(x)
    return C


for i in range(5): #没做到最后了，输出5个，看看多解的情况吧。
    pipeis = ''.join(msg[i*8:i*8+8])
    print(pipeis)
    o1, o2 = testout1[i]
    r1, r2 = output[i]
    print(o1, o2, r1, r2)
    if(testout0[i] == 0):
        print(testout0[i], (getByte2(o2, r2, o1, r1)),
              int(hexMsg[T][i*2:i*2+2], 16))
    else:
        print(testout0[i], (getByte2(o1, r1, o2, r2)),
              int(hexMsg[T][i*2:i*2+2], 16))

送一个数据生成器的代码，数据生成器的输出文件可以直接被上述代码import。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#datagen.py
import secrets
from utils import nbit, LFSR, NFSR
from tqdm import *
print("Generating Data...")
hexEnc=[]
maskRec0=[]
maskRec1=[]
hexMsg=[]
seed0Rec=[]
seed1Rec=[]
try:
    for i in tqdm(range(300)):
        seeds = [secrets.randbits(nbit) for _ in range(2)]
        masks = [secrets.randbits(nbit) for _ in range(2)]
        lfsrs = [LFSR(seed, mask) for seed, mask in zip(seeds, masks)]
        nfsr = NFSR(*lfsrs)

        msg = secrets.token_bytes(200)
        enc = nfsr(msg)
        hexEnc.append(enc.hex())
        maskRec0.append(masks[0])
        maskRec1.append(masks[1])
        hexMsg.append(msg.hex())
        seed0Rec.append(seeds[0])
        seed1Rec.append(seeds[1])
        with open(f'Testinput.py','w') as f:
            f.write(f'{hexEnc=}\n')
            f.write(f'{maskRec0=}\n')
            f.write(f'{maskRec1=}\n')
            f.write(f'{seed0Rec=}\n')
            f.write(f'{seed1Rec=}\n')
        with open(f'Testans.py','w') as f:
            f.write(f"{hexMsg=}\n")

except:
    print("Not this time")

最终运行结果，可以发现最后出现了多解，而正确明文的值恰好是其中一个解，因此本题概率性地恢复了seed也算是做成功了。

9-2

10. 总结

两年没打CTF了，以前一起打CTF的队友基本上都找到了很好的工作，不过还好，自己也最终靠着4.43的GPA保研到了SEU，也算是大学卷G.卷了3年的结果吧。

大四保研后，前前后后玩了12个城市，东南西北都跑了一趟，也算是玩得尽兴了吧。现在觉得电子游戏就是一堆数据，在南京玩和出南京旅游都没意思了，继续开卷！

在研究生阶段，能够在SUS继续和志同道合的朋友一起打CTF，讨论技术，其实也挺不错的，争取把CTF捡回来。

考虑到自己读博概率不高，因此研 1 先以做项目和打竞赛为主吧。研 2 争取能发 2 篇论文（哎，没科研经历保研是真伤，面试时老师问了我很多很难的密码学问题，我都答上来了，结果SEU优营还没进前100，最后递补上了学硕）笑死，去年SEU保研穿了，今年保研又穿了，300+名的一个学妹递补上了。

CTFSeason4
#WriteUp
SUSCTF2024
http://example.com/2024/10/23/SUSCTF2024/
作者
huangx607087
发布于
2024年10月23日
许可协议