BlockCipher4

huangx607087学习分组密码的笔记4

0.About

38个月过去了，终于从 3 更新到 4 了，好耶！！

因为0xGame出了一个简单的两轮DES差分，之前密码学课程中也讲了DES差分，因此自己决定尝试自行探索一下DES的差分攻击

Review:你当年写这个的时候，应该不会意识到3和4之间隔了多久吧

4. DES的差分攻击

4o01 DES的差分攻击简介

DES在 8 轮迭代之后，其原本明文的统计规律已经消失，并且扩散性达到了最好。为何DES还要设计成 16 轮呢？原因就在于，8轮DES很容易受到差分攻击。

我们来回顾一下单轮DES的Festial结构：E扩展、P置换、轮密钥加、S盒四个部分，其中只有S盒为非线性部分，其余均为线性部分，可以根据已知内容去逆推。而差分攻击，就是构建两个明文 $M_1$ 和 $M_2$，加密后得到 $C_1$ 和 $C_2$，根据 $M_1\oplus M_2$ 和 $C_1\oplus C_2$ 的值，尝试反推 $K$ 的值。而差分攻击之所以能够起作用，其原因就是 $S$ 盒的不均匀性。下图显示了 $S_1$ 的差分情况，可以看出：当 $S_0$ 两个输入异或值为 $01\text{H}$ 时，有 $6/64$ 的概率两个输出的异或值为 $3$，$2/64$ 的概率两个输出的异或值为 $5$，$12/64$ 的概率输出 $\mathrm{10}$。而当 $S_0$ 的两个输入异或值为 $\mathrm{34H}$ 时，两个输出异或值为 $2$ 的概率达到了 $16/64$。因此，差分攻击属于选择明文攻击，需要加密机才能实现。

p.s. 本博文十六进制数均会出现 $\mathrm{0x}$ 前缀或 $\mathrm H$ 后缀，若无前后缀标明的，则均按照十进制看待。$S$ 盒编号取值为 $0\sim 7$。

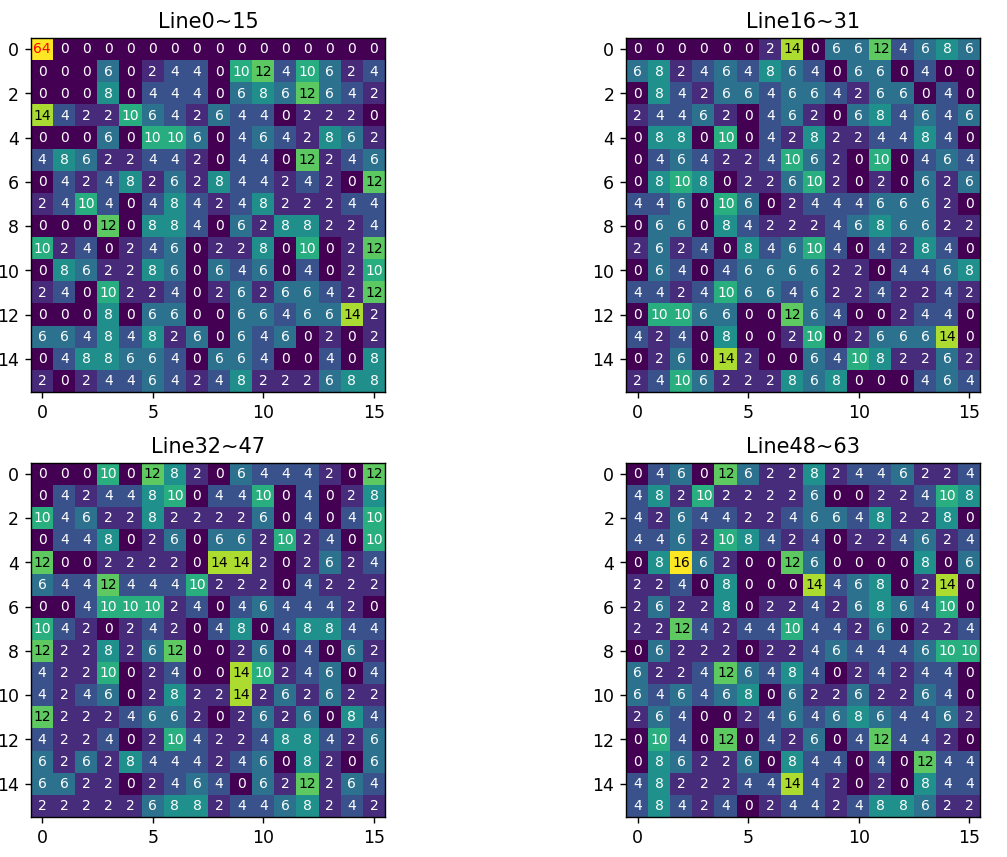
我们以 $S_0$ 盒输入差分为 $01\text H$ 为例，经过实验，可以得到下面的内容：也就是当 $S_0$ 0输出差分值为 $3$ 时，可能的输入值（不是输入差分）为 $29,61,60,28,45,44$ 这六种（仔细的人可以注意到：每一组内都存在异或值为 $1$ 的一对数，因为你的输入差分为 $1$）。

3:{29, 61, 60, 28, 45, 44}
5:{6, 7}
6:{37, 12, 13, 36}
7:{50, 51, 22, 23}
9:{40, 41, 14, 15, 16, 17, 54, 55, 56, 57}
10:{4, 5, 38, 39, 48, 49, 20, 21, 52, 53, 58, 59}
11:{32, 33, 2, 3} 
12:{8, 9, 46, 47, 18, 19, 24, 25, 26, 27}
13:{34, 35, 10, 11, 62, 63}
14:{0, 1}
15:{42, 43, 30, 31}

因此，我们可以使用下面的代码，构造： int detSCnt[8][64][16] 和 set<int> detSREC[8][64][16]。其中：detSCnt[i][j][k] 表示第 $i$ 个 $S$ 盒输入差分为 $j$ ，输出差分为 $k$ 的情况数量。 detSREC[i][j][k] 表示第 $i$ 个 $S$ 盒，输入差分为 $j$，输出差分为 $k$ 时所有可能的输入值构成的集合。例如： $\mathtt{detSCnt[0][1][3]=6}$，$\mathtt{detSRec[0][1][3]}={29,61,60,28,45,44}$。显然，有 $\mathtt{|detSRec[i][j][k]|=detSCnt[i][j][k]}$。

detSCnt=[[[0 for k in range(16)]for j in range(64)]for i in range(8)]
detSRec=[[[set() for k in range(16)]for j in range(64)]for i in range(8)]
def getS(sid,val):
    v1,v2=2*(not not (val&32))+(val&1),(val>>1)&15
    return S[sid][v1][v2]
def calcS():
    for i in range(8):
        for j in range(64):
            for k in range(64):
                in1,in2=j,k 
                out1,out2=getS(i,in1),getS(i,in2)
                detin=j^k
                detout=out1^out2
                detSCnt[i][detin][detout]+=1
                detSRec[i][detin][detout]|=set([j])

4o02 0xGame2024 DES的实现代码

后面我们以 0xGame 2024 那个简化版DES为例，这里没有考虑初始置换盒轮密钥的生成，但其实加上这两个过程，本质也一样。因为这两个过程仍然是线性变换。

#Util.py
from functools import reduce
from operator import add
from random import Random

__s_box = [[[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7], [0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8], [4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0], [15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13]], 
           [[15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10], [3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5], [0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15], [13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9]], 
           [[10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8], [13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1], [13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7], [1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12]], 
           [[7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15], [13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9], [10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4], [3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14]], 
           [[2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9], [14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6], [4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14], [11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3]], 
           [[12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11], [10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8], [9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6], [4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13]], 
           [[4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1], [13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6], [1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2], [6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12]], 
           [[13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7], [1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2], [7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8], [2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11]]]
__ep = [31, 0, 1, 2, 3, 4, 3, 4, 5, 6, 7, 8, 7, 8, 9, 10, 11, 12, 11, 12, 13, 14, 15, 16, 15, 16, 17, 18, 19, 20, 19, 20, 21, 22, 23, 24, 23, 24, 25, 26, 27, 28, 27, 28, 29, 30, 31, 0]
__p = [15, 6, 19, 20, 28, 11, 27, 16, 0, 14, 22, 25, 4, 17, 30, 9, 1, 7, 23, 13, 31, 26, 2, 8, 18, 12, 29, 5, 21, 10, 3, 24]
def EP(data):
    return [data[x] for x in __ep]
def P(data):
    return [data[x] for x in __p]
def S_box(data):
    output = []
    for i in range(0, 48, 6):
        row = data[i] * 2 + data[i + 5]
        col = reduce(add, [data[i + j] * (2 ** (4 - j)) for j in range(1, 5)])
        output += [int(x) for x in format(__s_box[i // 6][row][col], '04b')]
    return output
def bytes2bin(m):
    return [int(i) for i in bin(int(m.hex(), 16))[2:].zfill(8 * len(m))]
def bin2bytes(m):
    return int(''.join([str(i) for i in m]), 2).to_bytes(length=len(m)//8, byteorder='big')
def encrypt(plain, key,nrd=2): #这边以前没有nrd参数，也给加上了，以前就是 2 轮。
    pt = bytes2bin(plain)
    sub_key = bytes2bin(key)
    L, R = pt[:32], pt[32:]
    for i in range(nrd):
        prev_L = L
        L = R
        expanded_R = EP(R)
        xor_result = [a ^ b for a, b in zip(expanded_R, sub_key)]
        substituted = S_box(xor_result)
        permuted = P(substituted)
        R = [a ^ b for a, b in zip(permuted, prev_L)]
    cipher = R + L
    return bin2bytes(cipher)
def decrypt(cipher, key,nrd=2):
    ct = bytes2bin(cipher)
    sub_key = bytes2bin(key)
    L, R = ct[:32], ct[32:]
    for i in range(nrd):
        prev_L = L
        L = R
        expanded_R = EP(R)
        xor_result = [a ^ b for a, b in zip(expanded_R, sub_key)]
        substituted = S_box(xor_result)
        permuted = P(substituted)
        R = [a ^ b for a, b in zip(permuted, prev_L)]
    cipher = R + L
    return bin2bytes(cipher)
# 以下内容0xGame原题没有，为作者自加内容
S = __s_box.copy()
__pinv = [8, 16, 22, 30, 12, 27, 1, 17, 23, 15, 29, 5, 25, 19, 9,0, 7, 13, 24, 2, 3, 28, 10, 18, 31, 11, 21, 6, 4, 26, 14, 20]
def Pinv(data):
    return [data[x] for x in __pinv]

4o02 2轮DES

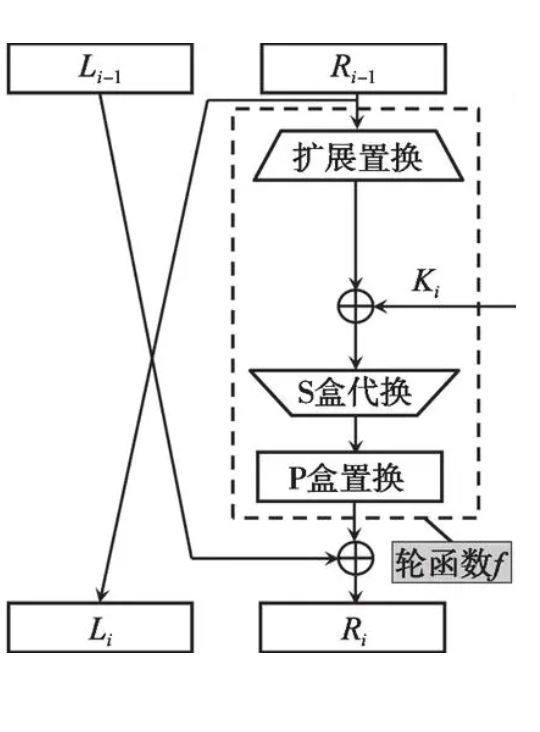
对于两轮DES而言，若输入 $(L_0,R_0)$ ，可以得到输出为 $(R_0,R_1)$，然后第二轮得到输入 $(R1,R_2)$，最后交换一下得到密文为 $R_2||R_1$。

由于最后有 $R_1$ 的存在，因此其安全性和一轮 DES 没有差别。

而已知 $L_0,R_0,R_1$ 时，考虑到最后一步存在 $\oplus L_0$ 的操作，因此在一轮中，可以直接构造 $L_0=00000000\mathrm H$。这样最后一步就可以被我们忽略掉了。

假设构造 (00000000H,00000000H) 和 (00000000H,12345678H) 两个明文。由于 $E$ 置换是确定的，因此有
$$
E(\mathtt{00000000H})=\mathtt{000000000000H}=\mathtt{00H,00H,00H,00H,00H,00H,00H,00H}
$$

$$
E(\mathtt{12345678H})=\mathtt{0A41A82AC3F0H}=\mathtt{02H,24H,06H,28H,0AH,2CH,0FH,30H}
$$

因此，经过 E 扩展后，上下异或，可以得到XOR前的差分为 $\mathtt{02H,24H,06H,28H,0AH,2CH,0FH,30H}$

由于异或的Key是一样的，因此经过轮密钥加后，S 盒的输入差分也为 $\mathtt{02H,24H,06H,28H,0AH,2CH,0FH,30H}$。

假设密钥为 $\mathtt{76AD5C3FFB2EH}=\mathtt{2EH,2CH,3FH,0FH,1CH,35H,2AH,1DH}$（这个我们不知道）。但一轮加密后，我们可以得到两组数据： $(R_0,R_1)=\mathtt{00000000H,3213371EH}$ 和 $(R_0,R_1)=\mathtt{12345678H,86C32DB5H}$。因为我们 XOR 的 $L_0$ 为全 $0$，因此将两个 $R_1$ 进行 $P^{-1}$ 置换，可以得到 $R_0=\mathtt{00000000H}$ 对应的 $S$ 盒输出内容为 $\mathtt{34E41D72H}$，$R_0=\mathtt{12345678H}$ 对应的 $S$ 盒输出内容为 $\mathtt{84F321B7H}$，两个做异或，得到 $S$ 盒差分值为 $\mathtt{B0173CC5H}$。这也顺序对应了八个 $S$ 盒各自的输出差分值。

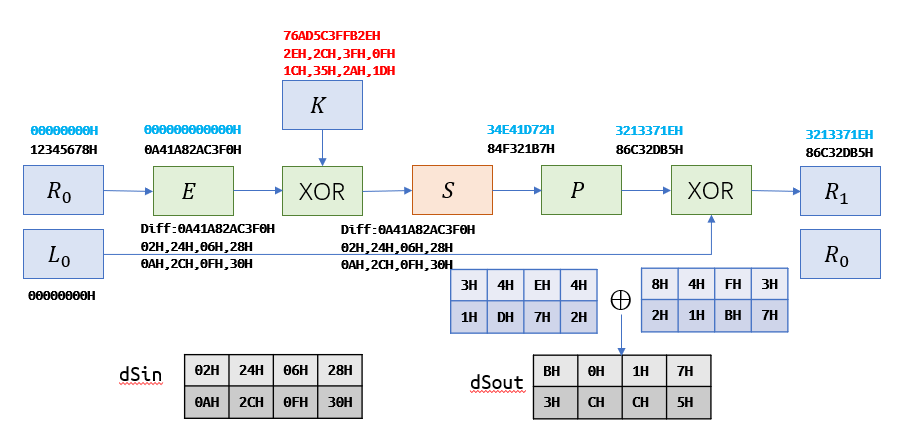
然后我们就可以进行查表：以 $S_0$ 为例：detSRec[0][0x02][0xB]={63,61,40,42,29,31}，而 $S_0$ 的 输入内容为 $\mathtt{02H}$ 。对这里面所有的内容异或输入内容$\mathtt{02H}$，可以得到 0x02 xor detSRec[0][0x02][0xB]={61,63,42,40,31,29}。同理，其他的七个 $S$ 盒的相关内容也能够被推出来。比如在下图中，我们得到了 $K$ 的第 $0\sim5$ 位的六个候选值和 $6\sim11$ 位的十个候选值。多次选取，取交集，就可以得到最后可能的密钥 $K$ 了。

特别提醒：推密钥的时候，考虑的不是输入差分，是输入内容！这里因为构造了全0的明文，输入差分就是输入内容，此处巧起来了，这里一定要考虑输入的内容，因为只有知道输入内容，才能尝试获取密钥！！！对输入差分的使用体现在了我们的数组下标里面。

0xGame原题是十次机会，但其实完全够用了，下面是两轮攻击的脚本。

from Util import *
from random import *
from os import urandom
from Crypto.Util.number import *
detSCnt=[[[0 for k in range(16)]for j in range(64)]for i in range(8)]
detSRec=[[[set() for k in range(16)]for j in range(64)]for i in range(8)]
def getS(sid,val):
    v1,v2=2*(not not (val&32))+(val&1),(val>>1)&15
    return S[sid][v1][v2]

def calcS():
    for i in range(8):
        for j in range(64):
            for k in range(64):
                in1,in2=j,k 
                out1,out2=getS(i,in1),getS(i,in2)
                detin=j^k
                detout=out1^out2
                detSCnt[i][detin][detout]+=1
                detSRec[i][detin][detout]|=set([j])


def getrandpair(x):
    a=getrandbits(64)
    b=a^x
    return a,b

calcS()
myKey=urandom(6)
Aarr=[0x00000000,0x22222222,0x44444444,0x88888888,0x11111111,0x12481248,0x84218421,0xedb7edb7,0xffffffff]
n=len(Aarr)
M=[Aarr[i].to_bytes(8,byteorder='big') for i in range(len(Aarr))]
C=[]
for i in range(n):
    C.append(encrypt(M[i],myKey))
bC=[]
for i in range(n):
    cval=bytes_to_long(C[i])
    bC.append(((cval&0xffffffff).to_bytes(4,byteorder='big'),(cval>>32).to_bytes(4,byteorder='big')))

Sinput=[]
for i in range(n):
    beforeS=M[i][4:]
    beforeS=bytes_to_long(bin2bytes(EP(bytes2bin(beforeS))))
    arr=[]
    for j in range(8):
        arr.append(beforeS&63)
        beforeS>>=6
    Sinput.append(arr[::-1])
Soutput=[]
for i in range(n):
    afterE=C[i][4:]
    afterE=bytes_to_long(bin2bytes(Pinv(bytes2bin(afterE))))
    arr=[]
    for j in range(8):
        arr.append(afterE&15)
        afterE>>=4
    Soutput.append(arr[::-1])
import copy
dSoutput=copy.deepcopy(Soutput)
for i in range(n-1,-1,-1):
    for j in range(8):
        dSoutput[i][j]^=dSoutput[0][j]
print(Sinput)
print(dSoutput)
K=[]
for i in range(8):
    D=set(list(range(64)))
    for j in range(1,n):
        x=Sinput[j][i]
        y=dSoutput[j][i]
        dtmp=list(detSRec[i][x][y])
        ctmp=[i^x for i in dtmp]
        D&=set(ctmp)
    K.append(list(D))
print(K)
keyguess=0
for i in range(8):
    keyguess<<=6
    keyguess|=K[i][0]
print(hex(keyguess)[2:],myKey.hex())

可能的输出结果，最后一行为猜测密钥和实际密钥，可以看出是正确的：

Sinput=dSinput=[[0, 0, 0, 0, 0, 0, 0, 0], [4, 4, 4, 4, 4, 4, 4, 4], [8, 8, 8, 8, 8, 8, 8, 8], [17, 17, 17, 17, 17, 17, 17, 17], [34, 34, 34, 34, 34, 34, 34, 34], [2, 36, 9, 16, 2, 36, 9, 16], [48, 8, 4, 3, 48, 8, 4, 3], [61, 27, 54, 47, 61, 27, 54, 47], [63, 63, 63, 63, 63, 63, 63, 63]]
dSoutput=[[0, 0, 0, 0, 0, 0, 0, 0], [3, 7, 13, 6, 13, 14, 7, 7], [10, 10, 10, 11, 14, 9, 10, 12], [13, 3, 12, 4, 0, 4, 0, 6], [10, 9, 0, 8, 0, 0, 6, 6], [12, 11, 13, 14, 7, 8, 3, 3], [11, 10, 13, 10, 7, 9, 7, 0], [2, 1, 8, 6, 5, 13, 13, 1], [1, 13, 6, 1, 0, 9, 13, 7]]
[[13], [44], [16], [13], [40], [61], [12], [7]]
36c40da3d307 36c40da3d307

4o03 3轮DES

进入三轮 DES，我们可以知道 $R_2$ 和 $R_3$ 的值，这个时候，我们就需要开始重视 $E$ 扩展了。 $E$ 扩展是将每组 4bit 和前一组的最后一bit、后一组的最高一bit结合。也就是

1	`PQRS ABCD WXYZ --> ZPQRSA SABCDW DWXYZP`

因此，为了每次只影响一个 $S$ 盒的输出，我们可以选择 $S$ 盒的输入差分为 $4,8,12$ （这个 $12$ 没有加任何前后缀哦），对应的十六进制位为 $2,4,6$。下面我们继续以 $S_0$ 为例：

1
2
3

detSCnt[0][4]=[0, 0, 0, 6, 0, 10, 10, 6, 0, 4, 6, 4, 2, 8, 6, 2]
detSCnt[0][8]=[0, 0, 0, 12, 0, 8, 8, 4, 0, 6, 2, 8, 8, 2, 2, 4]
detSCnt[0][12]=[0, 0, 0, 8, 0, 6, 6, 0, 0, 6, 6, 4, 6, 6, 14, 2]

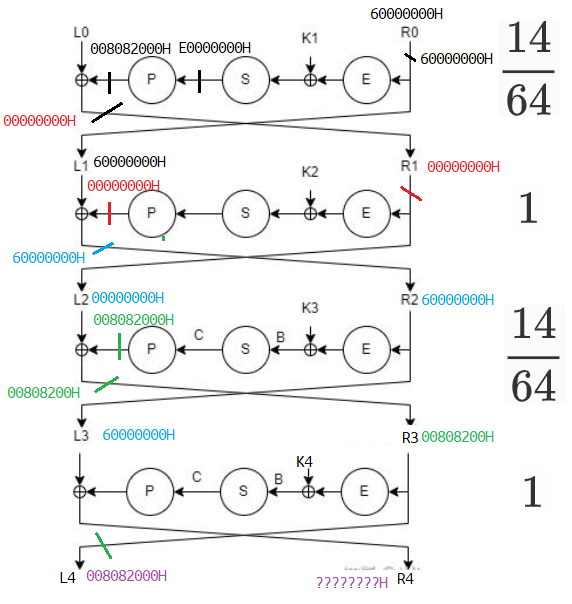
可以看到，当 $S_0$ 输入差分为 $\mathtt{0CH}$ 时，输出差分为 $\mathtt{EH}$ 的概率最高，为 $14/64$。而当 $S_0$ 输出差分值 $\mathtt{EH}$ 时，对应输出差分为 $\mathtt{E0000000H}$，经过 $P$ 盒置换，得到 $\mathtt{00808200H}$。然后这个 $\mathtt{00808200H}$ 还要和 $L_0$ 异或。

因此，可以构造 $(L_0,R_0)=\mathtt{(00808200H,60000000H)}$，这样在第一轮结束后，第二轮输入的 $R_1$ 差分为全 $0$，这样 $R_2$ 在异或前的差分就是全 $0$，异或后，可以有 $R_2=\mathtt{60000000H}$。

分析每一步的概率：第一轮输入差分 $(L_0,R_0)=\mathtt{(00808200H,60000000H)}$，输出差分为 $\mathtt{60000000H,00000000H}$ 的概率为 $14/64$，第二轮输入差分 $\mathtt{60000000H,00000000H}$，输出差分 $\mathtt{00000000H,60000000H}$ 的概率为 $1$，第三轮输入差分 $\mathtt{00000000H,60000000H}$，输出差分 $\mathtt{60000000H,XXXXXXXXH}$ 的概率为 $1$。因此，询问 $5$ 次差不多就能有一次符合条件的结果。至于输出差分不符合期望的情况，我们直接丢弃，重新询问。

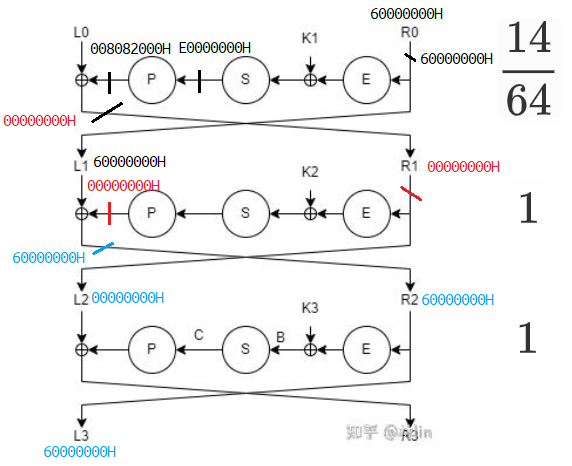
因此，最后我们只需要找到 $R_2=\mathtt{60000000H}$ 的输出即可，对于其他 $S$ 盒也一样，这边给出一组参考数据吧：

S盒的参考值如下：
S0  0ch eh 14/64 00808200h 60000000h  00808200h=P(e0000000h)
S1  08h ah 16/64 40080000h 04000000h  40080000h=P(0a000000h)
S2  04h 9h 12/64 04000100h 00200000h  ... ... ... ... ... ..
S3  04h 7h 12/64 80401000h 00020000h
S4  0ch 3h 10/64 20000080h 00006000h
S5  08h 6h 16/64 00200008h 00000400h
S6  0ch ch 14/64 00100001h 00000060h
S7  04h 7h 12/64 00020820h 00000002h

所以三轮的代码如下：

from Util import *
from random import *
from os import urandom
from Crypto.Util.number import *
from datetime import *
detSCnt=[[[0 for k in range(16)]for j in range(64)]for i in range(8)]
detSRec=[[[set() for k in range(16)]for j in range(64)]for i in range(8)]
def getS(sid,val):
    v1,v2=2*(not not (val&32))+(val&1),(val>>1)&15
    return S[sid][v1][v2]

def calcS():
    for i in range(8):
        for j in range(64):
            for k in range(64):
                in1,in2=j,k 
                out1,out2=getS(i,in1),getS(i,in2)
                detin=j^k
                detout=out1^out2
                detSCnt[i][detin][detout]+=1
                detSRec[i][detin][detout]|=set([j])
#bin2bytes(P(bytes2bin(bytes.fromhex('00070000')))).hex()

def getrandpair(x):
    a=getrandbits(64)
    b=a^x
    return a,b
def l2b(x,l=-1):
    bs=long_to_bytes(x)
    if(len(bs)<l):
        bs=bytes([0]*(l-len(bs)))+bs
    return bs

calcS()
myKey=urandom(6)#b'F(x)=x'
xorNum=[0x0080820060000000,0x4008000004000000,0x0400010000200000,0x8040100000020000,
        0x2000008000006000,0x0020000800000400,0x0010000100000060,0x0002082000000002]
numxe=[(0x0c,0xe),(0x08,0xa),(0x04,0x9),(0x04,0x7),
       (0x0c,0x3),(0x08,0x6),(0x0c,0xc),(0x04,0x7)]

tStart=datetime.now()
totalQuery=0
K=[None for _ in range(8)]
for T in range(8):
    NCipher=7
    Aarr=[]
    while len(Aarr)<NCipher:
        totalQuery+=1
        a,b=getrandpair(xorNum[T])
        ba,bb=l2b(a,8),l2b(b,8)
        x,y=encrypt(ba,myKey,3),encrypt(bb,myKey,3)
        ix,iy=bytes_to_long(x),bytes_to_long(y)
        if(((ix^iy)&0xffffffff)==(xorNum[T]&0xffffffff)):
            Aarr.append((ba,bb))
    Sinput=[]
    for i in range(NCipher):
        r2,r3=Aarr[i][1][4:],Aarr[i][1][:4]
        eb=bin2bytes(EP(bytes2bin(r2)))
        ebi=bytes_to_long(eb)
        tmparr=[]
        for j in range(8):
            tmparr.append(ebi&0x3f)
            ebi>>=6
        Sinput.append(tmparr[::-1])
    sarr=detSRec[T][numxe[T][0]][numxe[T][1]]
    D=set(range(64))
    for i in range(NCipher):
        s0=Sinput[i][T]
        xarr=set([s0^i for i in sarr])
        D=D&xarr
    K[T]=D

testM=urandom(8)
testC=encrypt(testM,myKey,3)
totalQuery+=1
guessKey=None
def dfs(step,keyarr):
    global guessKey
    if(step==8):
        keyval=0
        for i in range(8):
            keyval<<=6
            keyval|=keyarr[i]
        key2=int.to_bytes(keyval,6,byteorder='big')
        cc=encrypt(testM,key2,3)
        if(cc==testC):
            guessKey=key2
        return
    for i in K[step]:
        dfs(step+1,keyarr+[i])
dfs(0,[])
print(guessKey.hex(),myKey.hex(),guessKey==myKey)
if(guessKey==myKey):
    
    print(f'Success with queryed {totalQuery} times')
else:
    print('Fail')
tEnd=datetime.now()
print(f'Time Cost:{tEnd-tStart}')

一个可能的运行结果：

1
2
3

fd31f37d571f fd31f37d571f True
Success with queryed 407 times
Time Cost:0:00:00.225095

4o04 4轮DES

对于 4 轮 DES 而言，其在 3 轮上面又多了一轮，我们之前已知，输入差分为 $\mathtt{60000000H}$ 时，输出差分为 $\mathtt{00808200H}$ 的概率为 $14/64$，因此我们在第三轮的基础上，继续考虑这 $14/64$的概率：输出 $R_3=\mathtt{00808200H}$ 。这样，大约每 $21$ 次查询，就可以获得一次满足$L_4=R_3=\mathtt{00808200H}$ 的情况。

攻击代码：

from Util import *
from random import *
from os import urandom
from Crypto.Util.number import *
from datetime import *
detSCnt=[[[0 for k in range(16)]for j in range(64)]for i in range(8)]
detSRec=[[[set() for k in range(16)]for j in range(64)]for i in range(8)]
def getS(sid,val):
    v1,v2=2*(not not (val&32))+(val&1),(val>>1)&15
    return S[sid][v1][v2]

def calcS():
    for i in range(8):
        for j in range(64):
            for k in range(64):
                in1,in2=j,k 
                out1,out2=getS(i,in1),getS(i,in2)
                detin=j^k
                detout=out1^out2
                detSCnt[i][detin][detout]+=1
                detSRec[i][detin][detout]|=set([j])
def getrandpair(x):
    a=getrandbits(64)
    b=a^x
    return a,b
def l2b(x,l=-1):
    bs=long_to_bytes(x)
    if(len(bs)<l):
        bs=bytes([0]*(l-len(bs)))+bs
    return bs

calcS()
myKey=urandom(6)
xorNum=[0x0080820060000000,0x4008000004000000,0x0400010000200000,0x8040100000020000,
        0x2000008000006000,0x0020000800000400,0x0010000100000060,0x0002082000000002]
T=0
totalQuery=0
NCipher=5
tStart=datetime.now()
K=[set(range(64))for i in range(8)]
for T in range(8):
    Aarr=[]
    Carr=[]
    while(len(Aarr)<NCipher):
        totalQuery+=1
        a,b=getrandpair(xorNum[T])
        ba,bb=l2b(a,8),l2b(b,8)
        x,y=encrypt(ba,myKey,4),encrypt(bb,myKey,4)
        ix,iy=bytes_to_long(x),bytes_to_long(y)
        if(((ix^iy)&0xffffffff)==(xorNum[T]>>32)):
            Aarr.append((ba,bb))
            Carr.append((x,y))
    for i in range(5):
        r3,r4=Carr[i][1][4:],Carr[i][1][:4]
        r30,r40=Carr[i][0][4:],Carr[i][0][:4]
        dr4=bytes_to_long(r4)^bytes_to_long(r40)
        dr4^=xorNum[T]&0xffffffff
        bdr4=l2b(dr4,4)
        din=xorNum[T]>>32
        X=EP(bytes2bin(l2b(din,4)))
        dSin=[32*X[6*_]+16*X[6*_+1]+8*X[6*_+2]+4*X[6*_+3]+2*X[6*_+4]+X[6*_+5] for _ in range(8)]
        iSout=bytes_to_long(bin2bytes(Pinv(bytes2bin(bdr4))))
        dSout=[]
        r3Sin=[]
        r3E=EP(bytes2bin(r3))
        r3Sin=[32*r3E[6*_]+16*r3E[6*_+1]+8*r3E[6*_+2]+4*r3E[6*_+3]+2*r3E[6*_+4]+r3E[6*_+5] for _ in range(8)]
        for j in range(8):
            dSout.append(iSout&15)
            iSout>>=4
        dSout=dSout[::-1]
        for j in range(8):
            tmpset=list(detSRec[j][dSin[j]][dSout[j]])
            keyset=set([ts ^ r3Sin[j]for ts in tmpset])
            K[j]&=keyset
testM=urandom(8)
testC=encrypt(testM,myKey,3)
totalQuery+=1
guessKey=None

def dfs(step,keyarr):
    global guessKey
    if(step==8):
        keyval=0
        for i in range(8):
            keyval<<=6
            keyval|=keyarr[i]
        key2=int.to_bytes(keyval,6,byteorder='big')
        cc=encrypt(testM,key2,3)
        if(cc==testC):
            guessKey=key2
        return
    for i in K[step]:
        dfs(step+1,keyarr+[i])
print(f'K={K}')
dfs(0,[])
print(guessKey.hex(),myKey.hex(),guessKey==myKey)
if(guessKey==myKey):
    print(f'Success with queryed {totalQuery} times')
else:
    print('Fail')
tEnd=datetime.now()
print(f'Time Cost:{tEnd-tStart}')

一个可能的运行结果：

K=[{52}, {0}, {18}, {33}, {14}, {58}, {43}, {10}]
d004a13baaca d004a13baaca True
Success with queryed 2255 times
Time Cost:0:00:00.565169

5 到 8 轮的情况就很复杂了，等以后遇到题目再更新吧:(

CTFSeason4

#Notes

BlockCipher4

http://example.com/2024/11/06/BlockCipher4/

作者

huangx607087

发布于

2024年11月6日

许可协议

24Nov1 上一篇

SUSCTF2024 下一篇