24Nov4

huangx607087 11月的切题4

0.Introduction

11月月底，又做了几个题，然后 2 号考密码学，5 号考无线数字通信技术。两场考试考完，趁 6 号休息一天，整理一下之前做过的题目。

1.[强网拟态2024]brokenoracle

11月25日，向外校的师傅要了一个强网拟态的题目，感觉不是很难，但因为自己想简单了，所以本地搞还是用了 3 小时。

先看一眼题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
from Crypto.Util.number import *
from Crypto.Cipher import AES
from hashlib import sha256
import socketserver
import signal
import os
import string
import random
from Crypto.PublicKey import RSA
from Crypto.Util.number import getPrime,getStrongPrime
from Crypto.Random import get_random_bytes


class Task(socketserver.BaseRequestHandler):
    def _recvall(self):
        BUFF_SIZE = 4096
        data = b''
        while True:
            part = self.request.recv(BUFF_SIZE)
            data += part
            if len(part) < BUFF_SIZE:
                break
        return data.strip()

    def send(self, msg, newline=True):
        try:
            if newline:
                msg += b'\n'
            self.request.sendall(msg)
        except:
            pass

    def recv(self, prompt=b'> '):
        self.send(prompt, newline=False)
        return self._recvall()

    def handle(self):
        p=getStrongPrime(512)
        q=getStrongPrime(512)
        e=65537
        n=p*q
        phi=(p-1)*(q-1)
        d=pow(e,-1,phi)
        token=os.urandom(1000//8)
        c=pow(bytes_to_long(token),e,n)
        self.send(b"n=")
        self.send(hex(n).encode())
        
        self.send(b"your token is")
        self.send(hex(c).encode())
        
        signal.alarm(60)
        for i in range(100):
            self.send(b"give me your message to decrypt")
            c=self.recv()
            try:
                c=int(c,16)
            except:
                self.send(b"wrong!")
                self.request.close()
                
            
            m=pow(c,d,n)
            brokenm=m&((2**(40)-1)*(2**492))
            self.send(hex(brokenm).encode())
        self.send(b"give me your token")
        t1=self.recv()
        if bytes.fromhex(t1.decode())==token:
            f=open("./flag","rb")#此部分本地复现时有所修改
            flag=f.read()
            f.close()
            self.send(flag)
        else:
            self.send(b"wrong! try again!")    
        self.request.close()


class ThreadedServer(socketserver.ThreadingMixIn, socketserver.TCPServer):
    pass


class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
    pass


if __name__ == "__main__":
    HOST, PORT = '0.0.0.0', 9999 #本地复现改成了60712端口，呃，自己本地复现一般从60709端口开始启用。
    print("HOST:POST " + HOST+":" + str(PORT))
    server = ForkedServer((HOST, PORT), Task)
    server.allow_reuse_address = True
    server.serve_forever()

很明显，这个题和 RSA ParityOracle类似，不过既不知道最高位，也不是知道最低位，当构造密文发过去之后，服务器会给你解密，并返回对应明文的 $40$ 比特内容，对应的位权为 $2^{492}\sim2^{531}$。时间限制 1min，查询限制 100 次。

既然这样，那就可以从Parity Oracle那里想。可以先本地写个代码测一下：

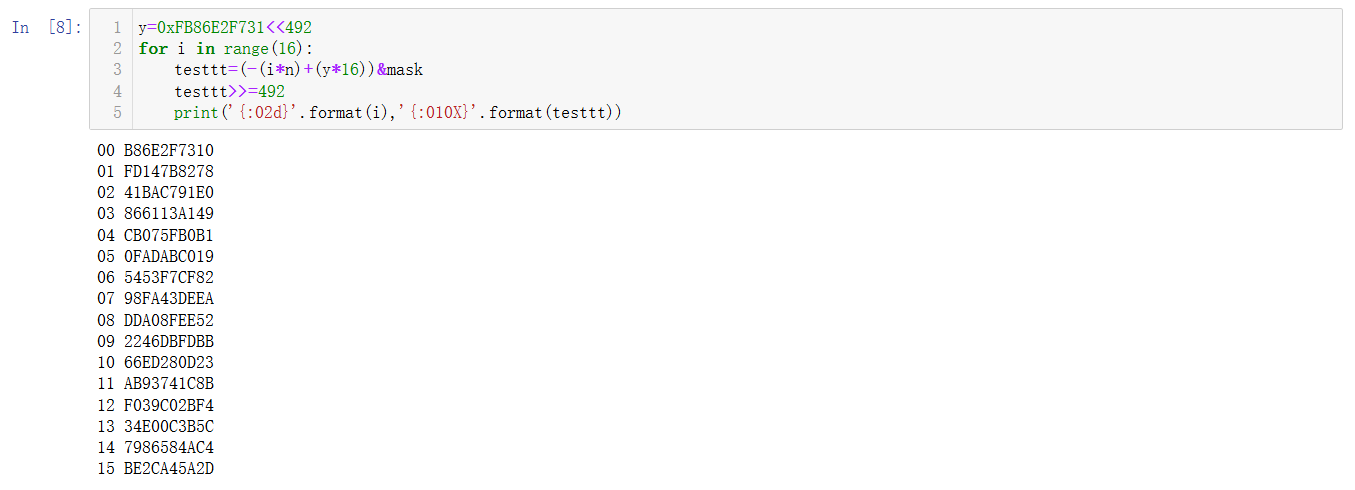
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from Crypto.Util.number import *
p=getStrongPrime(512)
q=getStrongPrime(512)
e=65537
n=p*q
phi=(p-1)*(q-1)
d=pow(e,-1,phi)
token=bytes_to_long(os.urandom(1000//8))
c=pow((token),e,n)
mask=(2**40-1)<<492
print('{:0256X}'.format(token))
def E(x):
    return int(pow(x,e,n))
def D(x):
    return int(pow(x,d,n))&mask
u=pow(16,e,n)
c0=c
for i in range(9):
    dc0=D(c0)
    dc0>>=492
    print('{:10X}'.format(dc0))
    c0=c0*u%n
#D887DFB86E
#887DFB86E2
#87DFB86E2F
#7DFB86E2F7
#DFB86E2F73
#FB86E2F731
#FD147B8278
#15EE0436F4
#B61FBFBC52

观察前6个数据，结果分别为：$\mathtt{D887DFB86EH,887DF86E2H,87DFB86E2FH,7DFB86E2F7H,DFB86E2F73H,FB86E2F731H}$。有很明显的移位特征，因为你对密文乘了个 $16^e$ 的系数，解密后明文也乘 $16$，对应到十六进制输出就是明显的移位特征。

由于 $t$ 是 $1000$ 位，$n$ 是 $1024$ 位，因此从第 $7$ 个数据开始，本应是 $\mathtt{B86E2F731XH}$，却变成了 $\mathtt{FD147B8278H}$，很明显，这应该是取模过的结果，也就是 $16^{6}t=xn+y$。这里把 $16^6t$ 写成了 $n$ 进制的格式，$x,y<n$。由于是乘了 $16$ 之后，才超过了 $n$，因此 $x$ 一定不超过 $15$。看看能不能搞出 $x$？

1

可以发现，这里 $x=1$，也就是这一次在取模前，数值为 $x$ 的一倍多，也就是 $\left \lfloor\dfrac{16^6t}{n} \right \rfloor=1$。

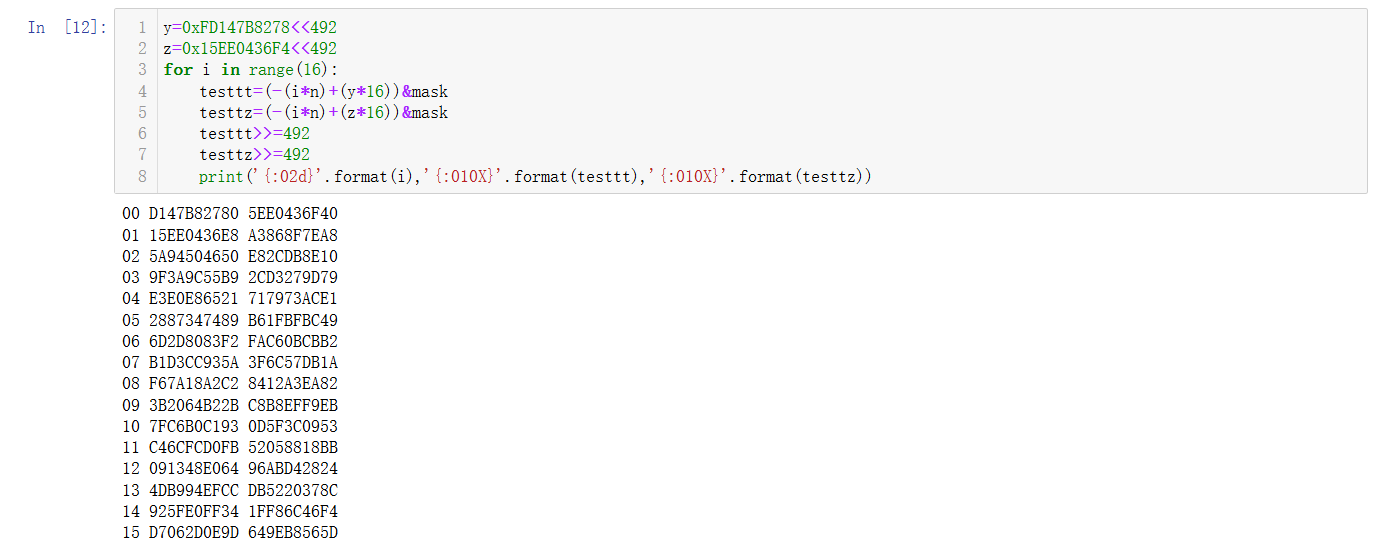
再测两组可以发现：$\mathtt{FD147B8278H}$ 变为 $\mathtt{15EE0436E8H}$ 对应的 $x$ 也是 $1$ ，和 $\mathtt{15EE0436F4H}$ 有很小的误差。同理，$\mathtt{15EE0436F4H}$ 变为 $\mathtt{B61FBFC52H}$ 对应的 $x $ 为 $5$ （实际计算为 $\mathtt{B61FBFC49H}$），也就是当 $t$ 再乘 $16$ 之后，$t$ 达到了 $n$ 的 $5$ 倍。

2

结合三个 $x$，大概可以知道：
$$
\left \lfloor\dfrac{16^8t}{n} \right \rfloor=277
$$
（其中 $277=\mathtt{115H}$）

因此，我们可以利用这个方法，求出 $\left \lfloor\dfrac{16^{k}t}{n}\right\rfloor$ 对应的值。这里会带有误差，但可以认为误差不超过 $16$ 就是正确的。不过问题是，如果想要获得一个非常精准的值，最后的值应该超过 $n$。并且你只有 $100$ 次机会，$16^{100}=2^{400}$，看来不太可行。

但可以利用这个方法，一次爆破三位十六进制数，即将上面所有的 $16$ 换成 $4096$，然后我们开一个数组 $M$，记录上个解密的有效状态，再开一个数组 $T$，代表 $\left \lfloor\dfrac{4096^{k}t}{n}\right\rfloor$ 结果的 $4096$ 进制表示。

最终本地测试代码如下，耗时只有两秒，估计就算对靶机应该也不会超过 5 秒吧：

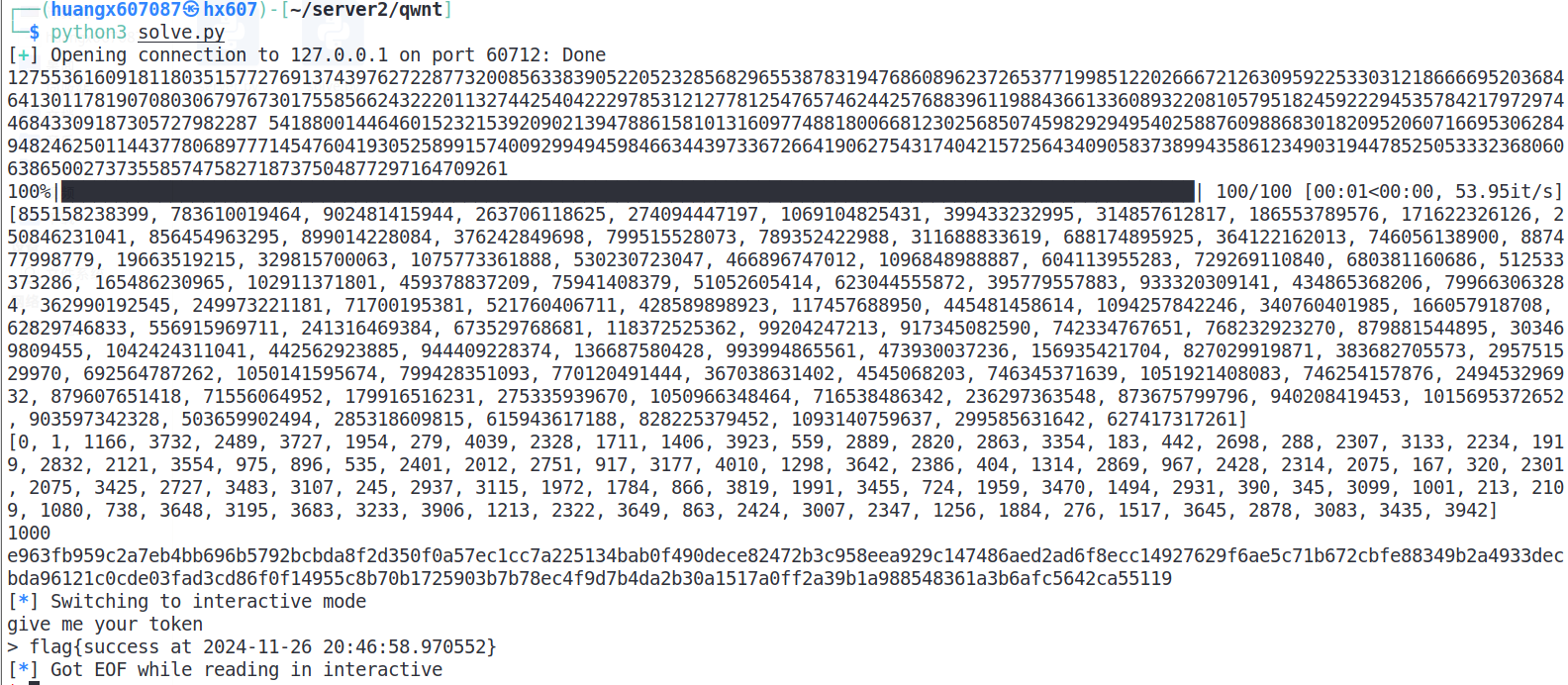
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
from pwn import *
from Crypto.Util.number import *
from tqdm import *
sh=remote('127.0.0.1',60712)
sh.recvuntil(b'n=')
n=sh.recvline(keepends=False)
n=sh.recvline(keepends=False)
n=eval(n)
t=sh.recvline(keepends=False)
t=sh.recvline(keepends=False)
t=eval(t)
print(n,t)

M=[]
T=[]
mask=(2**40-1)<<492
RATE2N=4096
POW2NE=pow(RATE2N,65537,n)%n

for i in trange(99+1):
	#print(len(M),len(T))
	sh.recvuntil(b'>')
	sh.send(hex(t)[2:].encode())
	msg=sh.recvline(keepends=False)
	middval=eval(msg)>>492
	M.append(middval)
	if(i==0):
		t=t*POW2NE%n
		continue
	prevmid=(M[-2]&0x000fffffffffffffffff)*RATE2N
	prevmid<<=492
	for j in range(RATE2N):
		y=prevmid-(j*n)
		y=y&mask
		y=y>>492
		if(abs(y-middval)<RATE2N):
			T.append(j)
			break
	t=t*POW2NE%n
print(M)
print(T)
RR2=0
for i in range(len(T)):
	RR2*=4096
	RR2+=T[i]
C=(RR2*n)>>(12*99)

print(C.bit_length())

ansstr='{:0250x}'.format(C+1)

print(ansstr)
sh.sendline(ansstr.encode())
sh.interactive()

测试结果图中，[0,1,1166,...,3942] 的数组表就表示的相除向下取整得到结果的从高位到低位的 $4096$ 进制的表示。不过最后解出来 $t$ 之后，经过测试，再加1才是正确答案。

3

2.[HITCTF2024]supercomputer

先看一眼题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def f(x):
    x ^= ((x >> 11) & 0xb114514bb114514b)
    x ^= ((x << 13) & 0x114514cc114514cc)
    x ^= ((x << 17) & 0xaa191981aa191981)
    x ^= ((x >> 19) & 0xb1919810b1919810)
    x ^= ((x << 23) & 0x114514cd114514cd)
    x ^= ((x >> 29) & 0xb114514ab114514a)
    x ^= ((x << 31) & 0x114514cb114514cb)
    x ^= ((x << 37) & 0xaa19198caa19198c)
    x ^= ((x >> 41) & 0xb191981db191981d)
    x ^= ((x << 43) & 0x114514ce114514ce)
    return x

def calc(n):
    x = 0x1122334455667788
    for _ in range(n):
        x = f(x)
    return x
assert calc(1) == 0xaa732acf4eb6a79d
assert calc(10) == 0x28262ecbd673b7d7
assert calc(100) == 0x23a6b8be477b7c3
assert calc(1000) == 0x93737600f66aa785
assert calc(100000) == 0x8a762387c4e3aed8
assert calc(1000000) == 0x1267270a756bf7df
assert calc(10000000) == 0x39377648f4e367d7
assert calc(100000000) == 0x82232f8777773e8a
assert calc(1000000000) == 0x8762b83d6faa783
assert calc(10000000000) == 0x27237cdd6726788
assert calc(100000000000) == 0x97f6b44e7fe66de
assert calc(1000000000000) == 0x88723b8666ff27ca
assert calc(10000000000000) == 0x8a32670ee5ef6ec0
assert calc(100000000000000) == 0x993b3b4265ea6edb
assert calc(1000000000000000) == 0x8b732ec065e7e795
print('flag{%s}' % hex(calc(10000000000000000)))

题目给出了一个 $64$ 比特的变换过程，并给出了 $10^{0}\sim10^{14}$ 次变换过程的结果，要求经过 $10^{15}$ 次比特变换的结果。

很明显，题目给出的数字很大，并且是比特变换，因此可以往矩阵快速幂的地方想。

然后十分钟不到，写好了这个函数，构造之后却不对。。然后一步一步地对着调试，发现只进行一步的时候是对的，进行两步就开始不对了。。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#Sagemath
def get(t,a,b):
    vec2k=[1<<i for i in range(64)]
    xornum=vec2k.copy()
    if(t==1):
        for i in range(64):
            xornum[i]>>=a
            #xornum[i]&=(2**64-1)
    if(t==-1):
        for i in range(64):
            xornum[i]<<=a
            xornum[i]&=((2**64)-1)
    
    mask=[int(bool(b&(1<<i))) for i in range(64)]
    xored=[mask[i]*xornum[i] for i in range(64)]
    result=[(vec2k[i]^^xored[i])&((2**64)-1) for i in range(64)]
    M=[[0 for _ in range(64)] for __ in range(64)]
    for i in range(64):
        for j in range(64):
            M[i][j]=((result[i]&(1<<j))!=0)
    return Matrix(GF(2),M)

然后调前两步的时候，发现先乘 $M_{13}$ 再乘 $M_{11}$ 可以得到正确结果。原来矩阵变换方式为 $(\prod M)\vec v=M_1M_2M_3\vec v$（还是以三个举例）。根据矩阵变换的几何意义，先跟 $\vec v$ 相乘的是 $M_3$，也就是正着乘，先进行了 $M_3$ 对应的变换。那就还是一个一个来，倒着乘。

那么答案就出来了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#sage
def get(t,a,b):
    vec2k=[1<<i for i in range(64)]
    xornum=vec2k.copy()
    if(t==1):
        for i in range(64):
            xornum[i]>>=a
            #xornum[i]&=(2**64-1)
    if(t==-1):
        for i in range(64):
            xornum[i]<<=a
            xornum[i]&=((2**64)-1)
    
    mask=[int(bool(b&(1<<i))) for i in range(64)]
    # print(mask)
    # print(xornum)
    xored=[mask[i]*xornum[i] for i in range(64)]
    # print(xored)
    result=[(vec2k[i]^^xored[i])&((2**64)-1) for i in range(64)]
    # print([ '{:016X}'.format(i) for i in result])
    M=[[0 for _ in range(64)] for __ in range(64)]
    for i in range(64):
        for j in range(64):
            M[i][j]=((result[i]&(1<<j))!=0)
    return Matrix(GF(2),M)

Marr=[]
Marr.append(get(-1,11,0xb114514bb114514b))
Marr.append(get(1,13,0x114514cc114514cc))
Marr.append(get(1,17,0xaa191981aa191981))
Marr.append(get(-1,19,0xb1919810b1919810))
Marr.append(get(1,23,0x114514cd114514cd))
Marr.append(get(-1,29,0xb114514ab114514a))
Marr.append(get(1,31,0x114514cb114514cb))
Marr.append(get(1,37,0xaa19198caa19198c))
Marr.append(get(-1,41,0xb191981db191981d))
Marr.append(get(1,43,0x114514ce114514ce))
Marr=Marr[::-1]
M=identity_matrix(GF(2),64)
for mi in Marr:
    M=M*mi
v0=[(0x1122334455667788&(1<<i))!=0 for i in range(64)]
v0=vector(v0)
v1=(M**10000000000000000)*v0
print(v1)
print('flag{%s}'%hex(vector(ZZ,[1<<i for i in range(64)])*(vector(ZZ,list(v1)))))
#(1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1)
#flag{0xa8276600c7e3b6d9}

3.[强网拟态2024]notiv

瞄一眼题目（注：题目非核心部分与原题略有改动，比如取消了proof_of_work，并改了一下flag的形式，但不影响题目原本难度和解题做法）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
# !/usr/bin/env python
from hashlib import sha256
import socketserver
import os
import sys
import random
import signal
import string
from hashlib import sha256
from mypad import *
from datetime import *
from Crypto.Cipher import AES
from random import *
from Crypto.Util.number import *


class Task(socketserver.BaseRequestHandler):
    def _recvall(self):
        BUFF_SIZE = 2048
        data = b''
        while True:
            part = self.request.recv(BUFF_SIZE)
            data += part
            if len(part) < BUFF_SIZE:
                break
        return data.strip()

    def send(self, msg, newline=True):
        try:
            if newline:
                msg += b'\n'
            self.request.sendall(msg)
        except:
            pass

    def recv(self, prompt=b'> '):
        self.send(prompt, newline=False)
        return self._recvall()

    def close(self):
        self.request.close()

    def handle(self):
        try:
            signal.alarm(120)
            count = 0
            for _ in range(50):
                seed(os.urandom(8))
                key = pad_x923(b"")
                print(key.hex())
                chal = hex(getrandbits(64*3))[2:].zfill(16*3)
                print(str(datetime.now()),chal)
                for i in range(200):
                    iv = long_to_bytes(getrandbits(128)).rjust(16, b"\00")
                    cipher = AES.new(key, AES.MODE_CBC, iv)
                    test = self.recv(b":> ").decode()
                    tb = bytes.fromhex(test)
                    ret = cipher.encrypt(pad_x923(tb))
                    if len(ret) > 16:
                        self.send(b"forbid")
                        continue
                    self.send((iv+ret).hex().encode())

                s = self.recv(b">> ").decode()
                print('s=',s)
                iv = bytes.fromhex(s[:32])
                print('iv=',iv)
                ans = bytes.fromhex(s[32:])
                print('ans=',ans)
                cipher = AES.new(key, AES.MODE_CBC, iv)
                att = cipher.decrypt(ans)
                print('attpad=',att)
                att = unpad_x923(att)
                print('att=',att,'chalEncode=',chal.encode())
                if att == chal.encode():
                    count += 1
            self.send(b"you got %d score" % count)
            if count >= 20:
                FLAG="flag{Success at "+str(datetime.now())+"}"
                FLAG=FLAG.replace(' ','-')
                self.send(b"cong!your flag is "+FLAG.encode())
            else:
                self.send(b"sorry,plz try again")
        except:
            self.send(b"something wrong! plz try again!")
            self.close()


class ThreadedServer(socketserver.ThreadingMixIn, socketserver.TCPServer):
    pass


class ForkedServer(socketserver.ForkingMixIn, socketserver.TCPServer):
    pass


if __name__ == "__main__":
    HOST, PORT = '127.0.0.1', 60717
    print(f'running on {HOST}:{PORT}')
    server = ForkedServer((HOST, PORT), Task)
    server.allow_reuse_address = True
    server.serve_forever()

其中：

1
2
3
4
5
from Crypto.Random import get_random_bytes

pad_x923=lambda x,block_size=16:x+get_random_bytes((block_size-(len(x)%block_size)-1))+bytes([(block_size-len(x)%block_size)])
unpad_x923=lambda x,block_size=16:x[:-((x[-1]-1)%block_size)-1]

注：get_random_bytyes 调用的是 os.urandom，不可预测。

题目拿到第一眼：getrandbits(128)，这妥妥的MT随机数预测，200次机会，说明156次就可以预测后面的随机数了。然后发现，题目要求是构造一个给定的 48 字节的串的密文（这个可以求出来，因为这个串是 getrandbits(64*3) 生成的，前向反推一次就行）。

但在题目中，每次只能对至多 15 字节内容进行加密，且加密填充方式为：填充 $n-1$ 个随机字符，然后再放入 1 字节填充长度来保证分组。当明文长度为 48 时，意味着密文长度为 64（因为要填充一整组）。且题目使用了 CBC 模式，也就是前一组密文和后一组明文异或后才是真正的加密内容，即：$IV=C_0$，$C_i=E(C_{i-1}\oplus M_i),i=1,2,3,4$。

经过分析后，我们可以大致地得到这些事实：

  1. 由于填充的随机性，因此，必须构造 15 字节的密文，这样才能保证 填充后字符串的确定性（只会填充一个\x01）
  2. 使用的IV是可以预测的，可以从这个地方出发考虑。
  3. 构造密文时，IV是可指定的，因此 $C_1$ 可以直接构造。同时，对 $C_4$ 的要求是：保证最后四个比特为 $0$ 就行，对应 $1/16$ 的概率。
  4. 因此本题重点是主要考虑 $C_2$ 和 $C_3$，且要保证能达到约 40 percent 的构造成功率。

设 $\mathrm{chal}=H_1,H_2,H_3,H_4$，其中可以假设 $H_4$ 为全零（根据第三条后半部分）。考虑直接构造：由于 $C_2=E_K(H_2\oplus C_1)$。而在之前选择明文的过程中：$C_2=E_K(M_2\oplus IV_2)$，因此，我们构造出来的 $M_2$ 应该为 $M_2=IV_2\oplus C_1\oplus H_2$。因此我们需要保证 $M_2$ 的最后一字节的十六进制为 $\mathtt{01H}$，这个概率为 $1/256$。

而同理，$M_3$ 也是 $1/256$ 的概率构造。那这样成功率算下来就是 $1/65536$，故期望得分为：
$$
E(\mathrm{Point})=\frac{50\times200}{65536}=0.1526
$$
也就是平均尝试六次，才只能得 $1$ 分。

借鉴的MaPl大哥的EXP，其中，mttool见本人博客中2021年7月的Explore MT19937文章。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
from pwn import *
from tqdm import *
from mttool import *

# 记录所有AES加解密对
AES_P, AES_C = [], []

def turn(sh, data: bytes):
	assert len(data) == 15
	sh.recvuntil(b':> ')
	sh.sendline(data.hex().encode())
	ret = sh.recvline().decode().strip()
	iv = bytes.fromhex(ret[:32])
	ciph = bytes.fromhex(ret[32:])
	AES_P.append(xor(data + b"\1", iv))
	AES_C.append(ciph)
	return iv, ciph

def getrandbits(F, bits):
	assert bits % 8 == 0
	state = [F.getstate() for _ in range(bits//32)][::-1]
	return b"".join(w.to_bytes(4, "big") for w in state)

def skip_state(F, state_count):
	for _ in range(state_count):
		F.getstate()

def xor(a, b):
    return bytes(a[i] ^ b[i] for i in range(min(len(a), len(b))))

sh = remote('127.0.0.1', 60717)

for i in range(50):
	AES_P, AES_C = [], []
	# 恢复随机数状态
	D = []
	F = MT19937()
	for _ in range(624//4):
		my_plain = b"0"*15 + b"\x01"
		iv, ciph = turn(sh, my_plain[:15])
		for j in [12, 8, 4, 0]:
			D.append(int.from_bytes(iv[j:j+4], 'big'))
	F.setstate(D)
	F.invtwist()
	F.invtwist()

	# 得到 chal
	skip_state(F, 624-6)
	chal = getrandbits(F, 24*8).hex().encode()
	print(f"chal: {chal}")
	P1 = chal[:16]
	P2 = chal[16:32]
	P3 = chal[32:]

	# 将随机数置为当前状态
	skip_state(F, 624)

	# 搜索加解密对，构造C2
	times = 200 - 624//4
	solve = []
	next_iv = getrandbits(F, 128)
	
	while times > 2:
		for P, C in zip(AES_P, AES_C):
			if (C[-1] ^ P2[-1] ^ next_iv[-1]) == 1:
				payload = xor(P2, next_iv)
				payload = xor(C, payload)
				assert payload[-1] == 1
				iv, ciph = turn(sh, payload[:15])
				assert iv == next_iv
				next_iv = getrandbits(F, 128)
				IV, C1, C2 = xor(P, P1), C, ciph
				if (C2[-1] ^ P3[-1] ^ next_iv[-1]) == 1: # 从已有结果构造 C3 (低概率)
					payload = xor(P3, next_iv)
					payload = xor(C2, payload)
					iv, ciph = turn(sh, payload[:15])
					assert iv == next_iv
					next_iv = getrandbits(F, 128)
					times -= 1
					C3 = ciph
					for P, C in zip(AES_P, AES_C): # 筛选出最后一组填充
						if (P[-1] ^ C3[-1]) % 16 == 0 and (C[-1] ^ next_iv[-1]) == 1:
							C4 = Cs
							print(f"[+] get solve:")
							print(f"\tIV: {IV.hex()}")
							print(f"\tC1: {C1.hex()}")
							print(f"\tC2: {C2.hex()}")
							print(f"\tC3: {C3.hex()}")
							print(f"\tC4: {C4.hex()}")
							solve.append((IV, C1, C2, C3, C4))
				break
		else:
			turn(sh, b"0"*15)
			next_iv = getrandbits(F, 128)
		times -= 1

	# context.log_level = "debug" 
	while times:
		turn(sh, b"0"*15)
		times -= 1

	sh.recvuntil(b'>> ')
	if solve:
		sh.sendline(b"".join(solve[0]).hex().encode())
	else:
		sh.send(b"00"*32)
print(sh.readline())

因为这个算法只求一个 $C_2$，然后对这个 $C_2$ 根据当前的IV去求 $C_3$，这样来的话概率当然会很低了。看了wp之后发现， wp的思路是存储所有满足条件的 $C_2$ 及其对应的 $C_1,IV$，然后对每个 $C_2$ 去用当前IV猜 $C_3$。由于一开始 $C_2$ 的数量少，因此如果没有找到合适的 $C_3$，则再获取一组可行的 $C_2$ 。

测了一下，一次运行大概可以获取 $19$ 个 $C_2$，尝试次数为 $19\times9=171$ 次。获取可行的 $C_3$ 的概率为 $1/256$，因此当获得 $19$ 个可行的 $C_2$ 后，就有很大的概率获取一个 $C_3$。

至于当前IV？IV是在获取 $156$ 组数据之后就可以预测出来，因此可以先进行测试，如果没有 $C_2$ 或者根据当前的 $C_2$ 找不到可行的 $C_3$，就可以再找一组 $C_2$。再本地进行枚举，找不到合适的就不交，不会浪费查询次数。

至于 $C_4$ ，可以认为 $H_4$ 为全 $0$，因此 $C_4$ 可以根据 $C_3$ 构造出来，概率为 $1/16$。

exp:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
from pwn import *
from tqdm import *
from Crypto.Util.number import *
from mttool import *

sh=remote('127.0.0.1',60717)
def sendMyMsg(msg):
	msghex=msg.hex()
	print(len(msghex),msghex)
	sh.recvuntil(b':> ')
	sh.sendline(msghex.encode())
	recvline=sh.recvline(keepends=False)
	recvline=recvline.strip()
	print(recvline)
	assert(len(recvline)==64)
	iv,ciph=recvline[:32],recvline[32:]
	iv,ciph=int(iv,16),int(ciph,16)
	plain=iv^ciph
	state4=[]
	iv00=iv
	for i in range(4):
		state4.append(iv&0xffffffff)
		iv>>=32
	return plain,ciph,state4,iv00
from tqdm import *
for o in tqdm(range(50)):
	V,M,C,D=[],[],[],[]#IV,realencmsg,cipher,32bitdata(iv)
	for i in range(156): #获取156组数据，624个state预测后续数值
		recvline=sendMyMsg(bytes([0]*15))
		M.append(recvline[0])
		C.append(recvline[1])
		D=D+recvline[2]
		V.append(recvline[3])
	F=MT19937()
	F.setstate(D)
	F.invtwist()
	F.invtwist()
	Ha=[F.getstate() for _ in range(624)]
	Ha=Ha[-6:]
	H=sum([Ha[i]<<(32*i) for i in range(6)]) #获取chal
	H=(hex(H)[2:].zfill(48))
	print(H)
	H1,H2,H3=[bytes_to_long(H[16*i:16*i+16].encode()) for i in range(3)]
	F.setstate(D)
	Fv=[sum([F.getstate()<<(32*_) for _ in range(4)]) for __ in range(44)] #获取后续IV
	V=V+Fv
	assert len(V)==200
	C0,C1,C2,C3,C4=0,0,0,0,0 #C0就是IV
	possC2=[]
	possC1ind=[]
	T=156
	while(T<200):
		print(possC2)
		ivT=V[T]
		foundC3=0
		for i in range(len(possC2)):#根据已有的 C2 去找 C3,如果找到了，就结束这一部分了
			X=ivT^possC2[i]^H3
			if(X%256==1): #只有构造出来的X满足末字节是01才可以
				msgX=(hex(X)[2:]).zfill(32)
				msgX=(hex(X)[2:]).zfill(32)
				msgX=bytes.fromhex(msgX) #如果明文X符合条件，就找发过去，获取这组C3并准备结束
				print(msgX)
				print('C3')
				recvline=sendMyMsg(msgX[:-1])
				T+=1
				C3=recvline[1]
				C2=possC2[i]
				C1=C[possC1ind[i]]
				C0=V[possC1ind[i]]^H1^1
				foundC3=1
				break
		if(foundC3): #找到C3立刻退出这个循环
			break
        #如果没有找到C3，那就寻找对应的 C2
		foundC2=0
		for i in range(len(C)):
			X=ivT^C[i]^H2 #通过所有的C[i]，构造可能的C2，这边的C[i]会被用作C1，因为C1构造很简单。
			if(X%256==1):
				msgX=(hex(X)[2:]).zfill(32)
				msgX=bytes.fromhex(msgX)
				print(msgX)
				recvline=sendMyMsg(msgX[:-1]) #如果明文X符合条件，就找发过去，获取这组C2
				T+=1
				possC2.append(recvline[1])
				C.append(recvline[1])
				possC1ind.append(i)
				foundC2=1
				break
		if(foundC2): #找到C2就看下一组数据
			continue
		else:
			recvline=sendMyMsg(bytes([0]*15)) #找不到C2，就再发一组00000...001过去凑数
			T+=1
			M.append(recvline[0])
			C.append(recvline[1])
	if(C0*C1*C2*C3):#如果C0,C1,C2,C3都找到了，就通过H4(H4=0) 去构造C4
		while(T<200):
			X=V[T]^C3^0 #这个异或H4=0可以不写，但为了明显起见，还是写出来
			if(X%16==1):
				X^=(X&0xf0)
				msgX='{:032X}'.format(X)
				msgX=bytes.fromhex(msgX)
				assert len(msgX)==16
				recvline=sendMyMsg(msgX[:-1])
				C4=recvline[1]
				T+=1
				break
			else:
				T+=1
				recvline=sendMyMsg(msgX[:-1])
				M.append(recvline[0])
				C.append(recvline[1])
		while(T<200):
			T+=1
			recvline=sendMyMsg(msgX[:-1])
			M.append(recvline[0])
			C.append(recvline[1])
		s=''
		for i in [C0,C1,C2,C3,C4]:
			s+='{:032X}'.format(i)
		print(s)
		sh.sendline(s.encode())
	else:#如果没有找到符合条件的数据，也要把次数用完，然后发一组全0跳掉这组数据。
		while(T<200):
			T+=1
			recvline=sendMyMsg(msgX[:-1])
			M.append(recvline[0])
			C.append(recvline[1])
		sh.sendline(bytes([48]*96))
sh.interactive()

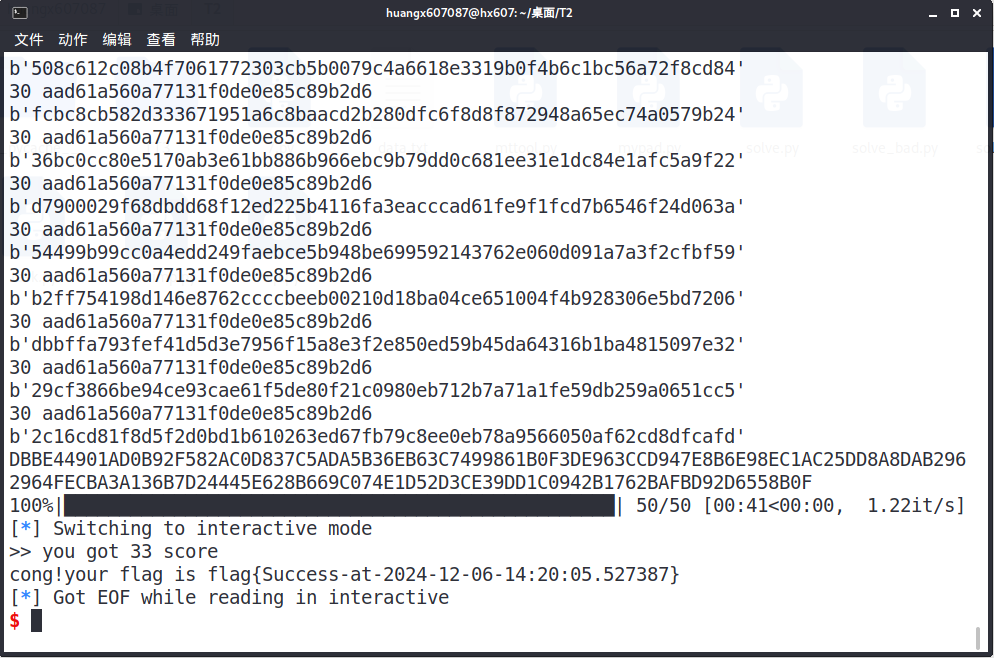
运行结果，最后运行时间为 $41$ 秒，符合题目两分钟的限时。

4

9.总结

没有总结，感觉自己水平还是不太够。。并且，12月期末周了，要做的东西好多，看看自己能不能平衡好吧。。。

CTFSeason4
#ExpLog
24Nov4
http://example.com/2024/12/06/24Nov4/
作者
huangx607087
发布于
2024年12月6日
许可协议