25Jan1
huangx607087 1月的切题1(NTRU Note 1)
0.Introduction
自从从贵州回来之后,就持续红温了45天,又是课程论文又是pre的,做了3个ppt,3个课程论文,5场考试,中途打了个CISCN。两门背诵的课搞了我15天,对我这种背书不行的家伙来说真的很难顶。。。
1 月 9 日11:00,终于考完了,反正能过。不得不说 12 月 5 号的密码学考试,不仅全是本科的知识,还比我本科密码学考得东西简单多了,大作业 5 个模块(AES,DES,MD5,SHA1,RSA),我本科全通过自定义代码写过,封装个GUI,三天光速完成,最后直接毫无压力地规格化 94 拿下它!
CTF,启动!竞赛,启动!
1.[2024强网杯决赛]fak1
1x01 题目大意
一个NTRU题目,先看眼题目:
1 | |
其中:
1 | |
1x02 题目分析
先回顾一下NTRU加密过程:产生私钥 $f(x)\in T(d_f,d_f-1)$,其中 $T(d_1,d_2)$ 表示具有 $d_1$ 个系数为 $1$,$d_2$ 个系数为 $-1$ 的多项式集合。然后计算 $f_p(x)=R_p\left(\dfrac{1}{f(x)}\right)$, $f_q(x)=R_q\left(\dfrac{1}{f(x)}\right)$。在此基础上,随机产生仅含系数 $0,1$ 的多项式 $g(x)\in R_q$。私钥为 $f(x),f_p(x),f_q(x),g(x)$,公钥为 $h(x)=pg(x)f_q(x)\in R_q$。加密方式为随机产生小系数多项式 $r(x)$,计算 $c(x)=h(x)r(x)+m(x)$
这里,是给出了 10 次机会,每次让你选择一个 $m(x)$,然后会给出 $c_i(x)=h(x)r_i(x)+s(x)+m_i(x)$ 。其中:$h(x),c(x)$ 已知,$m_i(x)$ 自行构造。那么我们可以有 $\bar c_i(x)=c_i(x)-m_i(x)=h(x)r_i(x)+s(x)$。
处理之后,由于 $r(x)$ 仅包含 $0,1$,可以计算 $d_i(x)=\bar c_0(x)-\bar c_i(x),x=1,2,…,9$,来消除 $s(x)$。再计算 $\bar d_i(x)=\dfrac{d_i(x)}{h(x)}$,就可以得到两个 $r_0(x)-r_i(x)$ 的差了,如果某个系数是 $1$,则说明 $r_0(x)$ 对应系数为 $1$;如果某个系数是 $-1$,则说明 $r_0(x)$ 对应的系数为 $0$;如果为 $0$,说明无法确定这个情况。但 $9$ 组数据,基本够用了。。。
1x03 exp
不是很难,但NTRU以前自己没见过,确实不太好搞。
1 | |
可能的运行结果:
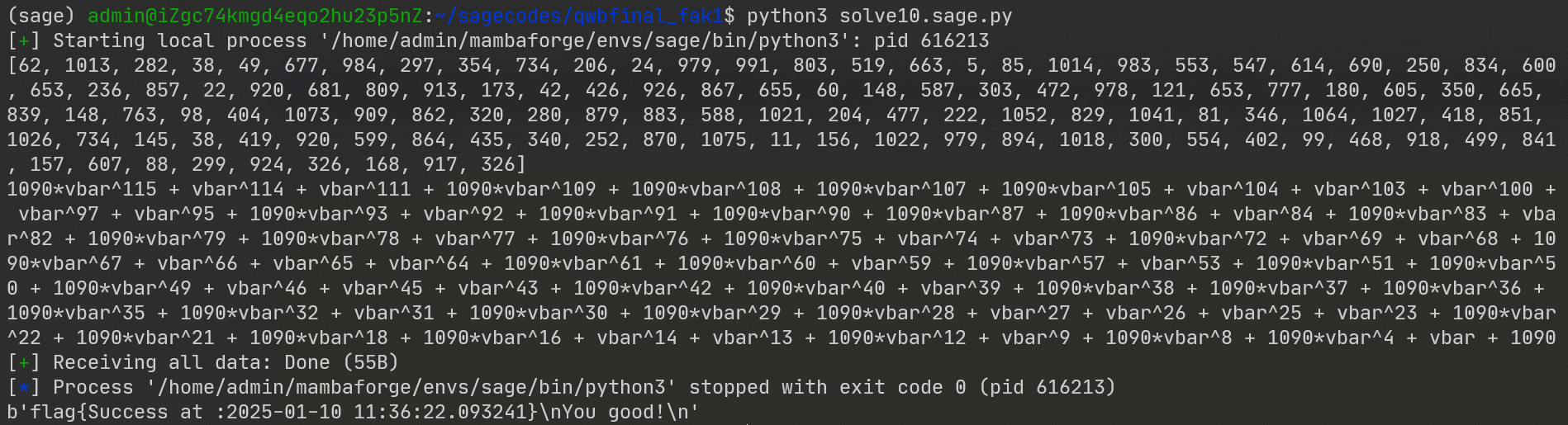
2.[2024强网杯决赛]f2ke
2x01 题目大意
老规矩,还是先看一看题目:
1 | |
这个和上一题的区别,就在于:每一次的公钥 $h(x)$ 都产生了变化,并且交互次数达到了 $60$ 次。乍一看,感觉是NTRU的广播攻击,但感觉次数不太够。(确实不太够,要 $176$ 次交互)
2x02 NTRU的广播攻击学习
2x02.1 modulus=$x^n-1$
不过,自己这个时候还不太会NTRU的广播攻击,于是,先学一下NTRU的广播攻击。在原始NTRU中,使用的取模多项式是 $x^n-1$,但题目是 $x^n+1$,因此先看 $x^n-1$ 的情况:
当模数为 $x^n-1$ 时,对应的公钥 $h(x)$ 的系数矩阵为一个循环矩阵,类似于这样的形式,该矩阵大概率可逆:
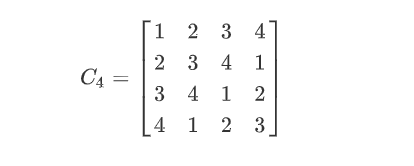
因此,NTRU写成矩阵的形式就是:
$$
H\vec r+\vec m=\vec c
$$
由于矩阵 $H$ 大概率可逆,那么可以有:
$$
\vec r+H^{-1}\vec m=H^{-1}\vec c
$$
设 $H^{-1}=K,H^{-1}\vec c=\vec b$,那么这个式子变成:
$$
\vec r+K\vec m=\vec b
$$
移项,有
$$
\vec r=\vec b-K\vec m
$$
两边平方:
$$
\vec r^2=\vec b^2-2\vec b\cdot(K\vec m)+(K\vec m)^2
$$
如果我们已知 $\vec r^2$,那么,可以有:
$$
\vec r^2-\vec b^2=(K\vec m)^2-2\vec b\cdot(K\vec m)
$$
写得规范一点,就是:
$$
\vec r^2-\vec b^2=\vec m^TK^TK\vec m-2\left(\vec b^TK\right)\vec m
$$
设:
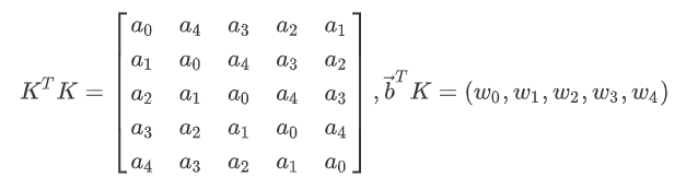
可以得到:
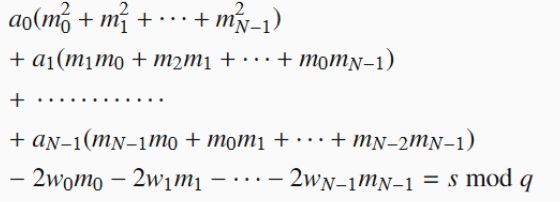
其中 $s=\vec r^2-\vec b^2$,这里 $\vec r^2$ 已知。由于 $\vec r$ 仅含 $0,1,-1$,那么 $\vec r^2$ 就是 $\vec r$ 中非零分量的个数,那么最终结果为
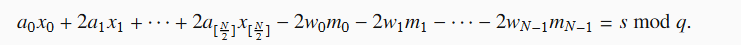
因此,这里有 $n+\left\lceil\dfrac{n}{2}\right\rceil$ 个未知数,我们只需要构造对应数量的方程,就可以去解方程了!
不过自己根据论文代码实现时,发现总有点小问题,矩阵不满秩,导致最后结果总是会偏移 $x^{n-1}$ 的系数。反正那个值就是 $0,±1$,特判一下就行。
Code:
1 | |
可能的输出结果(很显然,解出来的结果有 $-2$,说明整体偏移了一个 $ -1$,直接调回来就行):
1 | |
2x02.2题目参数
在搞懂基本原理后,我们回到题目的参数,由于模数变成了 $x^n+1$,并且, $\vec r$ 为完全随机的 $0,1$ 向量。
既然模数改变了,那么之前的矩阵也会有所变化,需要重新设为:
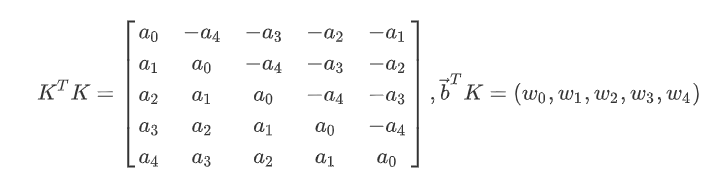
由于刚才是 $\vec r=\vec b-K\vec m$,这里可以两边乘 $2$,再减去一个全 $1$ 向量,变为:
$$
2\vec r-\vec 1=2(\vec b-K\vec m)-\vec 1
$$
由于 $\vec r$ 仅含 $0,1$,那么 $2\vec r-\vec 1$ 就仅含 $-1,1$ 了,两边平方有:
$$
(2\vec r-\vec 1)^2=4(\vec b-K\vec m)^2-4(\vec b-K\vec m)\cdot \vec 1+\vec 1^2
$$
由于 $(2\vec r-\vec 1)^2=\vec 1^2=n$,这两个可以直接约掉,然后进行系数化简:
$$
0=(\vec b-K\vec m)^2-(\vec b-K\vec m)\cdot \vec 1
$$
继续处理一下:
$$
\vec b^2-\vec b\cdot \vec 1=2\vec b^TK\vec m-\vec m^TK^TK\vec m-(K\vec m)\cdot \vec 1
$$
左边的都是已知量,很好算,然后我们看看右边三项的表达式:
第一项给所有的 $m_i$ 项带来了一个 $w_i$;第三项给每个 $ m_i$ 又带来了一个 $K$ 的第 $i$ 列系数之和,即 $m_i$ 的系数为$\sum_j K^{T}_{ij}$
而第二项也出现了一点点小变化:我们来测试一下,发现此时有 $x_i=-x_{n-i}$。
1 | |
然后再考察一下 $K^TK$,测试发现,有 $a_i=-a_{n-i}$
那么: $a_ix_i+a_{n-i}x_{n-i}$,照样等于 $2a_ix_i$。那么可以不对原来的ntru.sage文件做任何改变。
1 | |
可能的运行结果,可以看出,这个不一定总能正常运行,因为矩阵 $H$ 的逆矩阵 $H^{-1}$ 并非总存在。

2x03 简化版本:400次询问
因此,如果原题给出 400 次询问,那么就可以使用广播攻击方式去做(其实176次就够了,这里搞成400次,主要是因为一开始懒得算次数了,实际也只用了176组数据)
1 | |
可能的运行结果:
2x04 原题做法
原题的话,只有60次询问机会,次数还是不太够。
然后在2010-598那篇论文中,我看到了这样一句话:
如果 $ES$ 只有 $0,1$ 两种取值,那么我们可以增加 $n$ 个方程: $r_i^2-r_i=0$。
在 $\vec r=\vec b-K\vec m$ 中,我们考察 $\vec r$ 的每一个分量所涉及到的关系,以三个为例:
$$
r_0=b_0-\vec K_0\vec m=b_0-(K_{00}m_0+K_{01}m_1+K_{02}m_2)
$$
两边变换,有:
$$
r_0^2-r_0=\left(b_0-(K_{00}m_0+K_{01}m_1+K_{02}m_2)\right)^2-(b_0-(K_{00}m_0+K_{01}m_1+K_{02}m_2))
$$
等号左边显然为 $0$,对等号右边展开:
1 | |
等号一遍留下 $b_0^2-b_0$,那么右边就是这一堆玩意:
1 | |
整理一下:
一次项: $m_0$ 系数为 $-2K_{00}b_0+K_{00}$,$m_1$ 系数为 $-2K_{01}b_0+K_{01}$,$m_2$ 系数为 $-2K_{02}b_0+K_{02}$
平方项: $m_0^2$ 系数为 $-K_{00}^2$,同理,$m_1^2,m_2^2$ 的系数分别为 $-K_{01}^2,-K_{02}^2$ 。
交叉项: $m_im_j$ 系数为 $-2K_{0i}K_{0j}$。
那么,我们就有了 $n$ 个一次项,$n$ 个平方项,$\dfrac{n(n-1)}{2}$ 个交叉项,一共 $\dfrac{n(n+3)}{2}$ 个未知数,一次广播攻击可以取得 $n$ 个未知数。
然后,原题是 $117$,最后的矩阵规模高达 $7020\times7020$,光是跑这个构造就要耗我一小时,在服务器上跑快一点,但2核2G的服务器,直接炸掉了。。。。
不过,为了测试正确性,还是得做一下的。。。。因此,我把 $n$ 从 $117$ 调成了 $47$,$d_f,d_g$ 从 $(35,37)$ 调为 $(7,7)$,仅用于测试正确性,因此,最后的交互次数也从 $60$ 下降到了 $25$。
1 | |
运行结果:

原题的数据就不测了,两边设备条件都不是很允许我测。。。。根据 $O(n^3)$ 的复杂度看,目测要跑一天!
3.fake2的非预期做法—NTRU子环攻击
3x01 分析
其实我一开始就发现,这里用 $117$ 作为指数,就不太对。很明显,$117=3^2\times13$ ,不是一个素数。又看到是广播攻击,因此也许可能能CRT?
我们可以注意到:
$$
x^3+1=(x+1)(x^2-x+1)
$$
那么,$x^{117}+1$ 也可以被分解成:
$$
x^{117}+1=(x^{39}+1)(x^{78}-x^{39}+1)
$$
然后题目的交互次数是 $60$ 次,对于 $x^{39}+1$ 的模数,貌似刚好够打(59次)。但对于 $x^{78}-x^{39}+1$ 呢?
不过据说可以直接对公钥开打,构造NTRU矩阵,其中 $H$ 的第 $i$ 行表示 $x^ih(x)$ 的列表表示,请注意,$i$ 从 $0$ 开始。
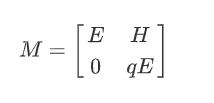
对这个 $M$ 进行 BKZ ,最后有可能得到 $(f,3g)$ 的值(因为题目是 $h(x)=pg(x)r(x),p=3$)。不过这个 $f$ 可能会出现 $2$,因为是在子环上打的。因此,可以对 60 组公钥分别开打,寻找一个合适的公钥,使其在 $R_{q,78}$ 和 $R_{q,39}$ 上都能得到很小的值。60次机会,貌似还是够用的。
3x02 实验测试
然后就是实验测试:
1 | |
可能的输出结果
1 | |
为了方便调试,我对原题进行了修改,令其每次生成的私钥 $f(x)$ 会被写入一个文件中去。我打开这个文件,找到了第 $50$ 组私钥
1 | |
然后测一下:
1 | |
你会发现,$y$ 并不是仅包含 $0,1,-1$,还包含了很多其他的值。因为我们BKZ出来的是得到循环移位的东西。
测一下:
1 | |
也就是,在 $R_{q,78}$ 中,$\dfrac{y(x)}{f(x)}=x^{23}$,在 $R_{q,39}$ 中,$\dfrac{y(x)}{f(x)}=x^{25}$。看来可以爆破?还真是。
1 | |
但,在实际做题的时候,我们并不知道私钥,因此需要加一个判断测试一下:
1 | |
这个输出结果是有规律的,最后解出来的东西也是私钥的循环移位。不过貌似不是每次都能解出来的,因为 $x^{39}+1$ 的分解太多了,很容易出现不可逆的结果。
多调试了几次,拿到了一组结果,随机取最后一组结果
1 | |
然后调试了一下:
1 | |
然后发现第一组也可以,看来私钥的移位不影响最后解密结果。那干脆直接找到一组break掉就ok了。
3x03 exp
1 | |
可能的运行结果,也是概率成功。在本地跑,70秒时间似乎是够的。
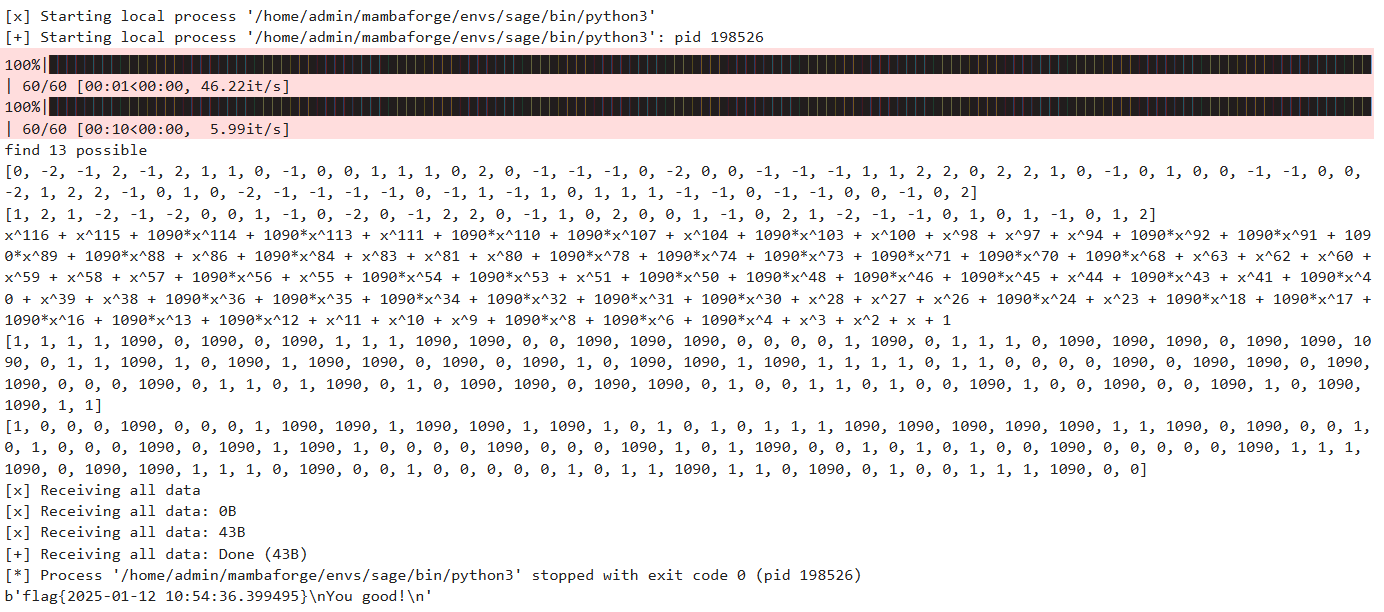
9.总结
两个NTRU题目,知识又增长了,好耶!
不过后面还有一堆题目要补,继续加油!