ECCNotes4

huangx607087学习ECC的笔记4

最近更新时间：2025.2.8 16:00，第 5 次更新

Reference:鸡块佬的blog，awda的blog

0.About

BlockCipher3：2021.09.04，BlockCiphser4：2024.11.06，中间38个月

LatticeNotes7：2021.07.25，LatticeNotes8：2024.12.05，中间41个月

然后，ECCNotes，经过47个月，也要更新了。。。回顾了以下之前写的，满头问号：我之前写了啥？还好，看了2h，看懂了。。。

ECCNotes 发布时间 主要内容
$1$ $2021.02.21$ 椭圆曲线基本知识
$2$ $2021.03.04$ 椭圆曲线的双线性对(1)
$3$ $2021.03.25$ 椭圆曲线上的除式、广播攻击和相关明文攻击
$4$ $2025.02.01$ 椭圆曲线上的同源，SIDH

究其原因，是因为之前0xGame2024 Week4出了个SIDH，当时完全看不懂，那边wp写得也挺简陋的。并且感觉最近多项式、同态这些玩意在CTF中出现得越来越多（盲猜dbt佬读博研究方向的就是多项式啥的，然后出了好多多项式的题）。

特别提醒：本文内容均为 “测代码测出来” 的，没有给复杂的证明，因为复杂度证明我自己都看不懂。。。SIDH和CSIDH的论文我其实都看了一下，但有些知识真的很晦涩难懂。。因此最终还是选择使用测代码的方式来给出结论。

那么今天这个就以SIDH入手介绍同源吧，先给个0xGame2024 Week4的题目代码，后面就围绕着这个代码了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
from random import randint
from secret import flag

ea, eb = 110, 67
p = 2**ea*3**eb - 1
F.<i> = GF(p**2, modulus=[1,0,1])

E0 = EllipticCurve(F, [1,0])

PA = E0.random_point()
QA = E0.random_point()
sA = randint(0, 2**ea)
RA = PA + sA*QA
print(f'RA = {RA.xy()}')

RB_= [int(i) for i in input(f'[+] Give me RB:\n>').split(',')]
#Example: 1,2,3,4 

RB = E0(RB_[0]*i + RB_[1], RB_[2]*i + RB_[3])
phi_B =  E0.isogeny(RB, algorithm='factored')
E_B = phi_B.codomain()
assert E_B.is_isogenous(E0)

R_share = phi_B(PA) + sA * phi_B(QA)
phi_share = E_B.isogeny(R_share, algorithm='factored')
secret = phi_share.codomain().j_invariant()

secret_ = [int(i) for i in input('[+] Tell me the secret\n>').split(',')]
secret_ = secret_[0] * i + secret_[1]
# #Example: 1,2

if secret_ == secret:
 	print(f'[+] flag:{flag}')
else:
 	print('[+] Wrong')

1. SIDH预备知识

1.1 超奇异曲线

超奇异曲线：若模 $p$ 下的椭圆曲线 $E$ 的阶满足 $\mathrm{ord}(E)\equiv 1\pmod p$ ，则 $E$ 是超奇异曲线

1
2
3
4
5
6
7
8
p=71
C71.<img>=GF(71**2,modulus=[1,0,1])
E1=EllipticCurve(C71,[7,2])
E2=EllipticCurve(C71,[11,9])
print(E1.order() % p , E1.is_supersingular(),E1.j_invariant())
#1 True 66
print(E2.order() % p , E2.is_supersingular(),E2.j_invariant())
#62 False 30

1.2 j-不变量

1.2.1 j-不变量的定义

如果 2 个曲线 $E_1$ 和 $E_2$ 具有相同的 j-不变量，则两条曲线同构。

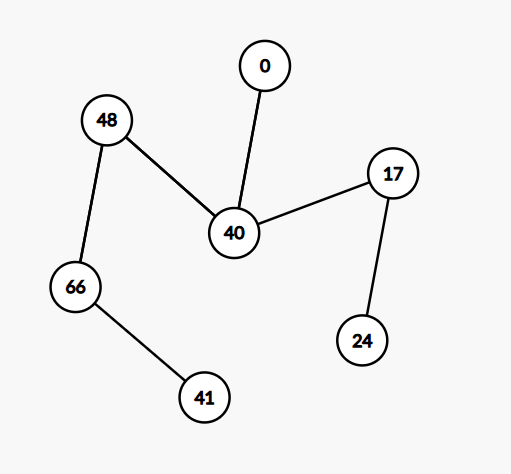
设 $\mathbb C_{71}=\mathbb Z_{71}+\mathrm i\mathbb Z_{71}$ ，其中 $\mathrm i^2\equiv -1\pmod{71}$，则定义在 $\mathbb C_{71}$ 上的超奇异曲线有 以下 $7$ 个j-不变量，或者说，若 $\mathbb C_{71}$ 上某个椭圆曲线的j-不变量为下面的数值中的某个，则这条曲线是超奇异曲线。

1
[0, 17, 24, 40, 41, 48, 66]

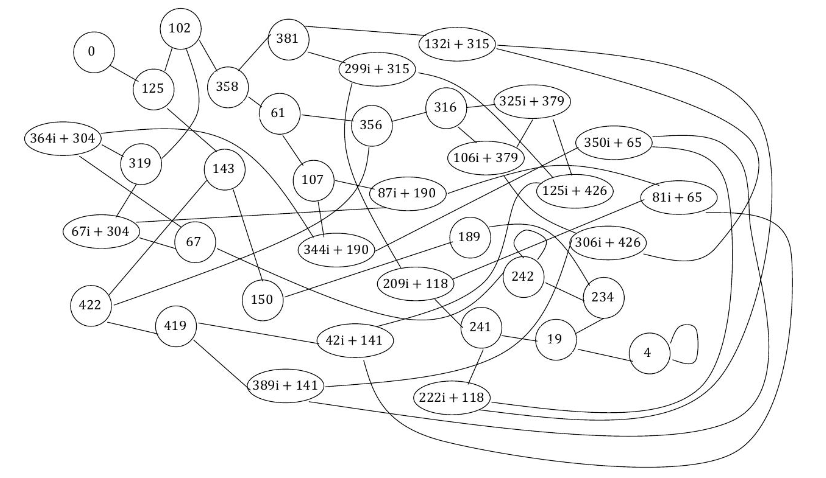
如果 $p=431$，则对应的超奇异曲线上会有 $37$ 个 j-不变量，如下所示：

1
[0, 4, 19, 61, 67, 102, 107, 125, 143, 150, 189, 234, 241, 242, 316, 319, 356, 358, 381, 419, 422, 81*img + 65, 350*img + 65, 209*img + 118, 222*img + 118, 42*img + 141, 389*img + 141, 87*img + 190, 344*img + 190, 67*img + 304, 364*img + 304, 132*img + 315, 299*img + 315, 106*img + 379, 325*img + 379, 125*img + 426, 306*img + 426]

扩展到任意 $p$，则 j-不变量的个数为 $\left\lfloor\dfrac{p}{12}\right\rfloor+z$ 个，其中 $z$ 的取值为 $0,1,2$，与 $p$ 的值有关。

1.2.2 j-不变量与同构

我们设： $E_1:y^2\equiv x^3+7x+2\pmod{71}$ 和 $E_2:y^2\equiv x^3+11x+52\pmod {71}$ 的 j-不变量均为 $66$，因此这两条曲线均为 $\mathbb C_{71}$ 上的超奇异曲线，且满足同构性质，同构表达式为：
$$
\phi:E_1(x,y)\rightarrow E_2(23x,20\mathrm iy)
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
p=71
C71.<img>=GF(71**2,modulus=[1,0,1])
E1=EllipticCurve(C71,[7,2])
E2=EllipticCurve(C71,[11,52])
f = E1.torsion_polynomial(1).monic()
phi=EllipticCurveIsogeny(E1,f,E2)
phi.rational_maps()
#(23*x, (20*img)*y)
k=randint(1,p)
G=E1.random_element()
G2=G*k
x,y=G.xy()
x,y=23*x,20*img*y
H=E2(x,y)
H2=H*k
H2.x()/G2.x(),H2.y()/G2.y()
#23 20*img

再举一个 $\mathbb C_{431}$ 上的例子，两条曲线分别为 $E_1:y^2=x^3+(208\mathrm i+161)x^2+x$ 和 $E_2:y^2=x^3+(172\mathrm i+162)x^2+x$，其映射为：
$$
\phi:E_1(x,y)\rightarrow E_2(\left(\left(66 \mathrm{i} + 182\right) x + 300 \mathrm{i} + 109, \left(122 \mathrm{i} + 159\right) y\right)
)
$$

1
2
3
4
5
6
7
8
9
from random import *
p=431
C431.<img>=GF(p**2,modulus=[1,0,1])
E1=EllipticCurve(C431,[0,208*img+161,0,1,0])
E2=EllipticCurve(C431,[0,172*img+162,0,1,0])
f = E1.torsion_polynomial(1).monic()
phi=EllipticCurveIsogeny(E1,f,E2)
phi.rational_maps()
#((66*img + 182)*x + (-131*img + 109), (122*img + 159)*y)

当然adwa告诉我有更简单的办法：

1
2
3
4
5
6
7
8
p=71
C71.<img>=GF(71**2,modulus=[1,0,1])
E1=EllipticCurve(C71,[7,2])
E2=EllipticCurve(C71,[11,52])
phi=E1.isomorphism_to(E2)
print(phi.rational_maps())
#(23*x, (20*img)*y)

1.3 蒙哥马利曲线

之前我们在密码学中常用的曲线形式为 $y^2=x^3+ax+b$，但其实椭圆曲线的完整表达形式为 $y^2+a_1xy+a_3y=x^3+a_2x^2+a_4x+a_6$。而蒙哥马利曲线的表达式为 $y^2=x^3+ux^2+x$。

感谢@adwa 的指正，之前一个版本误写成了 $x^3+ux+x$

注意这里 $x$ 的系数为 $1$，而新增加的 $x^2$ 的系数可以变动，和之前的曲线相比，可以发现 $(0,0)$ 一定在蒙哥马利曲线上。

对于蒙哥马利曲线而言，其 j-不变量可以快速计算为 $j(Em)=\dfrac{256(u^2-3)^3}{u^2-4}$。对于两个j-不变量相同的蒙哥马利曲线，它们之间的同态映射中表达式中不会出现分母。（1.2.2的两个例子）。

当然，常用曲线和蒙哥马利曲线之间的交集为 $y^2=x^3+x$，这对应的是 $u=0,b=0$ 的情况，该曲线也多用于SIDH中。当然，任意形式的椭圆曲线都可以转化为与其j-不变量相同的蒙哥马利曲线形式，在Sagemath中，可以调用 E.montgomery_model() 实现。在1.9.4中的代码中，可以验证这一性质。

为了简化问题，我们定义曲线 $E$ 的蒙哥马利参数为 $E$ 的蒙哥马利形式中年的 $u$ 值，Sage中可以使用 E.montgomery_model().a2() 实现。

1.4 同源

1.4.1 倍点同构映射

刚才我们其实已经接触到了同源的概念，但我们以”同构”去描述的（呃，因为信安数基中讲的是同构），但事实上，同构是同源的特殊情况。在之前的同构映射中，也可以使用一个看似trivial的方法，自己跟自己的二倍点映射：

1
2
3
4
5
6
7
8
9
10
11
12
13
from random import *
p=71
Cp.<img>=GF(p**2,modulus=[1,0,1])
E=EllipticCurve(Cp,[1,0])
print(E._multiple_x_numerator(2))
print(E._multiple_x_denominator(2))
#x^4 + 69*x^2 + 1
#4*x^3 + 4*x
phi = E.scalar_multiplication(2)
print(phi.rational_maps()[0])
print(phi.rational_maps()[1])
#(x^4 - 2*x^2 + 1)/(4*x^3 + 4*x)
#(8*x^6*y - 31*x^4*y + 31*x^2*y - 8*y)/(-7*x^6 - 14*x^4 - 7*x^2)

这里的映射结果为：

$$
\phi:(x,y)\rightarrow\left(\frac{x^{4} + 69 x^{2} + 1}{4 x^{3} + 4 x}, \frac{8 x^{6} y + 40 x^{4} y + 31 x^{2} y + 63 y}{64 x^{6} + 57 x^{4} + 64 x^{2}}\right)
$$

如果我们令 $x$ 的分母 $4x^3+4x=0$，也就是 $x^3+x=0$，那么可以得到 $x=0,\mathrm i,-\mathrm i$。可以利用 division_points 去实现，相当于有限域开 $n$ 次根。

1
2
3
L=(E(0).division_points(2))
print(L)
#[(0 : 1 : 0), (0 : 0 : 1), (img : 0 : 1), (70*img : 0 : 1)]

由于 $E$ 的阶为 $72$，那么也一定存在阶为 $3$ 的情况（显然，如果 $P$ 的阶为 $3$，那么 $-P$ 的阶也是 $3$），那么也存在某个点和自己的三倍点映射：

1
2
3
4
5
print(E._multiple_x_denominator(3).monic())
#x^8 + 4*x^6 + 27*x^4 + 46*x^2 + 8
L=(E(0).division_points(3))
print(L)
#[(0 : 1 : 0), (2 : 9 : 1), (2 : 62 : 1), (69 : 9*img : 1), (69 : 62*img : 1), (19*img : 15*img + 56 : 1), (19*img : 56*img + 15 : 1), (52*img : 15*img + 15 : 1), (52*img : 56*img + 56 : 1)]

解方程 $x^8 + 4x^6 + 27x^4 + 46x^2 + 8=0$，可以得到对应的解为 $±\sqrt{±\frac{1}{2} \sqrt{±2 \sqrt{497} - 42} - 1}$，这个解在 $\mathbb C_{71}$ 中就变成了 $2,69,19\mathrm i,52\mathrm i$，此时的映射表达式如下（已经开始复杂了！）
$$
\phi:(x,y)\rightarrow\left(\frac{x^{9} + 59 x^{7} + 30 x^{5} + 36 x^{3} + 9 x}{9 x^{8} + 36 x^{6} + 30 x^{4} + 59 x^{2} + 1}
,\frac{18 x^{12} y + 41 x^{10} y + 12 x^{8} y + 48 x^{6} y + 7 x^{4} y + 13 x^{2} y + 17 y}{60 x^{12} + 5 x^{10} + 21 x^{8} + 27 x^{6} + 64 x^{4} + 40 x^{2} + 53}
\right)
$$
对于阶为 $l$ 的点，也就是满足 $lP=\mathcal O$ 的点构成的集合，我们可以叫做 $l$-torsion。也可以把这个集合记为 $\ker(l)$，有 $\ker(l)$ 与 $\mathbb Z_{l+1}^2$ 同构。若 $l$ 为素数，则可以构成 $l+1$ 个阶为 $l$ 的循环子群，且两个不同子群之间的元素是线性无关的。

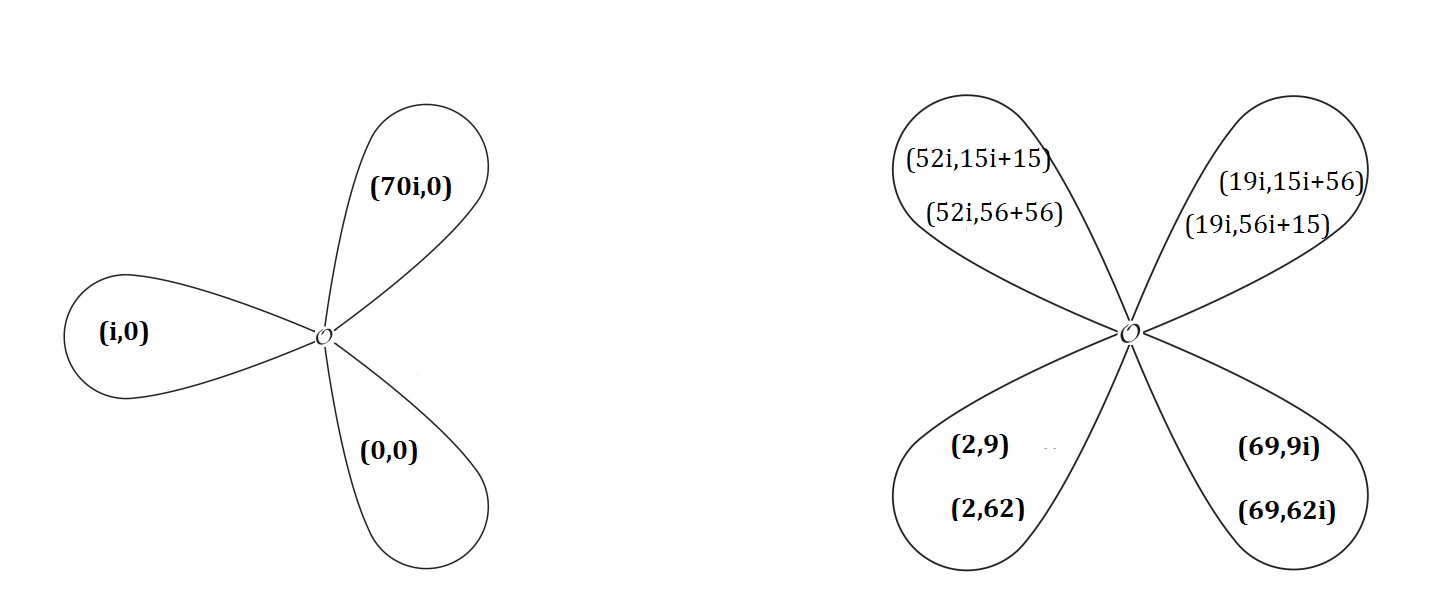
$\ker(2)$ 和 $\ker(3)$ 的结构如下图所示，中间是无穷远点 $\mathcal O$。这个花瓣形的结构，貌似在之前导师发给我的双线性对那个PPT上见过。

1

1.4.2 同源在Sage中的实现

可以使用Sage来实现同源，这里选择了 $(69,9\mathrm i)$ 作为同源映射，可以看到， $E_1$ 的 j-不变量为 $24$，而 $E_2$ 的 j-不变量为 $66$。说明 $E_2$ 与 $E_1$ 并不是同构的。而我们刚才说过，同源的一种特殊情况是同构，同构是只有一个核元素 $\mathcal O$ 的同源，因此这里只有 $E_1$ 和 $E_2$ 同源，没有 $E_1$ 和 $E_2$ 同构。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from random import *
p=71
Cp.<img>=GF(p**2,modulus=[1,0,1])
E1=EllipticCurve(Cp,[1,0])
print(E1.j_invariant())
#24
A = E1(69,9*img)
phi = E1.isogeny(A)
#Isogeny of degree 3 from Elliptic Curve defined by y^2 = x^3 + x over Finite Field in img of size 71^2 to Elliptic Curve defined by y^2 = x^3 + 13*x + 5 over Finite Field in img of size 71^2
E2 = phi.codomain()
print(E2)
print(E2.j_invariant())
print(phi.rational_maps()[0])
print(phi.rational_maps()[1])
#Elliptic Curve defined by y^2 = x^3 + 13*x + 5 over Finite Field in img of size 71^2
#66
#(x^3 + 4*x^2 + 30*x + 12)/(x^2 + 4*x + 4)
#(x^3*y + 6*x^2*y - 14*x*y - 35*y)/(x^3 + 6*x^2 + 12*x + 8)

1.4.3 同源图

如果我们把 $\mathbb C_{71}$ 上的 $7$ 个 超奇异 j-不变量各构造一条曲线，并取每条曲线上 $\ker (2)$ 中的三个点（不包括 $\mathcal O$）进行同源，可以得到这样的一个图。在这边，按理说每个点的度都应该是 $3$，但由于存在自环和重边，当然也有特殊情况，因此只有一个点的度是 $3$。比如 $40$ 连接的三条边，说明 j-不变量为 $40$ 的曲线中， $\ker(2)$ 中的三个非无穷远点经过同源，得到的新的同源曲线的 j-不变量可能是 $48,0,17$。

当然，可以发现，这是一个无向图，因为同源是对偶的，也就是说，j-不变量为 $40$ 的曲线可以同源到 j-不变量为 $48$ 的曲线，反过来，也存在 j-不变量为 $48$ 的曲线同源到 j-不变量为 $40$ 的曲线上去。而对于一条路径 $40\rightarrow48\rightarrow 66$ 而言，这相当于两次度为 $2$ 的的同源，也可以视为一次 度为 $4$ 的同源。

2

这个是 $p=431$ 的 $\ker(2)$ 同源图，由于这里的j-不变量有 $73$ 个，因此度为 $3$ 的点占了大多数。当然，也可以选择 $\ker(3)$ 进行度为 $3 $ 的同源，那么每个点的度就是 $4$ 了，得到的图也会与 $\ker(2)$ 得到的图不一样。

3

1.9 总结和回顾

1.9.1 Sage求j不变量的方法

1
2
3
4
Fp2.<img>=GF(431**2,modulus=[1,0,1])
E=EllipticCurve(Fp2,[26,48+33*img])
E.j_invariant()
#51*img + 353

1.9.2 判断一个曲线是不是超奇异曲线

超奇异曲线的定义：对于定义在 $\mathbb F_{p^k}$ 上的曲线$E$ ，满足 $|E|\equiv 1 \pmod p$ 的曲线，也就是每个点的阶除以 $p$ 的余数均为 $1$ 的曲线。

判断方法：E.is_supersingular()

CryptoHack上的例题：在一堆 $A$ 中找到满足超奇异椭圆曲线的 $A$。

1
2
3
4
5
6
7
8
p=71
C71.<img>=GF(71**2,modulus=[1,0,1])
E1=EllipticCurve(C71,[7,2])
E2=EllipticCurve(C71,[11,9])
print(E1.is_supersingular(),E1.j_invariant())
#True 66
print(E2.is_supersingular(),E2.j_invariant())
#False 30

1.9.3 同源的性质

由于同源性不仅是曲线之间的有理映射，而且还是保留这些曲线上的群结构的映射。因此，即使 $\phi:E\rightarrow E’$ 未知，如果我们已经知道了 $E’$ 上的两个点 $\phi(P),\phi(Q)$，仍然可以高效地计算 $\phi(P+Q)=\phi(P)+\phi(Q)$ 和 $\phi(kP)=k\phi(P)$。

假设我们知道 $p=62207$，$\phi(P)=(6369\mathrm i+10044,1511\mathrm i+60746),\phi(Q)=(35306\mathrm i+34293,7667\mathrm i+35815)$，那么我们可以直接解出曲线 $E’:y^2=x^3+ax+b$ 的参数 $a,b$，随后直接计算 $\phi(P+Q)=\phi(P)+\phi(Q)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
p=2**8*3**5-1
Cp.<img>=GF((p,2),modulus=[1,0,1])
Px,Py=(Cp([10044,6369]),Cp([60746,1511]))
Qx,Qy=(Cp([34293,35306]),Cp([35815,7667]))
M=Matrix(Cp,[[Px,1],[Qx,1]])
y=vector(Cp,[Py**2-Px**3,Qy**2-Qx**3])
print(M.solve_right(y))
#(4664*img + 27806, 309*img + 49495)
E=EllipticCurve(Cp,(4664*img + 27806, 309*img + 49495))
G=E(Px,Py)
H=E(Qx,Qy)
print((G+H).xy())
#(59811*img + 19477, 25623*img + 59043)

1.9.4 求一个曲线的蒙哥马利曲线形式

1
2
3
4
5
6
7
8
9
10
E=EllipticCurve(GF(419),[33,9])
E.montgomery_model()
print(E.montgomery_model())
print(E.montgomery_model().a2())
print(E.j_invariant())
print(E.montgomery_model().j_invariant())
#Elliptic Curve defined by y^2 = x^3 + 173*x^2 + x over Finite Field of size 419
#173
#272
#272

1.9.5 同源上的离散对数问题

由于同源中所用的模数 $p$ 满足 $p-1$ 光滑或 $p+1$ 光滑，因此可以在这里解离散对数，来看这样一个题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
from Crypto.Util.number import *
from random import *
from secret import flag
p=2**110*3**67-1
F.<img>=GF((p,2), modulus=[1,0,1])
E=EllipticCurve(F, [1,0])
P,Q = E.gens()
a,b,c,d=1,1,1,1
while(1):
    a,b=getPrime(p.nbits()-1),getPrime(p.nbits()-1)
    if(isPrime(a*b+2)):
        pab=a*b+2
        break
while(1):
    c,d=getPrime(p.nbits()-1),getPrime(p.nbits()-1)
    if(isPrime(c*d+2)):
        pcd=c*d+2
        break
n=pab*pcd
m=bytes_to_long(flag)
enc=pow(m,998244353,n)
print(f'{n=}')
print(f'{enc=}')
print(f'{P=}')
print(f'{Q=}')
print(f'{a*P+b*Q=}')
print(f'{c*P+d*Q=}')
#n=85339866424199254883523559880615666512135381522585732793528431470377062744274254649973052920620568928504698841752053780787873200084113130883908840908212945037412690974720035898852421861507580011712163085069539142027604357576603852989568568703518497258863875153
#enc=53196193209459904075636522116569983302576854763250689338898932442142670012786364854411445956198339404091802217781375861501894434580028683650559746806106285471896793278331422155924857505573872814397852509320854345311674565845751058899294650766501770021007913380
#P=(48078665342759973922737682036708423814190721092041844128027005717*img + 101453330026777115174150344369057670486666592516047972012938796665 : 106414280972661281085621154931449660232878796703063973273414757742*img + 39724328357561096793476627099678863783547841068613222678288745599 : 1)
#Q=(93500514099794038270009024277832755039609701103181802675798729052*img + 47897193222031858455386507623256296001957037047526619598509235406 : 54198645028294833136677496634472064101831735083974811027732624298*img + 75625331732228140758389762066194385021895005176305694866704994925 : 1)
#a*P+b*Q=(99438327946055727177889400304218359448668814328993888248956295877*img + 4968626040861611178418787464521937488397920200577632479183463224 : 105950216810563991098390220256849202423207554566800612407368235975*img + 3691834310963900683221595180172998514255729221504935470233846876 : 1)
#c*P+d*Q=(51107307256620573344750692242449535834731290150105231422519471003*img + 93155460640102509761079363280109781081212723193482509556965830289 : 55648112626812914269722588029837092719545646171682298767546807156*img + 76607528540202433402606873074289417539785602790560632206527541013 : 1)

方法1

很明显，我们要求出 $a,b,c,d$ 的值，才能够解出flag。但这个椭圆曲线上的生成元有两个，因此直接调用离散对数是不太现实的，可以利用同源，比如 phi1=E.isogeny(P) 后，有 $\phi_1(P)-\mathcal O$，相当于同源之后，新的曲线 $E_1$ 上的点经过 $\phi_1$，实现了对 $P$ 进行了”取模”操作。

不过sagemath似乎直接调用会报错，考虑到阶是光滑的，偷一个PoligHellman的代码，改一下就OK了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
def PoligHellman(G,Y,order):
    factors, exponents = zip(*factor(order))
    temp=[]
    for i in range(len(factors)):
        q=factors[i]
        a=[]
        for j in range(1,exponents[i]+1):
            GG=G*(order//q**j)
            YY=Y*(order//q**j)
            for k in range(q):
                s=0
                for t in range(len(a)):
                    s+=a[t]*q^t
                s+=k*q^(len(a))
                if s*GG==YY:
                    a.append(k)
                    break
        x_q=0
        for j in range(len(a)):
            x_q+=a[j]*q^j
        temp.append(x_q)
    f=[]
    for i in range(len(factors)):
        f.append(factors[i]**exponents[i])
    return crt(temp,f)
phi1,phi2=E.isogeny(P,algorithm='factored'),E.isogeny(Q,algorithm='factored')
E1,E2=phi1.codomain(),phi2.codomain()
#discrete_log(phi2(R),phi2(P)) #Error.
a=PoligHellman(phi2(P),phi2(G),p+1)
b=PoligHellman(phi1(Q),phi1(G),p+1)
c=PoligHellman(phi2(P),phi2(H),p+1)
d=PoligHellman(phi1(Q),phi1(H),p+1)
print(a,b,c,d)
assert(a*P+b*Q==G and c*P+d*Q==H)
pab=a*b+2
pcd=c*d+2
phi=(pab-1)*(pcd-1)
n=85339866424199254883523559880615666512135381522585732793528431470377062744274254649973052920620568928504698841752053780787873200084113130883908840908212945037412690974720035898852421861507580011712163085069539142027604357576603852989568568703518497258863875153
enc=53196193209459904075636522116569983302576854763250689338898932442142670012786364854411445956198339404091802217781375861501894434580028683650559746806106285471896793278331422155924857505573872814397852509320854345311674565845751058899294650766501770021007913380

assert n==pab*pcd
from Crypto.Util.number import *
d=inverse(998244353,phi)
print(long_to_bytes(pow(enc,d,n)))
#a=104387901776481921020491968026212561265236729786055540819430222523 
#b=103077386564589714869729922397059093530581882186115640326801660297 
#c=82858008941957494629539360515452860058651023741867958937507591339 
#d=95720266381793956333967392421282383472307483512312215027077560801
#b'flag{781f9d8c-d318-4e31-9416-bec6e2cfa016}'

update：这么做也可以，但必须指定 operation='+'

1
discrete_log(phi1(G),phi1(Q),operation='+')
方法2

当然，也可以使用双线性对的知识，由于 $G=aP+bQ$，可以使用weil_pairing求解，得到：
$$
e(G,Q)=e(aP+bQ,Q)=e(aP,Q)e(bQ,Q)=e(P,Q)^a
$$
同理：
$$
e(P,G)=e(P,aP+bQ)=e(P,aP)e(P,bQ)=e(P,Q)^b
$$
这样 $a,b$ 就可以通过离散对数解出来了，同理解得 $c,d$，这样就不需要用同源的知识了！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from Crypto.Util.number import *
from random import *
p=2**110*3**67-1
F.<img>=GF((p,2), modulus=[1,0,1])
E=EllipticCurve(F, [1,0])
P=E(48078665342759973922737682036708423814190721092041844128027005717*img + 101453330026777115174150344369057670486666592516047972012938796665,
 106414280972661281085621154931449660232878796703063973273414757742*img + 39724328357561096793476627099678863783547841068613222678288745599)
Q=E(93500514099794038270009024277832755039609701103181802675798729052*img + 47897193222031858455386507623256296001957037047526619598509235406,
 54198645028294833136677496634472064101831735083974811027732624298*img + 75625331732228140758389762066194385021895005176305694866704994925)
G=E(99438327946055727177889400304218359448668814328993888248956295877*img + 4968626040861611178418787464521937488397920200577632479183463224,
 105950216810563991098390220256849202423207554566800612407368235975*img + 3691834310963900683221595180172998514255729221504935470233846876)
H=E(51107307256620573344750692242449535834731290150105231422519471003*img + 93155460640102509761079363280109781081212723193482509556965830289,
 55648112626812914269722588029837092719545646171682298767546807156*img + 76607528540202433402606873074289417539785602790560632206527541013)
def ee(X,Y):
    return X.weil_pairing(Y,p+1)
a=discrete_log(ee(G,Q),ee(P,Q))
b=discrete_log(ee(P,G),ee(P,Q))
c=discrete_log(ee(H,Q),ee(P,Q))
d=discrete_log(ee(P,H),ee(P,Q))
print(a,b,c,d)
assert(a*P+b*Q==G and c*P+d*Q==H)
#104387901776481921020491968026212561265236729786055540819430222523 
#103077386564589714869729922397059093530581882186115640326801660297 
#82858008941957494629539360515452860058651023741867958937507591339 
#95720266381793956333967392421282383472307483512312215027077560801

2.SIDH算法

2.1 算法流程

在上面的基础知识下，我们开始介绍 SIDH 算法

1.双方选择模数 $p=2^\alpha3^\beta k-1$，其中尽量使 $2^{\alpha}≈3^{\beta}$，$k$ 通常取 $1$。和一条 $\mathbb C_{p}$ 上的超奇异椭圆曲线（一般为 $y^2=x^3+x$）。此处我们选择 $p=71=2^{3}3^{2}-1$ ，$E:y^2=x^3+x$ 在 $\mathbb C_{p}$ 上的 j-不变量为 $24$。

1
2
3
4
5
from random import *
ea,eb=3,2
p=2**ea*3**eb-1
Cp.<img>=GF(p**2,modulus=[1,0,1])
E=EllipticCurve(Cp,[1,0])

2.A选择 $E$ 上阶为 $2^\alpha$ 的两个线性无关的点 $P_A,Q_A$ （可以发现 $E$ 上有两个阶为 $72$ 的生成元，因此相对来说还是比较容易取到的），同理，B选择 $E$ 上阶为 $3^\beta$ 的两个线性无关的点 $P_B,Q_B$。判断 $P,Q$ 线性无关的方法，就是双线性对 $e(P,Q)$ 的值不为 $1$，也就是 $Q$ 无法写成 $kP$ 的形式。双方分别公开 $P_A,Q_A,P_B,Q_B$ 作为公共参数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from random import *
def genA(Ec):
    while(1):
        Pa=Ec.random_element()*((p+1)//2**ea)
        if(Pa!=E(0) and Pa.order()==2**ea):
            break
    while(1):
        Qa=Ec.random_element()*((p+1)//2**ea)
        if(Qa.weil_pairing(Pa,2**ea)!=1 and Qa.order()==2**ea):
            break
    return Pa,Qa
def genB(Ec):
    while(1):
        Pb=Ec.random_element()*((p+1)//3**eb)
        if(Pb!=E(0) and Pb.order()==3**eb):
            break
    while(1):
        Qb=Ec.random_element()*((p+1)//3**eb)
        if(Qb.weil_pairing(Pb,3**eb)!=1 and Qb.order()==3**eb):
            break
    return Pb,Qb
Pa,Qa=genA(E)
Pb,Qb=genB(E)
print(Pa.xy(),Qa.xy(),Pa.weil_pairing(Qa,2**ea))
print(Pb.xy(),Qb.xy(),Pb.weil_pairing(Qb,3**eb))
#(20*img + 13, 24*img + 45) (53*img + 32, 46*img + 7) 6*img + 65
#(36*img + 68, 15*img + 12) (62*img + 27, 21*img + 10) 29*img + 56

3.A随机选择秘密值 $x_A$，计算 $S_A=P_A+x_AQ_A$。然后计算同源 $\phi_A:E\rightarrow E_A$，其中 $\phi_A$ 为 $\alpha-1$ 个 $2$ 次同源组合而成，最终结果与 $S_A$ 相关。因此，我们得到 A 的公钥为 $E_A,\phi_A(P_B),\phi_A(Q_B)$，私钥为 $x_A,S_A$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
xa=randint(2,2**ea-1)
Sa=Pa+xa*Qa
print(xa,Sa.xy())
Sa1=Sa
E1=E
Pas,Eas=[],[E]
for i in range(ea-1,0,-1):
    Ta=Sa1*(2**i)
    phi = E1.isogeny(Ta)
    Eai = phi.codomain()
    Sa1 = phi(Sa1)
    E1=Eai
    Pas.append(phi)
    Eas.append(Eai)
phiA=Pas[-1]
for i in range(len(Pas)-2,-1,-1):
    phiA*=Pas[i]
print(phiA)
for i in range(len(Eas)):
    print(Eas[i].j_invariant(),end='  ->  ' if i!=len(Eas)-1 else '\n')
"""
Output:
6 (20*img + 58, 45*img + 24)
Composite morphism of degree 4 = 2^2:
  From: Elliptic Curve defined by y^2 = x^3 + x over Finite Field in img of size 71^2
  To:   Elliptic Curve defined by y^2 = x^3 + 27*x + 41 over Finite Field in img of size 71^2
24  ->  24  ->  17
"""

4.同理，B随机选择秘密值 $x_B$，计算 $S_B=P_B+x_BQ_B$。然后计算同源 $\phi_B:E\rightarrow E_B$，其中 $\phi_B$ 为 $\beta-1$个 $3$ 次同源组合而成，最终结果与 $S_B$ 相关。因此，我们得到 B 的公钥为 $E_B,\phi_B(P_A),\phi_B(Q_A)$，私钥为 $x_B,S_B$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
xb=randint(2,3**eb-1)
Sb=Pb+xb*Qb
print(xb,Sb.xy())
Sb1=Sb
E1=E
Pbs,Ebs=[],[E]
for i in range(eb-1,0,-1):
    Tb=Sb1*(3**i)
    phi = E1.isogeny(Tb)
    Ebi = phi.codomain()
    Sb1 = phi(Sb1)
    E1=Ebi
    Pbs.append(phi)
    Ebs.append(Ebi)
phiB=Pbs[-1]
for i in range(len(Pbs)-2,-1,-1):
    phiB*=Pbs[i]
print(phiB)
for i in range(len(Ebs)):
    print(Ebs[i].j_invariant(),end='  ->  ' if i!=len(Ebs)-1 else '\n')
"""
6 (54, 18)
Isogeny of degree 3 from Elliptic Curve defined by y^2 = x^3 + x over Finite Field in img of size 71^2 to Elliptic Curve defined by y^2 = x^3 + 13*x + 66 over Finite Field in img of size 71^2
24  ->  66
"""

5.此时，双方的公钥如下，并且在上面的输出中，我们可以看到，A 共存储了 $\alpha=3$ 条曲线，这三条曲线的j-不变量分别为：$24,24,17$，B存储了 $\beta=2$ 条曲线，其 j-不变量分别为 $24,66$。（双方第一个 $24$ 为原始曲线）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
PKA=(phiA.codomain(),phiA(Pb),phiA(Qb))
PKB=(phiB.codomain(),phiB(Pa),phiB(Qa))
print(PKA)
print(PKB)
"""
PKA:
(Elliptic Curve defined by y^2 = x^3 + 27*x + 41 over Finite Field in img of size 71^2, 
(19*img + 2 : 37*img + 67 : 1), 
(57*img + 11 : 4*img + 51 : 1))
PKB:
(Elliptic Curve defined by y^2 = x^3 + 13*x + 66 over Finite Field in img of size 71^2, 
(23*img + 44 : 32*img + 7 : 1), 
(46*img + 50 : 22*img + 43 : 1))
"""

6.在完成上述的步骤后，A使用B的公钥 $E_B,\phi_B(P_A),\phi_B(Q_A)$ 和自己的私钥 $x_A$，计算 $S_{AB}=\phi_B(P_A)+x_A\phi_B(Q_A)$，然后走和之前相同的步骤。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Eab=phiB.codomain()
Pab,Qab=phiB(Pa),phiB(Qa)
Sab=Pab+xa*Qab
print(Sab.xy())
Sab1=Sab
Eab1=Eab
Pabs,Eabs=[],[Eab]

for i in range(ea-1,0,-1):
    Tab=Sab1*(2**i)
    phi = Eab1.isogeny(Tab)
    Eabi = phi.codomain()
    Sab1 = phi(Sab1)
    Eab1=Eabi
    Pabs.append(phi)
    Eabs.append(Eabi)
phiAB=Pabs[-1]
for i in range(len(Pabs)-2,-1,-1):
    phiAB*=Pabs[i]
print(phiAB)
for i in range(len(Eabs)):
    print(Eabs[i].j_invariant(),end='  ->  ' if i!=len(Eabs)-1 else '\n')
"""
Output:
(26*img + 40, 3*img + 35)
Composite morphism of degree 4 = 2^2:
  From: Elliptic Curve defined by y^2 = x^3 + 13*x + 66 over Finite Field in img of size 71^2
  To:   Elliptic Curve defined by y^2 = x^3 + 14*x + 56 over Finite Field in img of size 71^2
66  ->  48  ->  40
"""

7.同理，B使用A的公钥 $E_A,\phi_A(P_B),\phi_A(Q_B)$ 和自己的私钥 $x_B$，计算 $S_{BA}=\phi_A(P_B)+x_B\phi_A(Q_B)$，然后走和之前相同的步骤。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
Eba=phiA.codomain()
Pba,Qba=phiA(Pb),phiA(Qb)
Sba=Pba+xb*Qba
print(Sba.xy())
Sba1=Sba
Eba1=Eba
Pbas,Ebas=[],[Eba]

for i in range(eb-1,0,-1):
    Tba=Sba1*(3**i)
    phi = Eba1.isogeny(Tba)
    Ebai = phi.codomain()
    Sba1 = phi(Sba1)
    Eba1=Ebai
    Pbas.append(phi)
    Ebas.append(Ebai)
phiBA=Pbas[-1]
for i in range(len(Pbas)-2,-1,-1):
    phiBA*=Pbas[i]
print(phiBA)
for i in range(len(Ebas)):
    print(Ebas[i].j_invariant(),end='  ->  ' if i!=len(Ebas)-1 else '\n')
"""
Output:
(23, 7)
Isogeny of degree 3 from Elliptic Curve defined by y^2 = x^3 + 27*x + 41 over Finite Field in img of size 71^2 to Elliptic Curve defined by y^2 = x^3 + 14*x + 56 over Finite Field in img of size 71^2
17  ->  40
"""

8.最终，A在计算时，得到的曲线的j-不变量的变化过程为：$66,48,40$，而B得到的曲线的j-不变量变化过程为 $17,40$。因此，双方共享的秘密值为 $40$。

2.2 代码实现

重构一下前面的代码：

2.2.1 Init

1
2
3
4
5
from random import *
alph,beta=8,5
p=2**alph*3**beta-1
Cp.<img>=GF(p**2,modulus=[1,0,1])
E=EllipticCurve(Cp,[1,0])

2.2.2 ParamGen

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def paramGen(Ec,K,eK,e5K):
    assert K in [2,3]
    P=Ec(0)
    J=5-K
    while(K**(eK-1)*P==Ec(0)):
        P=(J**e5K)*Ec.random_element()
    Q=Ec(0)
    while(P.weil_pairing(Q,K**eK)**(K**(eK-1))==1):
        Q=(J**e5K)*Ec.random_element()
    return P,Q

        
Pa,Qa=paramGen(E,2,alph,beta)
print('Pa =',Pa.xy())
print('Qa =',Qa.xy())
Pb,Qb=paramGen(E,3,beta,alph)
print('Pb =',Pb.xy())
print('Qb =',Qb.xy())
"""
Pa = (39380*i + 3466, 17196*i + 12226)
Qa = (16683*i + 35698, 11691*i + 44683)
Pb = (32011*i + 53204, 48668*i + 25851)
Qb = (3742*i + 40029, 60467*i + 51431)
"""

2.2.3 KeyGen

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def pkGen(P,Q,Po,Qo,x,Ec):
    S = P+x*Q
    phi =  Ec.isogeny(S,algorithm="factored")
    E1 = phi.codomain()
    return E1,phi(Po),phi(Qo)
xa=randint(2,2**alph-1)
xb=randint(2,3**beta-1)
print('xa =',xa)
print('xb =',xb)
Ea,Ga,Ha = pkGen(Pa,Qa,Pb,Qb,xa,E)
Eb,Gb,Hb = pkGen(Pb,Qb,Pa,Qa,xb,E)
print(f'Ea : {Ea}')
print(f'Ga = {Ga.xy()}\nHa = {Ha.xy()}')
print(f'Eb : {Eb}')
print(f'Gb = {Gb.xy()}\nHb = {Hb.xy()}')
"""
xa = 72
xb = 174
Ea : Elliptic Curve defined by y^2 = x^3 + (10061*i+1875)*x + (44734*i+35632) over Finite Field in i of size 62207^2
Ga = (2283*i + 47170, 34825*i + 48025)
Ha = (40463*i + 37692, 51159*i + 38421)
Eb : Elliptic Curve defined by y^2 = x^3 + (49242*i+18182)*x + (7897*i+49589) over Finite Field in i of size 62207^2
Gb = (27311*i + 57671, 21378*i + 7288)
Hb = (31852*i + 50453, 6044*i + 46259)
"""

2.2.4 + Key Exchange

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def getSecret(Ec,P,Q,x):
    Key = P+x*Q
    phi =  Ec.isogeny(Key,algorithm="factored")
    return phi.codomain().j_invariant()

Keya = getSecret(Eb,Gb,Hb,xa)
print('Keya =',Keya)
Keyb = getSecret(Ea,Ga,Ha,xb)
print('Keyb =',Keyb)
assert Keya==Keyb
"""
Keya = 10325*i + 49607
Keyb = 10325*i + 49607
Assert Pass.
"""

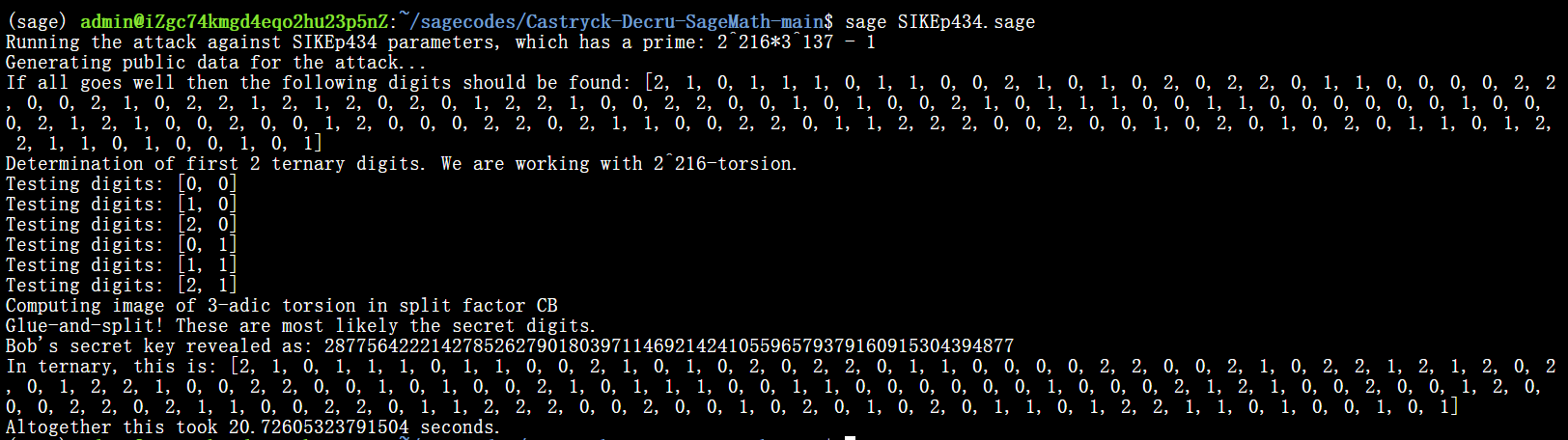
2.3 SIDH安全性分析

2.3.1 论文链接 & 论文附着代码

SIDH目前已经被破解了，GitHub上目前也有了很多SageMath的的代码，A 可以在只知道 B 的公钥的情况下，确定 B 的私钥。最快的方法只需要几十秒就可以攻破 400 位标准的参数。

论文链接2022-975
攻击SIDH的代码

论文中代码的运行结果：

5

2.3.2 06010型曲线的攻击

当然作为一个CTFer，既然人家都已经破解了SIDH了，我们当然要学会用他的代码。

可以看到，该代码中，使用的是 $y^2=x^3+6x^2+x$ 的曲线，而CTF题目中，常用的曲线是 $y^2=x^3+x$，很明显，两个曲线都是蒙哥马利曲线，但不同源，所以不存在同构映射。

在阅读论文之后，可以发现，论文的核心部分，是要构造出一个曲线上的自同态 $\phi$，满足 $\phi(\phi(P))=-4P$。这个 $\phi$ 又被记作 $\phi_{2\mathrm i}$。可以发现，这个攻击代码中的 public_values_aux.py 文件中，有这样一个函数，似乎限制死了曲线的形式为 $y^2=x^3+6x^2+x$。

1
2
3
4
def generate_distortion_map(E):
    if E.a_invariants() != (0,6,0,1,0):
        raise NotImplementedError
    return E.isogeny(E.lift_x(ZZ(1)), codomain=E)

而阅读其攻击代码SIKEp434.sage，可以发现这样一行，恰好是为了求 $\phi_{2\mathrm i}$ 用的

1
two_i = generate_distortion_map(E_start)

经过测试也的确如此：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def generate_distortion_map(E):
    if E.a_invariants() != (0,6,0,1,0):
        raise NotImplementedError
    return E.isogeny(E.lift_x(1), codomain=E)
p=2**8*3**5-1
F.<i>=GF((p,2),modulus=[1,0,1])
E1=EllipticCurve(F,[0,6,0,1,0])
G=E1.random_element()
phi=generate_distortion_map(E1)
print(G.xy())
print((-4*G).xy())
print(phi(phi(G)).xy())
(54868*i + 58756, 51614*i + 43751)
(32804*i + 60579, 20634*i + 8371)
(32804*i + 60579, 20634*i + 8371)

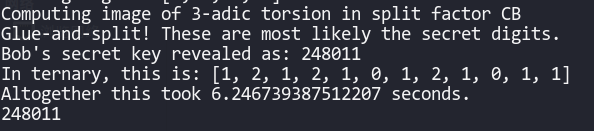
因此，只要我们搞出了 $\phi_{2\mathrm i}$，那么我们就可以直接使用其代码了。我们可以先从Git上下载这个代码的zip，解压到某个文件夹中，然后写入这样的测试代码（答案是 $248011$）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import public_values_aux
from public_values_aux import *

load('castryck_decru_shortcut.sage')

a, b = 18,13

p = 2^a*3^b - 1 # do not change

public_values_aux.p = p
Fp2.<i> = GF(p^2, modulus=x^2+1)
R.<x> = PolynomialRing(Fp2)

E_start = EllipticCurve(Fp2, [0,6,0,1,0])
E_start.set_order((p+1)^2, num_checks=0) 


two_i = generate_distortion_map(E_start)

P2=E_start(220737745801*i + 50222311055, 190367540881*i + 54017057412)
Q2=E_start(140405500965*i + 258042847301, 297210225013*i + 344888892331)
P3=E_start(354749614347*i + 280322752628, 85255872295*i + 255093011257)
Q3=E_start(187154306904*i + 79900133137, 220502934600*i + 334923255776)
check_torsion_points(E_start, a, b, P2, Q2, P3, Q3)

a2=6
a4=(227348106349*i+257259789242)
a6=(4035550462*i+119078416285)
EB=EllipticCurve(Fp2,[0,a2,0,a4,a6])
PB=EB(91970188975*i + 124693845086, 377253313719*i + 322377957916)
QB=EB(198072574684*i + 400866480110, 96532007619*i + 380763487262)

recovered_key = CastryckDecruAttack(E_start, P2, Q2, EB, PB, QB, two_i, num_cores=1)
print(recovered_key)

运行结果如下：

6

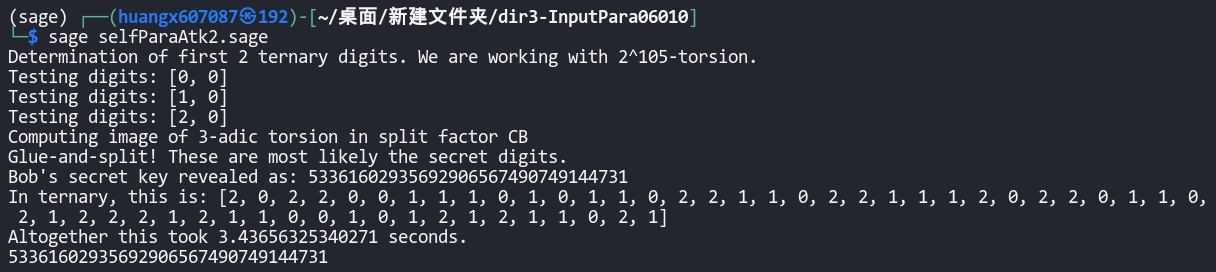
换一组参数试试，这次答案是 $53361602935692906567490749144731$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import public_values_aux
from public_values_aux import *

load('castryck_decru_shortcut.sage')

a, b = 110,67

p = 2^a*3^b - 1

public_values_aux.p = p
Fp2.<i> = GF(p^2, modulus=x^2+1)
R.<x> = PolynomialRing(Fp2)

E_start = EllipticCurve(Fp2, [0,6,0,1,0])
E_start.set_order((p+1)^2, num_checks=0) 


two_i = generate_distortion_map(E_start)

P2=E_start(56610319193701558658735766617880355615385547932040925880687156764*i + 42698419292581064688242589979397467965126090170436941878853866568, 35736771060022153096871481140526466092251776000496542458805572451*i + 1406713305674803984210143602460748242038256281655932542401586960)
Q2=E_start(87385346712865167405378671004116905429368722879634257587922373265*i + 20868980497449673695168909270503567045204488768234841927361424254, 93809470233601384687277542711720615096979514120814893736747406702*i + 102071080287673632345798509543832980678489137189256701006149797955)
P3=E_start(108340825021242044737371303329468146504320017600004306920882246903*i + 108396170192786465171102545295777043093136519196500623859843999594, 39510198811668974327487043561554886437520251439351004986533313590*i + 98384580631758549086105854565205076233552192646375463524786202427)
Q3=E_start(117708790334138506086639601581650847896208982849168647458602305949*i + 60171539076219076100859521953631698080351790640949638221590204795, 108234927295372521953904890581286233187456939597045817923583613193*i + 17111981949141181871590974861722205288395470270406688160159342438)
check_torsion_points(E_start, a, b, P2, Q2, P3, Q3)

a2=6 #usually to be six.
a4=(33352492415821181878007294686911877407020167370184992026961189883*i+360155498372969691801778829113065642920064704754943849117579719)
a6=(71078007951164850613906284431026209801045803425464743236950552863*i+60050844645541971863484821267140778695102640789034683181783646104)
EB=EllipticCurve(Fp2,[0,a2,0,a4,a6])
PB=EB(44655967089538875652566632875838189177891417754246765262862174361*i + 95761508234935577002311855392466107543835007665570312539644748521, 85321383142345971885193090537643266036849312093691332425107553101*i + 113017953225856300262660175780097470661672131417143141502018264468)
QB=EB (71214736694275496825585051349583527644008441002295381958581065547*i + 118100008118642712698371498755385508818364986084944574352354913594, 54703329181345516353291579273842096570542601384268943693078600755*i + 84401862403085750806051707190053760164677853749560631699068036990)

recovered_key = CastryckDecruAttack(E_start, P2, Q2, EB, PB, QB, two_i, num_cores=1)
print(recovered_key)

可以看到，得到的结果也很快

7

当然，也可以使用2.2节的代码进行测试。其中： E_start 为原始曲线，$P_2,Q_2,P_3,Q_3$ 对应2.2节代码中的 $P_A,Q_A,P_B,Q_B$，而这个代码中的 $E_B,P_B,Q_B$ 对应2.2节代码中的 $E_B,G_B,H_B$。

2.3.3 00010型曲线的攻击

在论文的第 5 章，我们得到了这样的内容，虽然翻译是机器翻译，但可以看到 $\phi_{2\mathrm i}$ 的映射表达式为：
$$
\phi_{2\mathrm i}: E(x,y)\rightarrow 2 E(-x,\mathrm iy)
$$
8

因此，对于曲线 $y^2=x^3+x$，上面的 two_i 可以这样写：

1
2
3
4
5
6
7
8
9
10
def two_i(Point):
    Ec=Point.curve()
    if(Point==Ec(0)):
        return Ec(0)
    else:
        xx,yy=Point[0],Point[1]
        xx=-xx
        yy=i*yy
        iPoint=Ec(xx,yy)
        return 2*iPoint

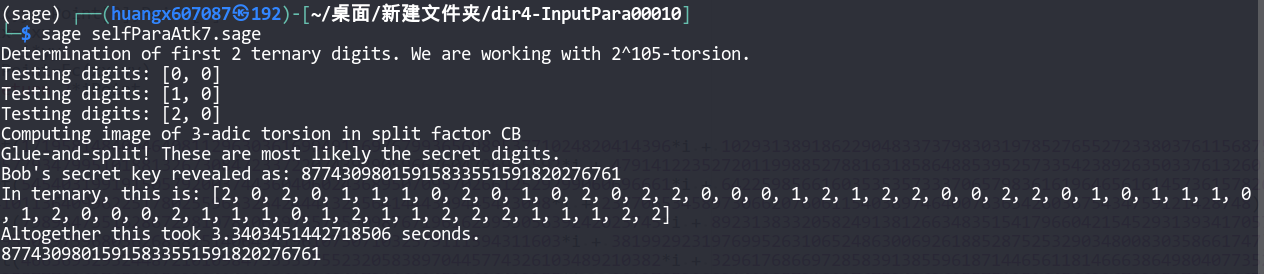
那么我们也可以得到攻击代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
import public_values_aux
from public_values_aux import *

load('castryck_decru_shortcut.sage')

a, b = 110,67

p = 2^a*3^b - 1 

public_values_aux.p = p
Fp2.<i> = GF(p^2, modulus=x^2+1)
R.<x> = PolynomialRing(Fp2)

E_start = EllipticCurve(Fp2, [0,0,0,1,0])
E_start.set_order((p+1)^2, num_checks=0) 

# Generation of the endomorphism 2i
def two_i(Point):
    Ec=Point.curve()
    if(Point==Ec(0)):
        return Ec(0)
    else:
        xx,yy=Point[0],Point[1]
        xx=-xx
        yy=i*yy
        iPoint=Ec(xx,yy)
        return 2*iPoint


P2=E_start(17195814840046408112963036169949156976799365698953771024820414396*i + 102931389186229048337379830319785276552723380376115687557503025718, 75778504057793479951018813267308472337220743929059667604796986592*i + 47914122352720119988527881631858648853952573354238926350337613260)
Q2=E_start(54540319919150579200374436040602436895070957026612529299060696661*i + 64225985661603535357333706579836161964656161457361578265449177285, 2267083341011364099622517802559653254244413235641444399445423098*i + 23770653458973066207606115403897464007836542603675434759121428748)
P3=E_start(7989847351628672981078106697557859098767196162395305639242023745*i + 89231383320582491381266348351541796604215452931393417057299686215, 99238707995304975968036268582514064981961075071032579111594311603*i + 38199292319769952631065248630069261885287525329034800830358661747)
Q3=E_start(4663695293244872101098475353375523205838970445774326103489210382*i + 32961768669728583913855961871446561181466638649804077352262661465, 52712260135577782637658195833849499206999684173146994531696493355*i + 90137853988314928573189276753486360557512526456632678305271362467)
check_torsion_points(E_start, a, b, P2, Q2, P3, Q3)


a2=0
a4=(102418828187774457761879456577153513507915057359277718737712550111*i+31532950820601891722920142855587562494984182810592253153908855275)
a6=(81186662414448050665979201453065315156725879839182514894602516221*i+114855290460797749422119777020804067441781626139255389813090673539) 
EB=EllipticCurve(Fp2,[0,a2,0,a4,a6])
PB=EB(41424643566869521367632949668986202694950053240719386036239671784*i + 97100535686874659598560862233789138506102606757930590165770050211, 28478553207476926857405639847764592248944426695136614829558619038*i + 57112427683516687662270959498666544806334396087049034869773482261)
QB=EB(83903916904730001170172551063303069216164579013051205895824540388*i + 94290363880834426978339452165347196781962782250248107794345225206, 89180000462470351871791116928719101870428228473355925736419881028*i + 95407185118153375790239945730336656643579227622240889452855365824)

#87743098015915833551591820276761

recovered_key = CastryckDecruAttack(E_start, P2, Q2, EB, PB, QB, two_i, num_cores=1)
print(recovered_key)

运行结果如下：

9

2.9 总结与回顾

2.9.1 同源曲线的求法

2同源
1
2
3
4
5
p=2**8*3**5-1
F.<img>=GF((p,2),modulus=[1,0,1])
E=EllipticCurve(F,[1,0])
P=E(img,0)
E.isogeny(P).codomain().j_invariant()
3同源
1
2
3
4
5
p=2**8*3**5-1
F.<img>=GF((p,2),modulus=[1,0,1])
E=EllipticCurve(F,[1,0])
P=E(54897,40274)
E.isogeny(P).codomain().j_invariant()
混合同源

需要注意的是，混合同源必须加 algorithm='factored'，否则会非常慢，并且内存还会被卡爆。。。

1
2
3
4
5
6
p=2**8*3**5-1
F.<img>=GF((p,2),modulus=[1,0,1])
E=EllipticCurve(F,[1,0])
P=E(42926*img + 1887, 60021*img + 14976)
E.isogeny(P).codomain().j_invariant()
#4485*img + 58033

2.9.2 SIDH的应用

已知通信双方的参数如下，flag为双方共享秘密值的实部的md5，包上flag提交。

1
2
3
4
5
6
7
8
9
10
alph,beta = 191,118
p = 2**alph*3**beta-1
Cp.<img> = GF(p**2,modulus=[1,0,1])
E = EllipticCurve(Cp,[1,0])
xa = 584496555152977952263051187264513064651276067462422849897
xb = 37682757929733147743730633501689839022920301898548500220
Pa = (3890173385494077585786113518802477300671812804735903208231728641198015042926576919967486058477584860965263321449*img + 584828209842877103640744000896095339777363670631877394059372721680411559677189054661820559515040199234170221817651, 410509288765605099029167660119172995772205248635741021443348197514620983285967575552293060720294469867982349678659*img + 548930165860799787670196445655670316785292043986372282652343383518446174454396640035137367946163853876973452753668)
Qa = (421604690831879517745604871374938409034817312564753376151016104663541612478690914420681512561903274599781004629482*img + 86871671015996107147496820435983909507668991378550122772712016787149157410753495265887407752063557661771605943910, 180160609497005981465811172297833341634318706104256987203386737689308641065089877175010097208331147293242130238056*img + 197151342217785322710468346320690864703187559637211131744844465191227679295619198257889036196666751765532255326047)
Pb = (432246268507304620615765479255840099513607930320042189132113053467777111887959352975167229337223218153317644975096*img + 258234009763233650750196421111785919206795442836176639412780414960329244931088103699224563002378692257321514631566, 433353153375662377686506321322284787451502853238565773205137821971198303160453015591068400935600894496365212830590*img + 292313742846902851874437028342611928684224606688812088787816579414266084838339385752295076820697862252252546861994)
Qb = (272086612765181657253335814356130852004060861562928627633629971852828122421021509993471606010508380202640765560265*img + 46012656019163765219488619336710432956068583297368188950052950196080786770580284615473738417777040081328154808021, 608201375956852861960569561164278611354036955015273398439040772149007105116277599617924113376019067039282284399710*img + 315116752107370746379770489489641864422673846221948079905427534744354763665649013882058862200076096765012230361516)

既然私钥都给你了，那直接走流程得了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
from random import *
alph,beta = 191,118
p = 2**alph*3**beta-1
Cp.<img> = GF(p**2,modulus=[1,0,1])
E = EllipticCurve(Cp,[1,0])
xa = 584496555152977952263051187264513064651276067462422849897
xb = 37682757929733147743730633501689839022920301898548500220
Pa = E(3890173385494077585786113518802477300671812804735903208231728641198015042926576919967486058477584860965263321449*img + 584828209842877103640744000896095339777363670631877394059372721680411559677189054661820559515040199234170221817651, 410509288765605099029167660119172995772205248635741021443348197514620983285967575552293060720294469867982349678659*img + 548930165860799787670196445655670316785292043986372282652343383518446174454396640035137367946163853876973452753668)
Qa = E(421604690831879517745604871374938409034817312564753376151016104663541612478690914420681512561903274599781004629482*img + 86871671015996107147496820435983909507668991378550122772712016787149157410753495265887407752063557661771605943910, 180160609497005981465811172297833341634318706104256987203386737689308641065089877175010097208331147293242130238056*img + 197151342217785322710468346320690864703187559637211131744844465191227679295619198257889036196666751765532255326047)
Pb = E(432246268507304620615765479255840099513607930320042189132113053467777111887959352975167229337223218153317644975096*img + 258234009763233650750196421111785919206795442836176639412780414960329244931088103699224563002378692257321514631566, 433353153375662377686506321322284787451502853238565773205137821971198303160453015591068400935600894496365212830590*img + 292313742846902851874437028342611928684224606688812088787816579414266084838339385752295076820697862252252546861994)
Qb = E(272086612765181657253335814356130852004060861562928627633629971852828122421021509993471606010508380202640765560265*img + 46012656019163765219488619336710432956068583297368188950052950196080786770580284615473738417777040081328154808021, 608201375956852861960569561164278611354036955015273398439040772149007105116277599617924113376019067039282284399710*img + 315116752107370746379770489489641864422673846221948079905427534744354763665649013882058862200076096765012230361516)

def pkGen(P,Q,Po,Qo,x,Ec):
    S = P+x*Q
    phi =  Ec.isogeny(S,algorithm="factored")
    E1 = phi.codomain()
    return E1,phi(Po),phi(Qo)

def getSecret(Ec,P,Q,x):
    Key = P+x*Q
    phi =  Ec.isogeny(Key,algorithm="factored")
    return phi.codomain().j_invariant()

xa = 225902606209514408534212339057054
xb = 38410379124791756271891302485727
print('xa =',xa)
print('xb =',xb)

Ea,Ga,Ha = pkGen(Pa,Qa,Pb,Qb,xa,E)
Eb,Gb,Hb = pkGen(Pb,Qb,Pa,Qa,xb,E)
print(f'Ea : {Ea}')
print(f'Ga = {Ga.xy()}\nHa = {Ha.xy()}')
print(f'Eb : {Eb}')
print(f'Gb = {Gb.xy()}\nHb = {Hb.xy()}')

Keya = getSecret(Eb,Gb,Hb,xa)
print('Keya =',Keya)
Keyb = getSecret(Ea,Ga,Ha,xb)
print('Keyb =',Keyb)
assert Keya==Keyb
#Keyb = 600914791934031108627236809762877964673080416128475550460621517207409205713986769743394408671974542775613351353324*img + 491526678134851661327546821730369546969882065407965884271380638078279282963613533645664886114161991306616597283726

得到实部和flag：

1
2
re_Key=491526678134851661327546821730369546969882065407965884271380638078279282963613533645664886114161991306616597283726
#flag{009f92859d97ee0cc29fa04c53a2d228}

2.9.3 SIDH的破解

已知双方的参数如下，flag为双方共享秘密值的实部的md5，提交时请包上flag。

1
2
3
4
5
6
7
8
9
10
11
12
Pa = (232356258387014843308023791594194948039653666270340137835215927250973352859489298612585996169258523678050720878068*img + 538744669524057459396126178584247908817270647700116142476958188100924860869364698166826434756090268295618493824546, 76249308728653875112262060006464245936500586952836731644982931835700736654603945269238982425772488453412959020256*img + 422527598392474246465781364581068979648811682741474158269303182554106577514707994762230052567207331356617986793857)
Qa = (461734419938992457897474506658120518854728597703342582171065611938696479104616816841422560219140242714052457098039*img + 428777625865071874615044976213650933847002825156453497653669798891114414242384057758719743544296087508587555797906, 10662506168648652077262377015475872318520888157151447996364468881456198789398711652111802781610471467541371693871*img + 290637079464465563854589563245667563508278272984878411820236219409522261330414289096025057004409258153467308935585)
Pb = (136531171239478416253478572405792254497808491771514926079758453336517795761809532657725981910759601494892554255815*img + 547772446087952417016962537233369245145574866103039586455592266296446663680113698888179763744579786018164571857789, 457116649679592092763069582858437567765320891705891320551968559771374785456259433916225623550934992991299947284413*img + 220741477630185661756935255926737927348327841672351013800906282912811102990934707604736714895606762660312432200585)
Qb = (68285232547217881547351504529947636670204344614106430836226815201213976201473256324305226432972069335362227146188*img + 536563314649157588596255866356195792762142377066728743466380118620513054320726201375156880198801968916974384042962, 363547187548222899213877620074284830292371238932649724761157743295775312969628273623976808527586196308395098178602*img + 272864944055789579262784896184113492423488480672733346446670727958326171151270072235303789238157891259626005445814)
Eaa=553682304507170323694909479540159141417415955361357480550799039311002385510550740752642326777321790980623523493618*img + 617204275340906100098189128620612063894313851251833742088080508523155065989972960267092144352740575071678117964243
Eab=455319914313033939950132208386200653229055945097693853960296206618800901577191133231392650871295833537081485368870*img + 122442073359944268452731987876446768163247246045006139338145290536847351330281787685128240636078590905784113828395
Eba=325722253892019113276309344646772167140590893668313301180238023235229797514844218553269918097608427893375003138452*img + 364270281373947456485003876763533510032823702499784502493467975510883184423512855706767845689661428270907087419026
Ebb=368957767183452800630213316562881012761387625350286469658089964678523255885821818036490144483399922929140979711679*img + 359419267440966895576472888036339417074452010830491937875437874289887554146948963898485122900228028669459279474529
Ga = (153670688481774722286956654029987219016687216553982800489606486945669825176519237609374444750315392581331453200224*img + 623060232942591104056079987617666202027202833171675169068238715705747183738658800714190048981144792972700161906537, 587139501470612673184356690938039262515816479119557107398452643412923423690960896384919509254181855826626543517986*img + 615397222267594041179990468005784465011158277313570177564752638027537250079707783104979650283511075968620845092979)
Ha = (572256162523445816598267038194968718644629027347119865886298198303092647830438487232425965009682510295148114056297*img + 347630821234807351437681064298041150986195714012763279973087493362352128919324539002908704100913234567613820995448, 168032604174726367019704754252432387372078869031615543238298628511922361054410486212916907158680156418555327562362*img + 195078545071409123139535697181234107195041739039568432194147323773165454434922400709340833348621727077039212579920)
Gb = (356227378788641743509166000768130466712202970744409874232458742609596386253989869973740201630946581452040741428639*img + 558014234250449098056063541268876689941344717355915519165892535333619665322441592696609809029747124612249582373156, 284144268137151820525929014178749815068614681892333440370507567215815474226518660202916471160867182787574588170641*img + 212102089516189626564035487979707055529919235208811222451802967430628679346175546185728324374383815991910663869615)
Hb = (601988875242491627127640698692267933775219799173095669566547148085539575370045236378970737028724933965940811427576*img + 436748337066570764146405402437969684420374112222582333951194222947651522571935238521748503214722377113959956040093, 10753745263084186335835932573522446169706265222930403707093876926454456847704756026904213851136493771042813451783*img + 60129011706640901710199282670283493071879841414421196718045933440982829728050225324274407299746630855119033164322)

这个题给了SIDH的公共参数，但私钥未知，我们的目标是求出最终能双方共享的秘密值。直接一把梭了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
import public_values_aux
from public_values_aux import *

load('castryck_decru_shortcut.sage')

a, b = 191,118

p = 2^a*3^b - 1 

public_values_aux.p = p
Fp2.<img> = GF(p^2, modulus=x^2+1)
R.<x> = PolynomialRing(Fp2)

E_start = EllipticCurve(Fp2, [0,0,0,1,0])
E_start.set_order((p+1)^2, num_checks=0) 

# Generation of the endomorphism 2i
def two_i(Point):
    Ec=Point.curve()
    if(Point==Ec(0)):
        return Ec(0)
    else:
        xx,yy=Point[0],Point[1]
        xx=-xx
        yy=Fp2([0,1])*yy
        iPoint=Ec(xx,yy)
        return 2*iPoint

E0=E_start

P2 = E0(232356258387014843308023791594194948039653666270340137835215927250973352859489298612585996169258523678050720878068*img + 538744669524057459396126178584247908817270647700116142476958188100924860869364698166826434756090268295618493824546, 76249308728653875112262060006464245936500586952836731644982931835700736654603945269238982425772488453412959020256*img + 422527598392474246465781364581068979648811682741474158269303182554106577514707994762230052567207331356617986793857)
Q2 = E0(461734419938992457897474506658120518854728597703342582171065611938696479104616816841422560219140242714052457098039*img + 428777625865071874615044976213650933847002825156453497653669798891114414242384057758719743544296087508587555797906, 10662506168648652077262377015475872318520888157151447996364468881456198789398711652111802781610471467541371693871*img + 290637079464465563854589563245667563508278272984878411820236219409522261330414289096025057004409258153467308935585)
P3 = E0(136531171239478416253478572405792254497808491771514926079758453336517795761809532657725981910759601494892554255815*img + 547772446087952417016962537233369245145574866103039586455592266296446663680113698888179763744579786018164571857789, 457116649679592092763069582858437567765320891705891320551968559771374785456259433916225623550934992991299947284413*img + 220741477630185661756935255926737927348327841672351013800906282912811102990934707604736714895606762660312432200585)
Q3 = E0(68285232547217881547351504529947636670204344614106430836226815201213976201473256324305226432972069335362227146188*img + 536563314649157588596255866356195792762142377066728743466380118620513054320726201375156880198801968916974384042962, 363547187548222899213877620074284830292371238932649724761157743295775312969628273623976808527586196308395098178602*img + 272864944055789579262784896184113492423488480672733346446670727958326171151270072235303789238157891259626005445814)
check_torsion_points(E_start, a, b, P2, Q2, P3, Q3)

a4=325722253892019113276309344646772167140590893668313301180238023235229797514844218553269918097608427893375003138452*img + 364270281373947456485003876763533510032823702499784502493467975510883184423512855706767845689661428270907087419026
a6=368957767183452800630213316562881012761387625350286469658089964678523255885821818036490144483399922929140979711679*img + 359419267440966895576472888036339417074452010830491937875437874289887554146948963898485122900228028669459279474529

EB = EllipticCurve(Fp2, [a4, a6])
PB = EB(356227378788641743509166000768130466712202970744409874232458742609596386253989869973740201630946581452040741428639*img + 558014234250449098056063541268876689941344717355915519165892535333619665322441592696609809029747124612249582373156, 284144268137151820525929014178749815068614681892333440370507567215815474226518660202916471160867182787574588170641*img + 212102089516189626564035487979707055529919235208811222451802967430628679346175546185728324374383815991910663869615)
QB = EB(601988875242491627127640698692267933775219799173095669566547148085539575370045236378970737028724933965940811427576*img + 436748337066570764146405402437969684420374112222582333951194222947651522571935238521748503214722377113959956040093, 10753745263084186335835932573522446169706265222930403707093876926454456847704756026904213851136493771042813451783*img + 60129011706640901710199282670283493071879841414421196718045933440982829728050225324274407299746630855119033164322)

recovered_key = CastryckDecruAttack(E0, P2, Q2, EB, PB, QB, two_i, num_cores=1)
print(recovered_key)

#130137520256908336013846031813998340229884778157326738560

拿到私钥后，就很简单了，走流程就OK:)

1
2
3
4
5
6
7
8
def getSecret(Ec,P,Q,x):
    Key = P+x*Q
    phi =  Ec.isogeny(Key,algorithm="factored")
    return phi.codomain().j_invariant()
Keyb = getSecret(Ea,Ga,Ha,xb)
#286484023462990024388767738992220658539990531124243560958273105209745510296092203267044512042937339103529646662711*img + 463300547852541792624117140690457946141975681947394080567603424013510602721865680807115515306481798621521396935288
#Re(Keyb)=463300547852541792624117140690457946141975681947394080567603424013510602721865680807115515306481798621521396935288
#flag{a8e4cc996fde401891f9a125412fdd76}

3.CSIDH预备知识

当然，CSIDH的预备知识还是需要的:)

REF：CSIDH 的论文 383.pdf (iacr.org)

3.1 CISDH基本思想

在SIDH中，我们使用的曲线是定义在二次扩域 $\mathbb C_p=\mathbb Z_{p}+\mathrm i\mathbb Z_{p}$ 上的超奇异椭圆曲线，其中 $p=2^\alpha3^\beta k-1$，该曲线总是有两个生成元 $P_0,Q_0$。因此通信双方可以基于 $P_0,Q_0$，选择阶为 $2^\alpha$ 和 $3^{\beta}$ 的基点 $P_A,Q_A,P_B,Q_B$ 并进行密钥交换过程。

而在CSIDH中，我们选择的是一次域 $\mathbb F_p$ 上的超奇异曲线，其中 $p+1$ 是很多小素数 $\ell_1,\ell_2,…,\ell_n$ 的乘积。设 $E$ 为所选取的曲线，由于 $E$ 的超奇异性，那么 $E$ 的阶就是 $p+1$，因此对于 $E$ 上的任意点 $P$，均存在 $\ell_1P,\ell_2P,…,\ell_nP$ ，使得 E2=E.isogeny(ell[i]*P) 存在。

很显然，既然 $E$ 是超奇异的，那么 $E_2$ 也是超奇异的，所以 $E_2$ 的阶仍然为 $p+1$，那么设 $P_2$ 是 $E_2$ 的生成元，那么还可以继续做 E3=E2.isogeny(ell[i]*P2)，以此类推。CSIDH就是这样的思想。

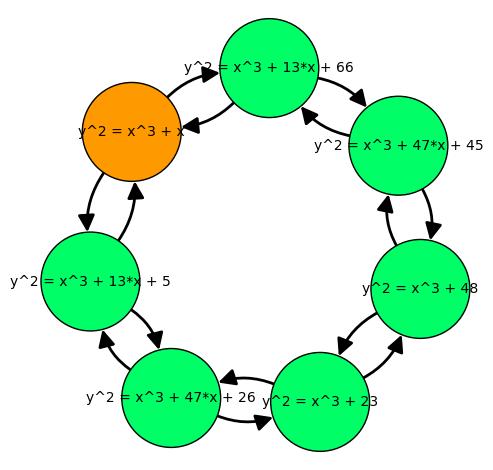
3.2 同源图(蒙哥马利型)

对于一个域 $K$ 和素数 $\ell$，其中 $\ell$ 不是 $K$ 的特征（$\mathrm{char} K$）的因数，那么 $K$ 有理 $\ell$ 同源图中，顶点所有在 $K$ 上定义的椭圆曲线。对于两个曲线 $E_1,E_2$ 中的每个 $K$ 有理 $\ell$ 同源，都会有一条有向边 $(E_1,E_2)$。

11

Sage画图代码：

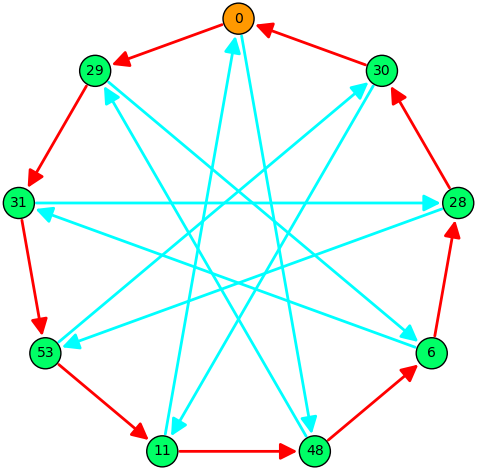
1
2
3
4
5
6
7
8
9
10
E=EllipticCurve(GF(71),[1,0])
G=E.isogeny_ell_graph(3)

D={'#ff9900':[],'#00ff66':[]}
for i in G.vertices():
    if(i=='y^2 = x^3 + x'):
        D['#ff9900'].append(i)
    else:
        D['#00ff66'].append(i)
plot(E.isogeny_ell_graph(3),vertex_labels=True,edge_labels=True,vertex_size=5000,edge_thickness=4,vertex_colors=D)

上面那就是一个 $\mathbb Z_{71}$ 上的度为 $3$ 同源图，我们可以看出其构成了一个循环，$y^2=x^3+47x+45$ 具有两个 $3$ 同源： $y^2=x^3+13x+66$ 和 $y^2=x^3+48$，Sage中也提供了内置函数供查询：

1
2
3
4
5
6
E=EllipticCurve(GF(71),[47,45])
E.isogenies_prime_degree(3)
"""
[Isogeny of degree 3 from Elliptic Curve defined by y^2 = x^3 + 47*x + 45 over Finite Field of size 71 to Elliptic Curve defined by y^2 = x^3 + 48 over Finite Field of size 71,
 Isogeny of degree 3 from Elliptic Curve defined by y^2 = x^3 + 47*x + 45 over Finite Field of size 71 to Elliptic Curve defined by y^2 = x^3 + 59*x + 47 over Finite Field of size 71]
 """

当然，这个图有什么作用呢？很显然，根据我们现在奶所讲的内容，似乎也不太好解释。但我们可以先回顾我们之前的工作：对于一个椭圆曲线而言，我们似乎不停地在关注它的 ”j-不变量“ 和 ”蒙哥马利曲线形式“（重点是 E.montgomery_model().a2() 的值），那么我们也来写一个实验代码测一下：

1
2
3
4
5
6
7
8
9
10
11
12
13
Para=[[1,0],[13,66],[47,45],[0,48],[0,23],[47,26],[13,5]]
Es=[EllipticCurve(GF(71),Para[i]) for i in range(7)]
for i in range(len(Es)):
    print(Es[i].j_invariant(),Es[i].montgomery_model().a2())
"""
24 0
66 35
41 58
0 28
0 43
41 13
66 36
"""

可以看出，如果我们从 $y^2=x^3+x$ 曲线对应的点为中心，会发现相互对称的两条曲线的 j-不变量相同，但蒙哥马利曲线参数却不同。并且，如果再注意看蒙哥马利曲线参数，会发现与 $y^2=x^3+x$ 节点对称的两点，其蒙哥马利曲线参数互为相反数。

3.3 二次扭曲

在代数几何的数学领域中，特征不为 $2$ 的域 $K$ 上的椭圆曲线 $E$ 具有相关的二次扭曲，即另一条椭圆曲线 $E_2$ 与 $K$ 的代数闭包上的 $E$ 同构。具体而言，椭圆曲线之间的同构是 $1$ 阶同源，即可逆同源。曲线及其扭曲具有相同的 j-不变量。（REF：维基百科）

而所谓二次扭曲，我们可以设 $d≠0$，且 $d$ 是 $p$ 的非二次剩余，那么曲线 $E:y^2=x^3+ux^2+ax+b$ 的二次扭曲的形式为 $E^d:dy^2=x^3+ux^2+ax+b$ ，或 $E^d:y^2=x^3+dux^2+d^2ax+d^3b$。因此，两条曲线上的映射满足：
$$
\phi:E(x,y)\rightarrow E_2\left(\dfrac{x}{d},\dfrac{y}{d\sqrt d }\right)
$$

我们来看下面的代码（E2.a_invariants() 显示 [a1,a2,a3,a4,a6] 五个值，用于简化椭圆曲线的显示）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Para=[[1,0],[13,66],[47,45],[0,48],[0,23],[47,26],[13,5]]
Es=[EllipticCurve(GF(71),Para[i]) for i in range(7)]
E=Es[2]
print(E.j_invariant())
for i in range(4):
    E2=E.quadratic_twist()
    print(E2.a_invariants(),E2.montgomery_model().a2(),E2.j_invariant(),E.is_isomorphic(E2))
"""
41
(0, 0, 0, 52, 59) 13 41 False
(0, 0, 0, 28, 52) 13 41 False
(0, 0, 0, 21, 22) 13 41 False
(0, 0, 0, 23, 56) 13 41 False
"""

print(E.change_ring(GF(71**2)).is_isomorphic(E2.change_ring(GF(71**2))))
#True

可以发现，我们只说了 $d$ 是 $p$ 的二次非剩余一个条件，因此每次Sage会随机选取 $d$，但这些曲线你的蒙哥马利参数竟然全是 $13$，而我们所选取的曲线的蒙哥马利参数恰好相反！似乎就是图中关于 $y^2=x^3+x$ 节点的对称点！并且这两条曲线的j-不变量相同。但这两条曲线却不同构，难道理论出问题了吗？

那为啥叫二次扭曲呢？因为 $E$ 和 $E_2$ 在 $\mathbb F_{p^2}$ 上同构！这同时说明 j-不变量 判定同构的方法，只在二次扩域中有用！

如果对一个曲线 E 计算两次二次扭曲会怎样呢，下面的代码告诉了我们答案：我们又回到了原来的曲线中去了！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Para=[[1,0],[13,66],[47,45],[0,48],[0,23],[47,26],[13,5]]
Es=[EllipticCurve(GF(71),Para[i]) for i in range(7)]
E=Es[2]
print(E.j_invariant())
for i in range(4):
    E2=E.quadratic_twist().quadratic_twist()
    print(E2.a_invariants(),E2.montgomery_model().a2(),E2.j_invariant(),E.is_isomorphic(E2))
"""
41
(0, 0, 0, 39, 16) 58 41 True
(0, 0, 0, 46, 5) 58 41 True
(0, 0, 0, 11, 27) 58 41 True
(0, 0, 0, 62, 38) 58 41 True
"""

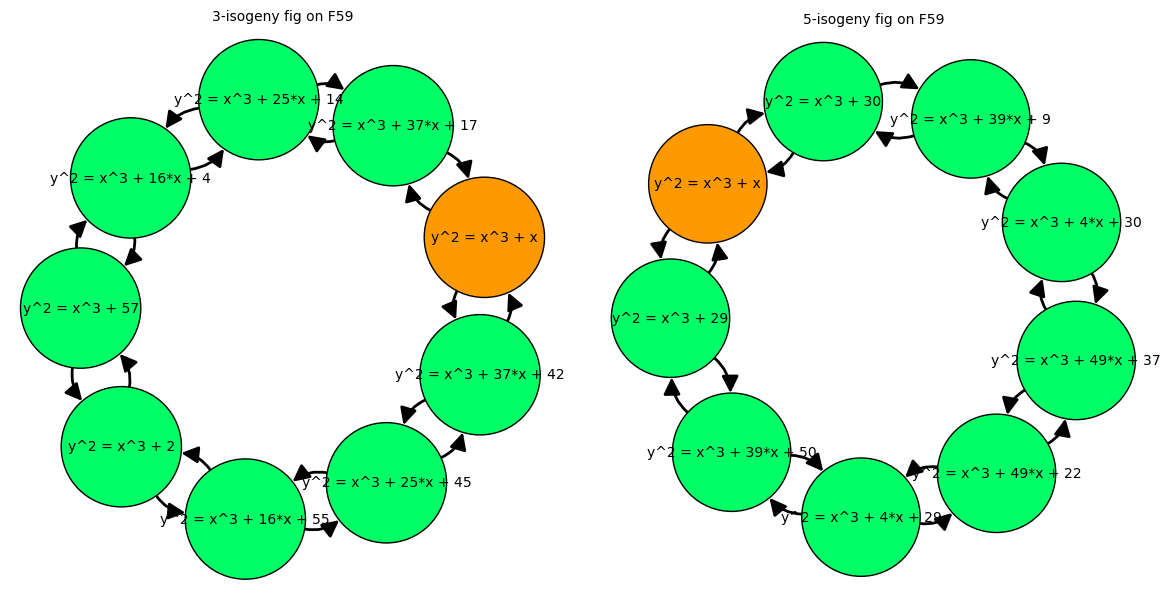
3.4 $\mathbb F_{59}$ 和 $\mathbb F_{419}$ 上的超奇异曲线

让我们再回顾一下我们刚才提到的内容：既然CSIDH是多个素数，那么我们以 $\ell_1=3,\ell_2=5$ 为例，取 $p=59$，来看看会发生什么。

12

Sage画图代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
>E=EllipticCurve(GF(59),[1,0])
>G3=E.isogeny_ell_graph(3)
>G5=E.isogeny_ell_graph(5)
>D={'#ff9900':[],'#00ff66':[]}
>for i in G3.vertices():
if(i=='y^2 = x^3 + x'):
    D['#ff9900'].append(i)
else:
    D['#00ff66'].append(i)
>S3=plot(G3,title=r'3-isogeny fig on F59',vertex_labels=True,edge_labels=True,vertex_size=5000,edge_thickness=4,vertex_colors=D)
>D={'#ff9900':[],'#00ff66':[]}
>for i in G5.vertices():
if(i=='y^2 = x^3 + x'):
    D['#ff9900'].append(i)
else:
    D['#00ff66'].append(i)
>S5=plot(G5,title=r'5-isogeny fig on F59',vertex_labels=True,edge_labels=True,vertex_size=5000,edge_thickness=4,vertex_colors=D)
>S=graphics_array([S3,S5])
>S.show(figsize=[12,12])

我们随后来计算一下上面所有曲线的蒙哥马利参数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
p=59
E3s=[[1,0],[37,42],[25,45],[16,55],[0,2],[0,57],[16,4],[25,14],[37,17]]
E5s=[[1,0],[0,30],[39,9],[4,30],[49,37],[49,22],[4,29],[39,50],[0,29]]
for i in range(len(E3s)):
    E3s[i]=EllipticCurve(GF(p),E3s[i])
for i in range(len(E5s)):
    E5s[i]=EllipticCurve(GF(p),E5s[i])
seq3,seq5=[],[]
for i in range(len(E3s)):
    seq3.append(E3s[i].montgomery_model().a2())
for i in range(len(E5s)):
    seq5.append(E5s[i].montgomery_model().a2())
print(seq3)
print(seq5)
#[0, 30, 28, 6, 48, 11, 53, 31, 29]
#[0, 48, 29, 6, 31, 28, 53, 30, 11]

你会发现，上下两排输出的内容似乎是相同的，只不过顺序不同，那么我们可以从节点 0 开始引线，红线是 3-同源的顺序，蓝线是 5-同源的顺序。

13

注1：几乎所有情况下，同源图是双向有向图，也就是 $0$ 到 $29$ 有一条边，那么 $29$ 到 $0$ 也有一条边，这里我们画成单项变，是为后面规定 正方向用的，箭头方向为同源计算的正方向，逆着箭头走为负方向。

注2：上一条也有2种不成立的情况，在这种情况下，$0$ 的出边多于入边。这2种情况为：设曲线 $E$ 在域 $K$ 上定义，此时

  1. $E$ 的 j-不变量为 $0$ 且 $\sqrt{-3}\in K$。
  2. $E$ 的 j-不变量为 $1728$ 且 $\sqrt{-1} \in K$。

因此，在这种限制下，模数选取需要满足要求：$p\equiv 11\pmod{12}$。

Sage 画图代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
p=59
E0=EllipticCurve(GF(p),[1,0])
def get(E,x):
 m = 0
 res=[E.montgomery_model().a2()]
 while(1):
     G = choice(E(0).division_points(x)[1:])
     E = E.isogeny(G).codomain()
     if(E.montgomery_model().a2()==res[0]):
         return res
     else:
         res.append(E.montgomery_model().a2())
seq3=get(E0,3)
seq5=get(E0,5)
Gr = DiGraph({}, loops=True, multiedges=True, sparse=True)
for i in range(len(seq3)):
    Gr.add_edges([(seq3[i],seq3[(i+1)%len(seq3)],'3')])
for i in range(len(seq5)):
    Gr.add_edges([(seq5[i],seq5[(i+1)%len(seq5)],'5')])
Col={'#ff9900':[0],'#00ff66':seq3[1:]}
Dpos={}
for i in range(len(seq3)):
    x = float(cos(pi/2 + ((2*pi)/len(seq3))*i))
    y = float(sin(pi/2 + ((2*pi)/len(seq3))*i))
    Dpos[seq3[i]]=(x,y)
Gr.graphplot(edge_labels=False,color_by_label=True,vertex_size=500,vertex_colors=Col,pos=Dpos).plot()

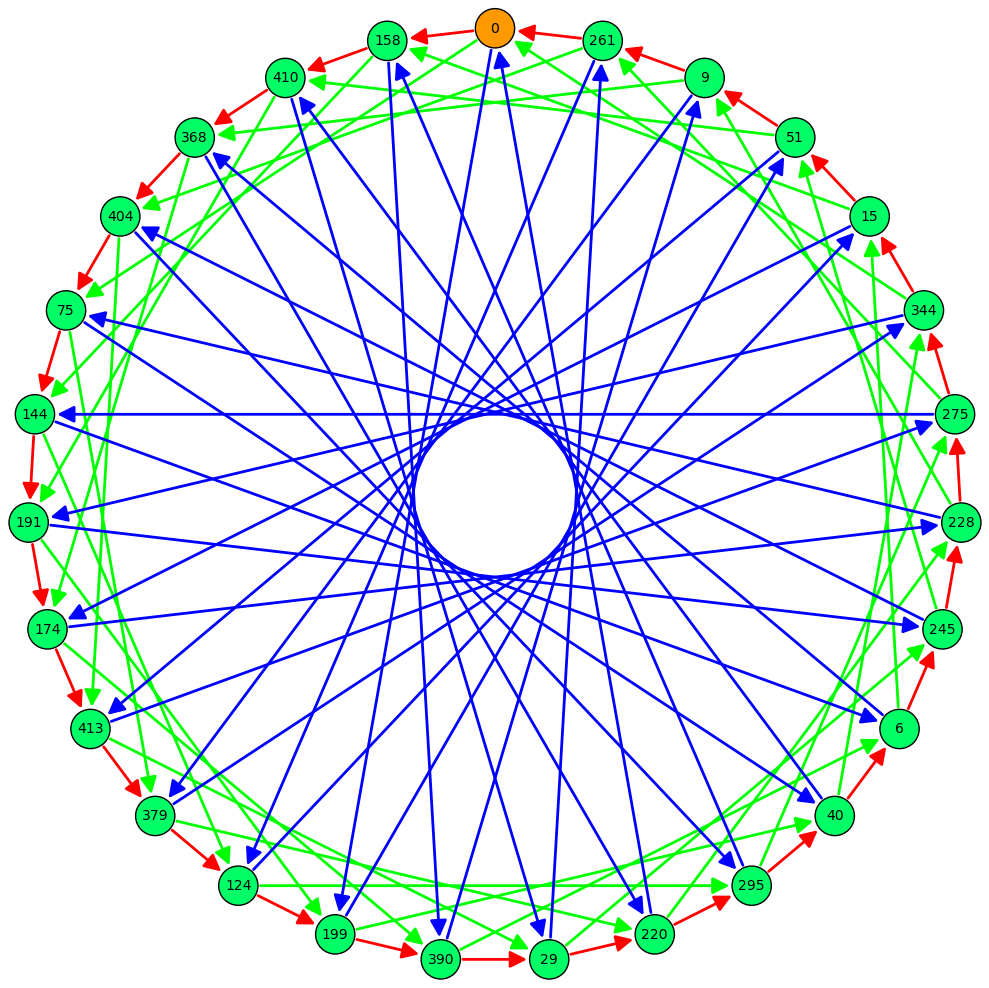
然后也有一个 $419$ 的 图也可以参考一下，红色的线为 $3$-同源，蓝色的线为 $5$-同源，绿色的线为 $7$-同源。可以发现，$3$-同源和 $7$-同源的阶均为 $27$，而 $5$-同源的阶为 $9$。

14

Sage 画图代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
p=419
E0=EllipticCurve(GF(p),[1,0])
def get(E,x):
    m = 0
    res=[E.montgomery_model().a2()]
    while(1):
        G = choice(E(0).division_points(x)[1:])
        E = E.isogeny(G).codomain()
        if(E.montgomery_model().a2()==res[0]):
            return res
        else:
            res.append(E.montgomery_model().a2())
seq3=get(E0,3)
seq5=get(E0,5)
seq52=get(EllipticCurve(GF(p),[0,158,0,1,0]),5)
seq53=get(EllipticCurve(GF(p),[0,261,0,1,0]),5)

seq7=get(E0,7)
Gr = DiGraph({}, loops=True, multiedges=True, sparse=True)
for i in range(len(seq3)):
       Gr.add_edges([(seq3[i],seq3[(i+1)%len(seq3)],'3')])
for i in range(len(seq5)):
       Gr.add_edges([(seq5[i],seq5[(i+1)%len(seq5)],'5')])
       Gr.add_edges([(seq52[i],seq52[(i+1)%len(seq52)],'5')])
       Gr.add_edges([(seq53[i],seq53[(i+1)%len(seq53)],'5')])
for i in range(len(seq7)):
       Gr.add_edges([(seq7[i],seq7[(i+1)%len(seq7)],'7')])
Col={'#ff9900':[0],'#00ff66':seq3[1:]}
Dpos={}
for i in range(len(seq3)):
       x = float(cos(pi/2 + ((2*pi)/len(seq3))*i))
       y = float(sin(pi/2 + ((2*pi)/len(seq3))*i))
       Dpos[seq3[i]]=(x,y)
Gr.graphplot(edge_labels=False,color_by_label=True,vertex_size=500,vertex_colors=Col,pos=Dpos).plot()

如果我们规定上图从 $0$ 引出的线中，箭头方向为正方向的话，那么密钥双方可以互相约定走法，是正着走还是反着走，那么只需要双方约定好这个参数，双方走的内容一样，那不就能够得到相同的值了吗。

3.9 总结与回顾

3.9.1 求 $p$ 同源的蒙哥马利参数

1
2
3
4
E=EllipticCurve(GF(419),[1,0])
G=(E(0).division_points(7))[2]
phi=E.isogeny(G)
phi.codomain().montgomery_model().a2()

3.9.2 求 $p$ 同源的阶

1
2
3
4
5
6
7
8
9
10
11
p = 419
E = EllipticCurve(GF(p), [1, 0])
j = E.j_invariant()
m = 0
while 1:
    G = choice(E(0).division_points(3)[1:])
    E = E.isogeny(G).codomain()
    m += 1
    if E.j_invariant() == j:
        print(m)
        break

3.9.3 求不同 $p$ 同源复合的结果

1
2
3
4
5
6
7
8
9
p = 419
E = EllipticCurve(GF(p), [1, 0])
ells = [3, 5, 7]
key = [3, -4, 4]
for ell,k in zip(ells,key):
    for i in range(k):
        G = choice(E(0).division_points(ell)[1:])
        E = E.isogeny_codomain(G)
E.montgomery_model().a2()

3.9.4 给定曲线二次扭曲的求法

1
2
3
4
5
6
p = 419
E = EllipticCurve(GF(p), [1, 0])
G = choice(E(0).division_points(3)[1:])
E = E.isogeny_codomain(G)
E = E.quadratic_twist()
E.montgomery_model().a2()

4.CSIDH算法

4.1 方案简介

4.1.1 Setup

选择素数 $p\equiv 3\pmod 8$，实际上多使用 $p=4(\prod_{i=1}^n\ell_i)-1$，其中 $\ell_i$ 是不同的小素数，以及在 $\mathbb F_p$ 上拥有自同态 $O[\sqrt {-p}]$ 上的超奇异椭圆曲线 $E:y^2=x^3+x$。这里我们选择 $p=419$，其中 $\ell=3,5,7$，$n=3$。

1
2
3
4
ells=[3,5,7]
p=4*prod(ells)-1
F = GF(p)
E0 = EllipticCurve(F, [1, 0])

4.1.2 KeyGen + KeyExchange

通信双方Alice和Bob分别生成一个 $n$ 元组 $(e_1,e_2,…,e_n)$ 作为私钥，其中 $e_i\in[-m,m]\cap \mathbb Z$。我们假设 $m=5$。

1
2
ska=[2,5,-1]
skb=[0,-2,1]

随后，Alice按照 ska 的内容开始走线，Bob 按照 skb 的内容开始走线，最终双方会得到两条曲线 $E_A$ 和 $E_B$，Alice和Bob分别记录 $E_A$ 的蒙哥马利参数 $A$ 和 $E_B$ 的蒙哥马利参数 $B$，并发送给对方。

在收到对方的信息后，Alice 以 $y^2=x^3+Bx^2+x$ 为起点，Bob 以 $y^2=x^3+Ax^2+x$ 为起点，继续按照自己的参数走线，最后得到的曲线的蒙哥马利参数就是双方共享的密钥了！

在实际中，常常选取 $n=74$， $p=4(\prod_{i=1}^{74}\ell_i)-1$，其中 $\ell_1\sim\ell_{73}$ 为最小的 $73$ 个奇素数，$\ell_{74}=587$。此时 $p$ 为 $512$ 位素数，因此公钥的大小为 $64$ 字节。而私钥大小一般为 $37$ 字节，说明 $m$ 的值一般不超过 $±7$，这样才能在 $37$ 字节中塞入 $74$ 个数字。

CSIDH的代码其实非常简单，但理解起来挺难的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def csidh(A, priv):
    E = EllipticCurve(F, [0, A, 0, 1, 0])
    for sgn in [1, -1]:
        for e, ell in zip(priv, ells):
            for i in range(sgn * e):
                while not (P := (p + 1) // ell * E.random_element()):
                    pass
                E = E.isogeny_codomain(P)
        E = E.quadratic_twist()
    return E.montgomery_model().a2()
A = csidh(0,ska)
B = csidh(0,skb)
key1=csidh(B,ska)
key2=csidh(A,skb)
print(key1,key2)
#124 124

放个论文中对这部分的严谨说法
15

4.2 CSIDH的安全性

CSIDH是可证明量子安全的，在仅知道 $A,B$ 两个蒙哥马利参数的情况下，想要求出最终的秘密值是不可行的。其实可以看一下 $p=419$ 的那张图，秘密值相差一点，最后结果其实可以相差非常大，并且确实可以在 $m$ 很小的情况下，遍历完所有可能的取值。因此虽然SIDH被攻破了，但CSIDH目前尚未有有效的攻击方法（呃，如果这个被攻破，同源是不是就玩不起来了）。

4.3 CSIDH 例题选讲

4.3.1 SU_Auth

之前SUCTF出了一个SU_Auth，也是基于CSIDH的，来看一下（使用本地复现代码）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from Crypto.Cipher import AES
from ast import literal_eval
from hashlib import md5
import subprocess

ells = [*primes(3, 200), 269]
p = 4*prod(ells) - 1
F = GF(p)

SUKEY = [randint(-3, 3) for _ in range(len(ells))]
def SuAuth(A, priv, LIMIT=True):
    if any(priv[i] == SUKEY[i] for i in range(len(ells))) and LIMIT: return "🙅SUKEY"
    E = EllipticCurve(F, [0, A, 0, 1, 0])
    for sgn in [1, -1]:
        for e, ell in zip(priv, ells):
            for i in range(sgn * e):
                while not (P := (p + 1) // ell * E.random_element()) or P.order() != ell:
                    pass
                E = E.isogeny_codomain(P)
        E = E.quadratic_twist()
    return E.montgomery_model().a2()

cipher = lambda key: AES.new(md5(key.encode()).digest(),AES.MODE_ECB)
SUDOOR = cipher(str(SuAuth(0, SUKEY, 0))).encrypt(b"./OPEN_THE_FLAG!")
#P.S. 这个本地复现时，要写一个printf("flag{XXX}")的程序并编译， 程序命名为OPEN_THE_FLAG!
print("😜", SuAuth(0, SUKEY, 0))

while True:
    AKey = SuAuth(0, literal_eval(input("🔑: ")))
    try: subprocess.run(cipher(str(AKey)).decrypt(SUDOOR))
    except: continue

我们本地测一下，会发现连上去之后，跑得非常慢，10秒才给出flag的加密值。

可以看到SUAuth中的执行过程，如果给出的KEY和SUKEY中的任何一个分量相对应，那么服务器会直接返回，不会执行后面的内容。并且程序语言执行时，一定是存在逻辑短路的，any 就相当于有一个成立久会返回。考虑到从连上到收到flag的密文用了10秒，刨去参数初始化和连接耗时，说明执行SUAuth函数至少需要 $3$ 秒以上 ，因此应该可以通过时间去判断条件成立。

由于 SUKEY 每个分量的值是 $-3$ 到 $3$，我们可以发现，发送一个全 $2$ 的Key，本地 2ms 就收到了返回结果，而发送一个全 $4$ 的Key，本地 5193ms 才给出结果，可见这个的时间差距显著，可以对SUKey进行测信道攻击爆破。

P.S. 如果考虑远程交互过程，如果两个执行时间长度超过 1 秒，那大概率是可以测信道攻击的。但据说之前强网杯那个多项式题不太行，因为时间相差太短了，虽然本地跑是6ms和50ms，但由于网络延迟的存在，这个几十毫秒还是可以忽略的

测试代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from pwn import *
from sage.all import *
from datetime import *

context.log_level = 'debug' #='debug'
ells = [*primes(3, 200), 269]
p = 4*prod(ells) - 1
F = GF(p)
n=len(ells)
sh=process(['sage','task11.sage'])

ts=datetime.now()
C=int(sh.recvline()[4:].strip())
print(datetime.now()-ts)
print(C)

sh.recvuntil(b':')
ts=datetime.now()
sh.sendline(f'{[2]*n}'.encode())
sh.recvuntil(b':')
print(datetime.now()-ts)

ts=datetime.now()
sh.sendline(f'{[4]*n}'.encode())
sh.recvuntil(b':')
print(datetime.now()-ts)

sh.interactive()

16

那么既然知道了这个，就可以开始爆破了，以下是爆破代码

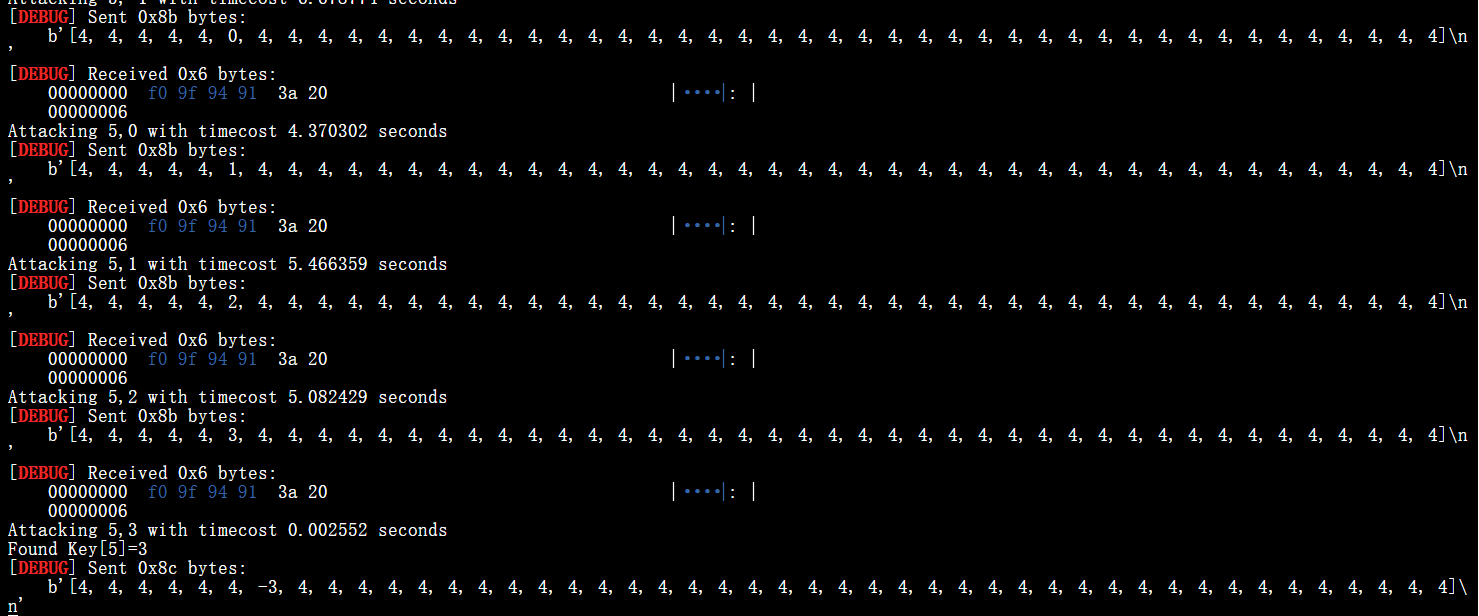
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
from pwn import *
from sage.all import *
from datetime import *

context.log_level = 'debug' #='debug'
ells = [*primes(3, 200), 269]
p = 4*prod(ells) - 1
F = GF(p)
n=len(ells)
sh=process(['sage','task11.sage'])

ts=datetime.now()
C=int(sh.recvline()[4:].strip())
print(datetime.now()-ts)
print(C)

def attack(ind,x):
    #sh.recvline(keepends=False)
    L=[x if (i==ind) else 4 for i in range(n)]
    sh.sendline(str(L).encode())

K=[9]*n
sh.recvuntil(b':')
for i in (range(n)):
    for j in range(-3,4):
        #print(i,j)
        stime=datetime.now()
        attack(i,j)
        sh.recvuntil(b':')
        timecost=(datetime.now()-stime).total_seconds()
        print(f'Attacking {i},{j} with timecost {timecost} seconds')
        if(timecost<0.95):
            K[i]=j
            print(f'Found Key[{i}]={j}')
            print(f'Now, Key is {K}')
            break
print(K)

运行过程中的结果，可以发现这个时间差距非常显著，并且是可以得到最终的Key的。

17

但到这一步又出问题了：我们不知道密文SUDOOR的内容，并且服务器是执行远程的程序才给出的，也就是说，我们需要构造一个KEY，使得构造的KEY和原始私钥的执行结果一样。

由于 $p+1=4\prod_{i=1}^n{\ell_i}$，因此 $\prod_{i=1}^n\ell_i$ 是一个 4-同源，其阶数为 $3$，也就是如果使用全 $1$ 私钥，也就是对于每个 $\ell_i$ 均沿着同源图在上面走一步，那么重复三次就会回到原点——也就是说，同源图点的个数一定是 $3$ 的倍数。

因此，密钥 K1=[3+i for i in K] 与密钥 K 是等价的，因此只需要将所有私钥的值加三，然后发送给服务器就OK了！。

那么最后的攻击代码也就出来了：

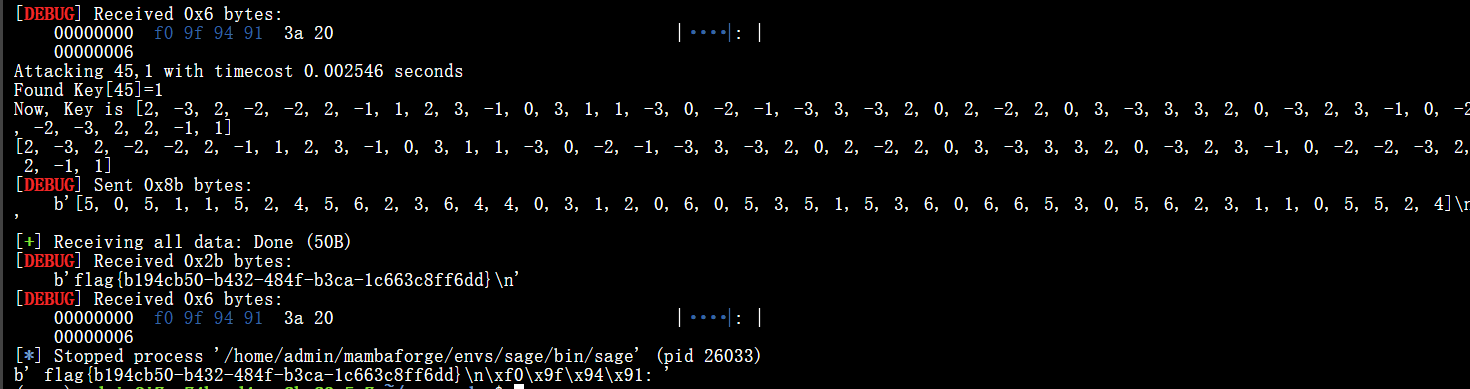
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
from pwn import *
from sage.all import *
from datetime import *

context.log_level = 'debug' #='debug'
ells = [*primes(3, 200), 269]
p = 4*prod(ells) - 1
F = GF(p)
n=len(ells)
sh=process(['sage','task11.sage'])

ts=datetime.now()
C=int(sh.recvline()[4:].strip())
print(datetime.now()-ts)
print(C)

def attack(ind,x):
    #sh.recvline(keepends=False)
    L=[x if (i==ind) else 4 for i in range(n)]
    sh.sendline(str(L).encode())

K=[9]*n
sh.recvuntil(b':')
for i in (range(n)):
    for j in range(-3,4):
        #print(i,j)
        stime=datetime.now()
        attack(i,j)
        sh.recvuntil(b':')
        timecost=(datetime.now()-stime).total_seconds()
        print(f'Attacking {i},{j} with timecost {timecost} seconds')
        if(timecost<0.95):
            K[i]=j
            print(f'Found Key[{i}]={j}')
            print(f'Now, Key is {K}')
            break
print(K)

sh.sendline(f'{[3+i for i in K]}'.encode())     
print(sh.recvall(timeout=5))

本地测试的执行结果（随便写了个flag编译了，因此flag不是原始题目的flag）：18

4.3.2 CSIDH特殊参数的DDH问题

看一个题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
from Crypto.Cipher import AES
from Crypto.Hash import SHA256
from Crypto.Util.Padding import pad

import json
import os

ls = list(primes(3, 112)) + [139]
p = 2 * prod(ls) - 1
max_exp = ceil((sqrt(p) ** (1 / len(ls)) - 1) / 2)
Fp2 = GF(p**2, names="w", modulus=[3, 0, 1])
w = Fp2.gen()
base = EllipticCurve(Fp2, [0, 1])


SECRET = int.from_bytes(os.urandom(8), "big") # 2^64 security is more than enough...
FLAG = b"crypto{????????????????????????????????}"

def encrypt_flag(secret):
    key = SHA256.new(int.to_bytes(int(secret), 8)).digest()[:128]
    iv = os.urandom(16)
    cipher = AES.new(key, AES.MODE_CBC, iv)
    ct = cipher.encrypt(pad(FLAG, 16))

    return iv.hex(), ct.hex()

def private():
    return [randrange(-max_exp, max_exp + 1) for _ in range(len(ls))]

def action(pub, priv):
    E = pub
    es = priv[:]
    while any(es):
        E._order = (p + 1) ** 2  # else sage computes this
        P = E.lift_x(GF(p).random_element())
        s = +1 if P.xy()[1] in GF(p) else -1
        k = prod(l for l, e in zip(ls, es) if sign(e) == s)
        P *= (p + 1) // k
        for i, (l, e) in enumerate(zip(ls, es)):
            if sign(e) != s:
                continue
            Q = k // l * P
            if not Q:
                continue
            Q._order = l  # else sage computes this
            phi = E.isogeny(Q)
            E, P = phi.codomain(), phi(P)
            es[i] -= s
            k //= l
    return E

def backdoor(priv):
    b = 1
    # secret_marks is a redacted CSIDH private key
    for e, m in zip(secret_marks, priv):
        b *= e ^ m
    return b

def package_challenge(EA, EB, EC):
    def package_curve(E):
        return {
            "a4" : list(map(int, E.a4())),
            "a6" : list(map(int, E.a6()))
        }
    return {
        "EA" : package_curve(EA),
        "EB" : package_curve(EB),
        "EC" : package_curve(EC)
    }

def gen_challenge(bit):
    privA = private()
    pubA = action(base, privA)
    privB = private()
    pubB = action(base, privB)
    shared = action(pubB, privA)
    t = backdoor(privA) * backdoor(privB)
    privC = private()
    while backdoor(privC) == t:
        privC = private()
    pubC = action(base, privC)
    if bit:
        return package_challenge(pubA, pubB, shared)
    else:
        return package_challenge(pubA, pubB, pubC)

data = []
for bit in ZZ(SECRET).bits():
    data.append(gen_challenge(bit))

iv, ct = encrypt_flag(SECRET)

output = {}
output["iv"] = iv
output["ct"] = ct
output["challenge_data"] = data 

with open("output.txt", "w") as f:
    f.write(json.dumps(output))

题目的大意很简单：给你三条曲线 $E_A,E_B$ 和 $E_C$，问你 $E_C$ 是 $E_A,E_B$ 复合同源得到的，还是仅仅是随机产生的的曲线，很明显的 DDH 问题的isogeny版本。

注意到这个起始曲线比较特殊：属于 $j(E_0)=0,\sqrt{-3}\in K$ 的特殊曲线，因此无法计算蒙哥马利参数。并且这个题分数还挺高，盲猜是个论文题。

搜了一圈isogeny DDH，可以找到这篇论文：2020-151.pdf，论文第 5 章介绍了几个符号的计算方法，并且参考 18 给出了Github上的magma代码。

由于 $\delta$ 符号的计算比较简单，因此这里可以计算 $\delta(E_B,E_0)$ 和 $\delta(E_A,E_C)$ 是否相等，来判断 $E_C$ 是否是 $E_0$ 经过 $E_A,E_B$ 的复合同源。。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
DATA= #Copy from the output.txt
from Crypto.Cipher import AES
ls = list(primes(3, 112)) + [139]
p = 2 * prod(ls) - 1
max_exp = ceil((sqrt(p) ** (1 / len(ls)) - 1) / 2)
Fp2 = GF(p**2, names="w", modulus=[3, 0, 1])
w = Fp2.gen()
base = EllipticCurve(Fp2, [0, 1])

iv,C=DATA["iv"],DATA["ct"]
D=DATA["challenge_data"]
for i in range(len(D)):
    EA=EllipticCurve(Fp2,[D[i]['EA']['a4'],D[i]['EA']['a6']])
    EB=EllipticCurve(Fp2,[D[i]['EB']['a4'],D[i]['EB']['a6']])
    EC=EllipticCurve(Fp2,[D[i]['EC']['a4'],D[i]['EC']['a6']])
    D[i]=(EA,EB,EC)
PR.<x>=PolynomialRing(GF(p))

def comp(E1,E2):
    f=PR([E1.a6(),E1.a4(),0,1])
    g=PR([E2.a6(),E2.a4(),0,1])
    r=f.roots()[0][0]
    s=g.roots()[0][0]
    judg=GF(p)((E1.a4()+3*r**2)/(E2.a4()+3*s**2))
    return judg**((p-1)//4)==1
M=[comp(D[i][0],D[i][2])==comp(D[i][1],base) for i in range(len(D))]
s=0
for i in range(len(M)):
    s+=(M[i]<<i)
from Crypto.Util.number import *
from hashlib import *
key=sha256(long_to_bytes(s)).digest()
aes=AES.new(key, AES.MODE_CBC, bytes.fromhex(iv))
aes.decrypt(bytes.fromhex(C))

9.总结

真难，好多内容感觉比4年前学LLL的时候还抽象，部分知识其实自己根本就不太懂，但为了速成一波，还是硬着头皮，通过测试代码的方式，用了一个星期（2.1到2.8），对同源有了一个基本理解了。。。等后面遇到题目再推进吧！

CTFSeason4
#Notes
ECCNotes4
http://example.com/2025/02/01/ECCNotes4/
作者
huangx607087
发布于
2025年2月1日
许可协议