25Feb1

huangx607087 2月的切题 1

0.Introduction

近期遇到了几个比较有意思的题目，来看一看！

顺便挂三个令我废透脑筋的题目

1.DASCTF2408-ezSignin

1x01 题目简单分析

先来看一下题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
from Crypto.Util.number import *
from Crypto.Cipher import AES
from secret import flag
import hashlib

p = 174523845247570741054964008585718839267
E = EllipticCurve(GF(p), [0, 486662, 0, 1, 0])
G=E(2247961404505753398791635923994899528, 108711418033303501028455466081133667288)
n=G.order()
Cofactor = E.order() // n
f = 128+1
lambda_ = 100

def retbar(P):
    index = (f + 1) // 2
    return (int(P[0]) % (2 ^ index) + 2 ^ index) % n

def genkey():
    w = randint(1, n - 1)
    W = w * G
    return (w, W)

B_pri_w, B_pub_W = genkey()
print(B_pub_W[0:2])

LS = []
LR = []
BR = []

def Exchange(i):
    A_pri_w, A_pub_W = genkey()
    A_pri_r, A_pub_R = genkey()
    B_pri_r, B_pub_R = genkey()

    sa = (A_pri_r + retbar(A_pub_R) * A_pri_w) % n
    sb = (B_pri_r + retbar(B_pub_R) * B_pri_w) % n

    Ka = Cofactor * (B_pub_R + retbar(B_pub_R) * B_pub_W) * sa
    Kb = Cofactor * (A_pub_R + retbar(A_pub_R) * A_pub_W) * sb

    assert (Ka == Kb)

    leakageS = sb >> lambda_
    leakageR = B_pri_r >> lambda_

    LS.append(leakageS), LR.append(leakageR)
    BR.append(B_pub_R[0:2])

for i in range(10): Exchange(i)
    
print("LS=", LS)
print("LR=", LR)
print("BR=", BR)
H=hashlib.md5()
H.update(long_to_bytes(B_pri_w))
key=H.hexdigest().encode()
aes = AES.new(key,AES.MODE_ECB)
print(aes.encrypt(flag))

乍一看，是一个之前做烂掉的ECDH的密钥交换协议，题目给出了 B 的公钥 $xG$，每一次密钥交换的 sb,B_pri_r 的高位，以及完整的 B_pub_R 的点，并且这边的线性关系式也很简单，$B_{pub,r}$ 给出后，$f(B_{pub,r})$ 也下能当与作为定值给出了。
$$
s_B=B_{pri,r}+f(B_{pub,r})w_B
$$
为了方便展示，我们设 LS,LR,BR 分别记为为 $S,R,P$，其中 $S_{i}=2^{100}s_i+x_i,R_i=2^{100}r_i+y_i$，B 的固定私钥为 $w$。但实际上，LS,LR 中存放的其实是 $s_i$ 和 $r_i$，$x_i$ 和 $y_i$ 是右移被省略的内容。

那么上面的等式就可以写为：
$$
2^{100}s_i+x_i\equiv 2^{100}r_i+y_i-f(P)w \pmod n
$$
整理一下：
$$
x_i-y_i=2^{100}(r_i-s_i)-f(P_i)w-k_in
$$
如果把 $x_i-y_i$ 当作整体，那就是：
$$
z_i=2^{100}(r_i-s_i)-f(P_i)w-k_in
$$
设 $A_i=r_i-s_i,B_i=f(P_i)$，逻辑就出来了：
$$
z_i=2^{100}A_i-wB_i-k_in
$$
所以构造矩阵如下：

1

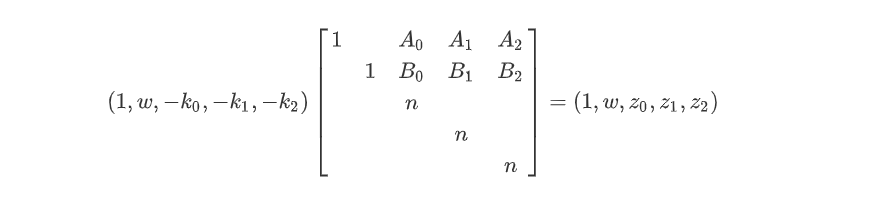
由于 $w$ 是 $128$ 位，$z$ 是 $100$ 位，那么需要乘平衡系数为 $\mathrm{diag}(2^{128},1,2^{28},2^{28},2^{28})$，然后LLL求解。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from Crypto.Util.number import *
from Crypto.Cipher import AES
import hashlib

p = 174523845247570741054964008585718839267
E = EllipticCurve(GF(p), [0, 486662, 0, 1, 0])
G=E(2247961404505753398791635923994899528, 108711418033303501028455466081133667288)
n=G.order()
H=E(56142839234500040174315077324489019612, 143186177525574678948140963663687495447)
LS= [12160779, 70634852, 136488679, 93279448, 51769705, 99408367, 94011238, 46255543, 136054320, 126842658]
LR= [117789932, 85602320, 136131278, 85538539, 33115646, 15821127, 122073977, 40205177, 40509142, 121833940]
BR= [(43128875586771925869851532015581155657, 108714366549720544283054523544596695631), (166053844834143846221197595138208659402, 9389299139547698081250285594708260233), (83160043610860066750778648875060399604, 160655466348101518011620435983302563358), (18306927902958362110653472691194540502, 141566997533915037448387258113883793369), (124719869188706449552550102421264489653, 111266021208672789646176095367638959348), (62115794167524204331339724293036031704, 24476842210910012261000793337134128911), (57017187772347635647835418540384524017, 149273114828279413180900590599119201032), (141865913804035015431129030802262884043, 11219445710980991629921733217597739715), (35994282847505215202392163277052083355, 5366425669461724819918825109516828913), (72621299937996657982583201267406651177, 39297013522202608324989011761142875947)]
C=b'\xd7\x8c\xf1Yx\x05W\x8ckq\xfdb\xd5\x81K"\xe7q\x88\x18\xedq\x9f\xcap\x1cTB\xc9)\xe1c\xf4~\x7f\xccwh\xfe\t\xbf\xb2!\xde\x84\xeeO\x0f8\xd1\xac\xbc\x1c \xf0F\x0c\x00\xc9\xa7\x9e\x06\xdan'
def retbar(P):
    index = 130//2
    return (int(P[0]) % (2 ** index) + 2 ** index) % n
A=[2**100*(LS[i]-LR[i]) for i in range(10)]
B=[-retbar(BR[i]) for i in range(10)]
M=block_matrix([
    [identity_matrix(2),matrix([A,B])],
    [zero_matrix(10,2),n*identity_matrix(10)]
])
B=diagonal_matrix([2**128,1]+[2**28]*10)
M3L=((M*B).LLL())*(B**-1)
vec=None
for vec in M3L:
    if(abs(vec[0])==1):
        break
x=int(vec[0]*vec[1])
print('{:032x}'.format(x))
#00e2e6517a7ca4a6fdeeacca2fa34781

这么做貌似确实没有什么问题，我们得到的参数的数量级也对，检查了一下行列式的值，也基本符合要求。但尝试用解出来的 $w$ 解密flag，竟然不对？！

1x02 给 $wG$ 的作用

注意到题目给出了 $wG$ 的值，这个值我们还没有用到。

不管了，测一下它的代码，果然，发现了玄机：最终解出来的 $w$ 和实际的 $w_B$ 有 $±2^{33}$ 数量级的误差，这就导致目标向量其实并不是我们解出来的最短向量。（这个测试的代码可以自己写一个，这个题我是2月1日做的，测试的代码丢了就不发了，自己运行它题目中的代码，输出 $w_B$，再运行上面的解题代码，计算那两个值的差就OK）。

换句话说，$w_B$ 的低 $34$ 位我们不知道，这个值直接枚举太大了，考虑对未知部分进行bsgs，这样才能得到flag。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
xbar=(x>>34)<<34
K=H-xbar*G
D=dict()
from tqdm import *
P=E(0)
G2=G*2**17
for i in tqdm(range(2**17)):
    D[P]=i
    P=P+G2
P=E(0)
Ktmp=K
for i in tqdm(range(2**17)):
    u=D.get(Ktmp,None)
    if(u):
        v=i
        print(u,v)
        break
    Ktmp-=G
x=xbar+(u<<17)+v
print('{:032x}'.format(xbar))
print('{:032x}'.format(x))
#60999 17385
#00e2e6517a7ca4a6fdeeacc800000000
#00e2e6517a7ca4a6fdeeacc9dc8e43e9
from hashlib import md5
key=md5(long_to_bytes(x)).hexdigest().encode()
aes = AES.new(key,AES.MODE_ECB)
print(aes.decrypt(C))
#b'DASCTF{C0ngRatul4tion5_On_y0ur_SuCc3ssfuL_S1gN_1n}'

看来有的时候测一下题目代码还是有必要的:)，签个到还真不容易呢。。。

2.[VNCTF2025]sh1kaku_fw

2x01 题目代码

又是一个LWE的题目，来看一下代码！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
from Crypto.Util.number import getPrime 
from sympy import nextprime
import numpy as np
import random
import signal
import os


def _handle_timeout(signum, frame):
    raise TimeoutError('function timeout')

timeout = 450
signal.signal(signal.SIGALRM, _handle_timeout)
signal.alarm(timeout)

def uniform_sample(n, bound, SecureRandom):
    return [SecureRandom.randrange(-bound, bound) for _ in range(n)]

def choice_sample(n, L, SecureRandom):
    return [SecureRandom.choice(L) for i in range(n)]

n = 197
m = 19700
q = getPrime(20)

e_L = [random.randrange(0, q-1) for i in range(2)]
R_s = random.SystemRandom()
R_e = random.SystemRandom()

s = np.array(uniform_sample(n, q//2, R_s))
e = np.array(choice_sample(m,  e_L, R_e))

seed = os.urandom(16)
R_A = random
R_A.seed(seed)
A = np.array([uniform_sample(n, q, R_A) for _ in range(m)])
b = (A.dot(s) + e) % q

print(f"{q = }")
print(f"{e_L = }")
print(f"{seed.hex() = }")
print(f"{b.tolist() = }") 
s_ = input("Give me s: ")
from datetime import *
if s_ == str(s.tolist()):
    print("Congratulations! You have signed in successfully.")
    print(('flag{success at_'+str(datetime.now())+'}').replace(' ','_'))
else:
    print("Sorry, you cannot sign in.")

2x02 题目分析

可以看到题目中给出了一个 $197\times19700$ 的矩阵 $A$，模数 $q$，目标向量 $\vec b$ 和 误差 $e$ 可能的取值。

对于 $A\cdot \vec s+\vec e=b$，如果把矩阵 $A$ 拆成 $19700$ 个行向量，那么每个行向量都有 $\vec a_i\cdot \vec s+e_i=b$，也就是 $b-\vec a_i\cdot \vec s-e_i=0$。

由于 $e_i$ 只有两种取值 $e_1,e_2$，那么必定有 $b-\vec a_i\cdot \vec s-e_1=0$ 或者 $b-\vec a_i\cdot \vec s-e_2=0$。既然两个成立一个，那乘起来就一定有
$$
(b-\vec a_i\cdot \vec s-e_1)(b-\vec a_i\cdot \vec s-e_2)=0
$$
这个方法在25Jan1中解NTRU时也用到过。

既然这样，那么我们要做的就是展开 $\vec a_i\cdot \vec s$，然后这里可以构成一个关于 $s_0,s_1,…s_{196}$ 的多项式。由于是两个相乘，那就会有 $197$ 个一次项 $s_0\sim s_{196}$，$197$ 个平方项 $s_0^2\sim s_{196}^2$ 以及 $197\times98$ 个交叉项 $s_0s_1,…,s_{195}s_{196}$，共 $19700$ 项，将这些变量线性化，看作 $19700$ 个一次的未知数，那我们刚好可以利用题目给出的条件，构造 $19700$ 个线性方程组解这 $19700$ 个未知数。

根据推导，方程左边构造的对应的系数如下：

未知数 系数
$s_i,\space0\le i\lt197$ $F_i=-2ba_i+(e_1+e_2)a_i-e_1e_2$
$s_i^2,\space0\le i\lt197$ $G_i=a_i^2$
$s_is_j,\space0\le i\lt j\lt197$ $H_{(i,j)}=2a_ia_j$

而方程的右边，就是没有 $s$ 的部分，那就是 $-b^2+b(e_1+e_2)-e_1e_2$。

这样，对于 $A$ 中的每个行向量，都可以构造一个这样的线性方程组：
$$
\sum_{i=0}^{196}\left(F_is_i\right)+\sum_{i=0}^{196}\left(G_is_i^2\right)+\sum_{i=0}^{195}\sum_{j=i+1}^{196}\left(H_{(i,j)}s_is_j\right)\equiv -b^2+b(e_1+e_2)-e_1e_2\pmod q
$$

2x03 解题细节

因为分析过程自己已经接触过，所以这一步很顺利，但为了保证正确性，先写个代码测一下：

数据生成代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
from Crypto.Util.number import getPrime 
from sympy import nextprime
import numpy as np
import random
import signal
import os
def uniform_sample(n, bound, SecureRandom):
    return [SecureRandom.randrange(-bound, bound) for _ in range(n)]

def choice_sample(n, L, SecureRandom):
    return [SecureRandom.choice(L) for i in range(n)]

n = 8
#n=45
#n = 197
m = 2*n+((n-1)*n)//2
q = getPrime(20)

e_L = [random.randrange(0, q-1) for i in range(2)]
R_s = random.SystemRandom()
R_e = random.SystemRandom()

s = np.array(uniform_sample(n, q//2, R_s))
e = np.array(choice_sample(m,  e_L, R_e))

seed = os.urandom(16)
R_A = random
R_A.seed(seed)
A = np.array([uniform_sample(n, q, R_A) for _ in range(m)])
b = (A.dot(s) + e) % q

print(f"{q = }")
print(f"{e_L = }")
print(f"{seed.hex() = }")
print(f"{b.tolist() = }") 
print(f"{s.tolist() =}")

测试代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
import random
import numpy as np
from Crypto.Util.number import *
def uniform_sample(n, bound, SecureRandom):
    return [SecureRandom.randrange(-bound, bound) for _ in range(n)]

n = 8
# n = 197
m = 2*n+((n-1)*n)//2

q = 608383
eL = [98779, 155323]
seed = 0x73d8484f0895b86fc626b3d2a7c9ebd4
b = [28366, 263794, 516785, 140422, 94800, 135315, 574033, 522331, 292172, 341996, 601981, 546391, 85872, 492583, 30138, 3278, 301462, 411086, 151442, 247950, 580873, 468430, 132926, 247908, 174415, 465168, 382582, 16723, 540657, 158201, 259050, 350638, 193228, 521987, 429135, 554774, 273844, 281732, 591536, 267711, 605959, 582472, 491069, 140874]
s_debug =[-63716, -295937, 294401, 183923, 36465, 241521, -43816, 217716]
R_A = random
R_A.seed(long_to_bytes(seed))
A = np.array([uniform_sample(n, q, R_A) for _ in range(m)]).tolist()
A=Matrix(GF(q),A)
vecb=vector(GF(q),b)
from tqdm import *
from datetime import *
STIME=datetime.now()
print(str(STIME))
M=[]
y=[]
e1,e2=eL
for i in tqdm_notebook(range(m)):
    veca=A[i]
    bi=vecb[i]
    y.append(bi*bi-bi*(e1+e2)+e1*e2)
    vecline=[]
    for j in range(n):
        vecline.append(2*bi*A[i][j]-(e1+e2)*A[i][j])
    for j in range(n):
        vecline.append(A[i][j]**2)
    for j in range(n):
        for k in range(j+1,n):
            vecline.append(-2*A[i][j]*A[i][k])
    M.append(vecline)
M=Matrix(GF(q),M)
y=vector(GF(q),y)
ans=M.solve_right(y)
s=(ans[:n])
s_debug=vector(GF(q),s_debug)
print(s)
print(s==s_debug)
TTIME=datetime.now()
print(str(TTIME))
print(TTIME-STIME)
"""
(544667, 312446, 294401, 183923, 36465, 241521, 564567, 217716)
True
2025-02-18 22:04:57.003973
0:00:00.489371
"""

在本机测了一组 $n=8$ 和 $n=20$ 都没有问题，看来算法是对的。那就直接上 $n=197$，但这真是炸裂的存在啊！

2

因为自己windows用的是sage9.3，不妨在虚拟机上跑sage10.4：也就快了一丢丢而已。。。

2b

然后自己问了下出题人dbt，最后一句话引起了我注意：

1
2
3
4
5
6
7
8
9
10
11
12
huangx607087 2025/2/10 17:47:06
那个题建矩阵用的啥版本sage？

crypto-fwshikaku 2025/2/10 17:49:51
你这复杂度吓人

crypto-fwshikaku 2025/2/10 17:50:06
10.5我感觉版本关系不大啊

crypto-fwshikaku 2025/2/10 17:50:12
就python内置list啊

终于，罪魁祸首找到了，原来sage模 $q$ 有限域太慢了！：

1
2
3
4
5
6
R_A = random
R_A.seed(long_to_bytes(seed))
A = np.array([uniform_sample(n, q, R_A) for _ in range(m)]).tolist()
#A=Matrix(GF(q),A)  #deleted
#vecb=vector(GF(q),b) #deleted
vecb=b.copy() #new added

速度果然快起来了，并且快了50倍，好家伙。。。

2c

然而这么做爆内存了（虚拟机内存已经被我调到了 16GB），现在打CTF没高配还不行了是吧，是不是下一台电脑得买 64G 的了？

2d

原来一个int在python中占28字节，那还得再优化一下，用numpy优化成 4 字节，这样内存爆得总算不那么夸张了。。。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
M=np.zeros((19700,19700),dtype=np.int32)
y=[0]*m
e1,e2=eL
for i in tqdm(range(m)):
    veca=A[i]
    bi=vecb[i]
    y[i]=(bi*bi-bi*(e1+e2)+e1*e2)%q
    cur=0
    for j in range(n):
        M[i][cur]=(2*bi*A[i][j]-(e1+e2)*A[i][j])%q
        cur+=1
    for j in range(n):
        M[i][cur]=(A[i][j]**2)%q
        cur+=1
    for j in range(n):
        for k in range(j+1,n):
            M[i][cur]=(-2*A[i][j]*A[i][k])%q
            cur+=1

不过这个在本地测试的时候，还是跑了 15 分钟，时间还是有点偏长了，原题只有7.5分钟，但解方程组作为正解，这还真不好简化掉。

3

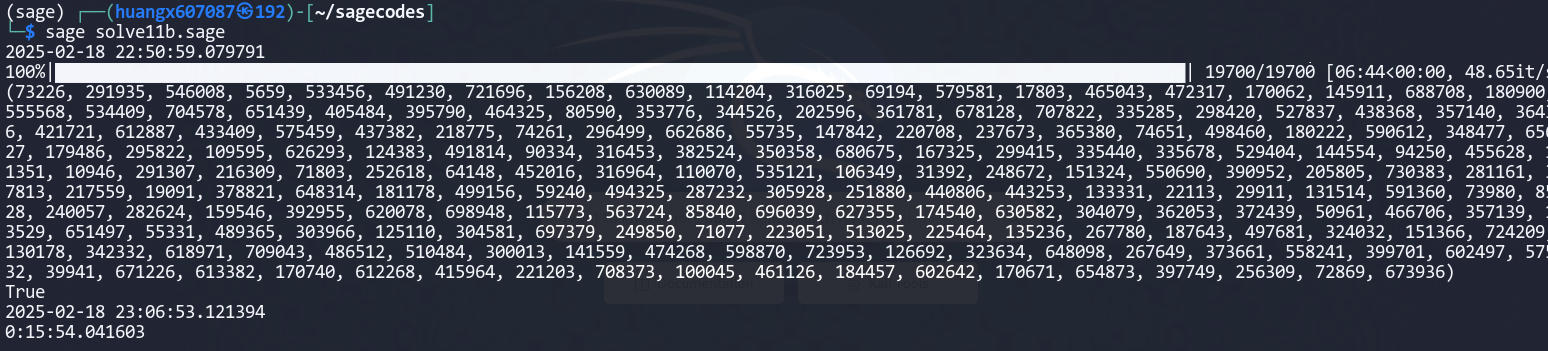
注意到这里构造矩阵用了 7 分钟，考虑多进程加速：开 4 个进程同步写数据构造矩阵，这样构造矩阵的时间就缩短到了 2 分 20 秒。，耗时大概十二分半，那么我们还有三分钟时间接收和发送数据。由于这个题的交互量不大，因此这个时间也算是够了。

2x04 exp

最终完成的代码如下，4进程耗时 13 分钟，本地把时间调成了 900 秒做的，实在想不出还有什么优化方法了。。。（也看不到出题人的exp）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
import random
import numpy as np
from Crypto.Util.number import *
from datetime import *
from pwn import *
def uniform_sample(n, bound, SecureRandom):
    return [SecureRandom.randrange(-bound, bound) for _ in range(n)]

n = 197
m = 2*n+((n-1)*n)//2
print(m%4)
sh=process(['sage','sh1kaku_fw_server.sage'])
sh.recvuntil(b'=')
q = eval(sh.recvline(keepends=False))
sh.recvuntil(b'=')
eL = eval(sh.recvline(keepends=False))
sh.recvuntil(b'=')
seed=eval(sh.recvline(keepends=False))
sh.recvuntil(b'=')
b=eval(sh.recvline(keepends=False))
# sh.recvuntil(b'=')
# s_debug=eval(sh.recvline(keepends=False))
R_A = random
R_A.seed(bytes.fromhex(seed))
A = np.array([uniform_sample(n, q, R_A) for _ in range(m)]).tolist()
vecb=b.copy()
e1,e2=eL
import numpy as np
import multiprocessing as mp
from multiprocessing.shared_memory import SharedMemory
from tqdm import *
print(datetime.now())
def write_to_k(start_row, end_row, shm_name, shm_name2,shape,shape2, dtype):
    # 连接到共享内存
    existing_shm = SharedMemory(name=shm_name)
    existing_shm2 = SharedMemory(name=shm_name2)
    K = np.ndarray(shape, dtype=dtype, buffer=existing_shm.buf)
    B = np.ndarray(shape2, dtype=dtype, buffer=existing_shm2.buf)
    for i in tqdm_notebook(range(start_row,end_row)):
        bi=vecb[i]
        B[i]=(-bi*bi+bi*(e1+e2)-e1*e2)%q
        cur=0
        for j in range(n):
            K[i][cur]=(-2*bi*A[i][j]+(e1+e2)*A[i][j])%q
            cur+=1
        for j in range(n):
            K[i][cur]=(A[i][j]**2)%q
            cur+=1
        for j in range(n):
            for k in range(j+1,n):
                K[i][cur]=(2*A[i][j]*A[i][k])%q
                cur+=1
    existing_shm.close() 


# m=19700
num_processes = 4
rows_per_process = m//4
shape = (m, m)
shape2= (m)
dtype = np.int32

# 创建共享内存
shm = SharedMemory(create=True, size=np.prod(shape) * np.dtype(dtype).itemsize)
shm2 = SharedMemory(create=True, size=np.prod(shape2) * np.dtype(dtype).itemsize)
K = np.ndarray(shape, dtype=dtype, buffer=shm.buf)
B = np.ndarray(shape2,dtype=dtype, buffer=shm2.buf)
processes = []

for i in range(num_processes):
    start_row = i * rows_per_process
    end_row = start_row + rows_per_process
    p = mp.Process(target=write_to_k, args=(start_row, end_row, shm.name,shm2.name , shape, shape2, dtype))
    processes.append(p)
    p.start()

for p in processes:
    p.join()
print(datetime.now())

# K=Matrix(GF(q),K)
M=Matrix(GF(q),K)
y=vector(GF(q),B)
print(datetime.now())
ans=M.solve_right(y)
print(datetime.now())
s2=(ans[:n])
# s_debug=vector(GF(q),s_debug)
print(s2)
print(datetime.now())
sh.recvuntil(b':')
s=[Integer(s2[i]) if s2[i]<(q//2) else Integer(s2[i])-Integer(q) for i in range(len(s2))]
sh.sendline(str(s).encode())
print(sh.recvall(timeout=8).decode())
print(datetime.now())
"""

[x] Starting local process '/home/huangx607087/mambaforge/envs/sage/bin/sage'
[+] Starting local process '/home/huangx607087/mambaforge/envs/sage/bin/sage': pid 264101
2025-02-19 09:15:47.298775
2025-02-19 09:18:24.058344
2025-02-19 09:22:58.562647
2025-02-19 09:27:38.079743
(413089, 182407, 281293, 514536, 416848, 162144, 111292, 567942, 105638, 320217, 597752, 148614, 475740, 104923, 168548, 419776, 331148, 480665, 27938, 144285, 536717, 23041, 407741, 535865, 292620, 296206, 263837, 411101, 178021, 459126, 582200, 356604, 260864, 107465, 198975, 603533, 614391, 399204, 281846, 656596, 336371, 43032, 469948, 485132, 292949, 551266, 481705, 627344, 294383, 16843, 351274, 499494, 400866, 16300, 397952, 418611, 329186, 171588, 126742, 35187, 227634, 47279, 558263, 274274, 176943, 213254, 136124, 458182, 207387, 110241, 561213, 643075, 37905, 81904, 541660, 591129, 252387, 442913, 59602, 291489, 16114, 33889, 42797, 178984, 170978, 125577, 44397, 84513, 42300, 190430, 131960, 171794, 438727, 575807, 132652, 483489, 537433, 148391, 295287, 611719, 433771, 511639, 429386, 96772, 149829, 391049, 203110, 134839, 614783, 116974, 563429, 625857, 583438, 296242, 287114, 567163, 311443, 300000, 319030, 157568, 340472, 574056, 58440, 504748, 659358, 158919, 513009, 450907, 372321, 505831, 160026, 450642, 598087, 385168, 351908, 608844, 282572, 345722, 528174, 464689, 476965, 642386, 235728, 498266, 341476, 84067, 177778, 590226, 41793, 286838, 98328, 123973, 354428, 101602, 362267, 6228, 519006, 43713, 314830, 37731, 479235, 46098, 147882, 455284, 472502, 508348, 408861, 509481, 50884, 609377, 5300, 625054, 139267, 436879, 7235, 344990, 388357, 645294, 314985, 497667, 663837, 527331, 13209, 457430, 574164, 460940, 171654, 38269, 124149, 583682, 216156, 356979, 571283, 665300, 411729, 172241, 320462)
2025-02-19 09:27:38.080569
[x] Receiving all data
[x] Receiving all data: 1B
[x] Receiving all data: 95B
[+] Receiving all data: Done (95B)
[*] Process '/home/huangx607087/mambaforge/envs/sage/bin/sage' stopped with exit code 0 (pid 264101)
 Congratulations! You have signed in successfully.
flag{success_at_2025-02-19_09:27:38.082088}
2025-02-19 09:27:38.292391
"""

3.[N1CTF_junior]StrangeCurve

3x01 题目代码

先看一眼题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
import os
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from hashlib import sha256
from uuid import *
from datetime import *
FLAG = 'flag{'+str(uuid4())+'}'
if isinstance(FLAG, str):
    FLAG = FLAG.encode()
# print(FLAG)
ells = [*primes(3, 102)] + [149]
mxe = 6
p = 4 * prod(ells) - 1
Fp = GF(p)
Fp2 = GF(p ** 2)
base = EllipticCurve(Fp2, [0, 0, 0, 1, 0])
privkey = [randint(0, mxe) for _ in ells]

with open('testans'+(str(datetime.now())[11:-7]),'w') as f:
    f.write(str(FLAG)+'\n')
    f.write(str(privkey))
def to_montgomery(E: EllipticCurve) -> int:
    Ep = E.change_ring(Fp).short_weierstrass_model()
    a, b = Fp(Ep.a4()), Fp(Ep.a6())
    P.<x> = PolynomialRing(Fp)
    r = (x^3 + a*x + b).roots()[0][0]
    s = sqrt(3 * r^2 + a)
    if not is_square(s):
        s = -s
    A = 3 * r / s
    return int(Fp(A))

def action(key: list, r: int) -> EllipticCurve:
    E = base
    round = 0
    while any(key):
        E._order = (p + 1) ** 2
        k = prod([l for l, e in zip(ells, key) if e > 0])
        while True:
            P = E.lift_x(Fp.random_element())
            if randint(0, round == r) != (P.xy()[1] in Fp):
                break
        P *= (p + 1) // k
        for i, (l, e) in enumerate(zip(ells, key)):
            if e == 0:
                continue
            Q = k // l * P
            if not Q:
                continue
            Q._order = l
            phi = E.isogeny(Q)
            E, P = phi.codomain(), phi(P)
            key[i] -= 1
            k //= l
        round += 1
    return E

key = sha256(str(privkey).encode()).digest()
cipher = AES.new(key = key, mode = AES.MODE_ECB)
ct = cipher.encrypt(pad(FLAG, 16))
print(f"This is your flag: {ct.hex()}")

while True:
    r = int(input("Get your Curve >").strip())
    assert 0 <= r < 16
    E = action(privkey.copy(), r)
    print(hex(to_montgomery(E)))

3x02 题目分析

这个题目实现的是CSIDH的过程，但对CSIDH做了改动，我们注意action函数中的这一部分：

1
2
3
4
while True:
    P = E.lift_x(Fp.random_element())
    if randint(0, round == r) != (P.xy()[1] in Fp):
        break

我们会发现，在第round轮中，有一半概率使得CISDH中取的 $P$ 点的 $y$ 值在 $\mathbb F_{p^2}$ 而不是 $\mathbb F_{p}$ 上，回顾刚学过的 CISDH，这会导致在第round轮同源的方向变为原来的反方向。如果原来的密钥为 $[3,0,3,2,1,4]$，那么理想情况下，密钥的变化应当为：

1
2
3
4
5
round 0:[+,0,+,+,+,+]
round 1:[+,0,+,+,0,+]
round 2:[+,0,+,0,0,+]
round 3:[0,0,0,0,0,+]
sum:    [3,0,3,2,1,4]

假设round=2时发生了翻转，那么实际情况就是

1
2
3
4
5
round 0:[+,0,+,+,+,+]
round 1:[+,0,+,+,0,+]
round 2:[-,0,-,0,0,-]
round 3:[0,0,0,0,0,+]
sum:    [1,0,1,2,1,2]

也就是说，如果发生翻转，那么第 $2$ 轮中，所有密钥值大于 $2$ 的私钥分量都会逆着走一步，这样和正确的密钥就相差了 $2$ 步。用更加严谨的说法就是：设正确的共享值为 $V$，那么第 $k$ 轮若发生翻转，则最终的共享值为 $[(\prod_{e_i>k}\ell_i)^{-2}]V$ 。

但我们需要注意一个问题，由于在CSIDH中，对于不同的 $\ell$，$P$ 是随机取一个阶为 $\ell$ 的电脑点，因此对于每个 $\ell$，均有 $1/\ell$ 的概率取到无穷远点 $\mathcal O$，这就会导致这一轮提前结束，但不会影响到最终结果（在 $\ell$ 较小的时候该情况出现较多）。

1
2
3
4
5
6
7
P *= (p + 1) // k
for i, (l, e) in enumerate(zip(ells, key)):
    if e == 0:
        continue
    Q = k // l * P
    if not Q:
        continue

这个过程也可以用下面的示意图表示，虽然最终结果一样，但轮数多了 1 轮。不过这种错误可以用多次取样规避。

1
2
3
4
5
6
7
round 0:[+,0,+,+,+,+]
round 1:[+,0,+,+,0,+]
round 2:[+,0,0,0,0,0]
not Q,contiune!
round 3:[0,0,+,0,0,+]
round 4:[0,0,0,0,0,+]
sum:    [3,0,3,2,1,4]

但就算出现上面这种情况，由于私钥的最大值为 $6$，而题目允许输入的最大值为 $15$。经过测试发现，round的值几乎不会超过 $11$，因此可以先发送 $15$，获取正确的共享秘密值 （也就是蒙哥马利参数 $a_{15}$），然后多次测试 $5,4,3,2,1,0$，取次最大概率（因为最大概率是 $a_{15}$，该概率占到一半，测了一下，取样 $600$ 次基本就可以得到理想状态下的 $a_5,…,a_0$ 值）。

然后看了一下 出题人的博客，他给出的做法是MITM，也就是中间相遇攻击，但没有给出进一步的细节。然后我就以为是从 $a_{15},a_{5},a_{4},a_{3}$ 走一个过程，然后再从 $a_{0},a_1,a_2,a_3$ 走一个过程，找相同的 $a_3$。考虑到私钥是 $0\sim6$ 的取值，且私钥长度为 $26$，因此可以赌每个值出现次数不超过 $5$，每一轮需要枚举 $83000$ 多次，耗时三小时，即使开四进程也要 40 分钟一轮，$1000$ 次的成功概率约为 $180$ 次。

3x03 正确做法

然后我问了一下出题人，结果发现是从 $a_{15}$ 出发，每次分别只考虑一个值。在理想情况下，设 $e=[6,0,6,2,5,4,6,3]$，那么我们有：
$$
a_{5}=[-2,0,-2,0,0,0,-2,0]a_{15}
$$
我们可以对半找一个中间值 $a_{5,15}$，满足：
$$
a_{5,15}=[-2,0,-2,0,0,0,0,0]
$$
这样，从 $a_{15}$ 去逆推 $a_{5,15}$，只需要考虑后半部分，从 $a_5$ 去正推 $a_{5,15}$，只需要去推前半部分，两边枚举的复杂度就会降低到原来的一半。

可以直接利用他的action，把round设置成9999去正推。而逆推根据CSIDH的加三等价性，也就是 [3+i for i in privkey] ，那么可以把不需要逆推的部分设置成3，需要逆推的部分设置成1。对应代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
def action(key: list, r: int,ma2:int) -> EllipticCurve:
    E = EllipticCurve(Fp2,[0,ma2,0,1,0])
    round = 0
    while any(key):
        E._order = (p + 1) ** 2
        k = prod([l for l, e in zip(ells, key) if e > 0])
        while True:
            P = E.lift_x(Fp.random_element())
            if randint(0, round == r) != (P.xy()[1] in Fp):
                break
        P *= (p + 1) // k
        for i, (l, e) in enumerate(zip(ells, key)):
            if e == 0:
                continue
            Q = k // l * P
            if not Q:
                continue
            Q._order = l
            phi = E.isogeny(Q,algorithm='factored')
            E, P = phi.codomain(), phi(P)
            key[i] -= 1
            k //= l
        round += 1
    return E
for ai in [a5,a4,a3,a2,a1,a0]:
    print('Timestamp K:',str(datetime.now()))
    D=dict()
    for i in tqdm(range(1,2**13)):
        priv=[2*bool(i&(1<<j)) for j in range(13)]+[0]*13
        Et=action(priv.copy(),9999,ai)
        x=to_montgomery(Et)
        D[x]=i
    for i in tqdm(range(1,2**13)):
        priv=[3]*13+[3-2*(bool(i&(1<<j))) for j in range(13)]
        Et=action(priv.copy(),9999,a15)
        at=to_montgomery(Et)
        x=D.get(at,0)+D.get(p-at,0)
        if(x):
            print(i,x)
            break

但这样第二个步骤会走得很慢。因为priv中有很多 $3$，意味着程序至少要走三轮。

所以可以把action这么改，这样就反过来走了：

1
2
3
4
5
6
7
8
9
10
11
12
def actioninv(key: list, r: int,ma2:int) -> EllipticCurve:
    E = EllipticCurve(Fp2,[0,ma2,0,1,0])
    round = 0
    while any(key):
        E._order = (p + 1) ** 2
        k = prod([l for l, e in zip(ells, key) if e > 0])
        while True:
            P = E.lift_x(Fp.random_element())
            if randint(1,1) != (P.xy()[1] in Fp): #changed!
                break
        P *= (p + 1) // k
        #complete the same as action below.

3x04 exp

3.4.1 初步exp

根据3x03的分析，初步给出exp。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
from pwn import *
from Crypto.Util.number import *
from tqdm import *
from sage.all import *
from datetime import *
print('Timestamp 1:',str(datetime.now()))
sh=process(['sage','task16.sage'])
sh.recvuntil(b':')
ciph=sh.recvline(keepends=False).strip()
print(ciph)

def get(x,tmz):        
    D=[]
    for i in tqdm(range(tmz)):
        sh.recvuntil(b'>')
        sh.sendline(str(x).encode())
        res=sh.recvline(keepends=False).decode()
        D.append(eval(res))
    def cmp(arg):
        return -arg[1]
    R=sorted([(i,D.count(i)) for i in set(D)],key=cmp)
    return R
D15=get(15,50)
D5=get(5,600)
D4=get(4,600)
D3=get(3,600)
D2=get(2,600)
D1=get(1,600)
D0=get(0,600)
print('Timestamp 2:',str(datetime.now()))

sh.close()
a15=D15[0][0]
a5,a4,a3,a2,a1,a0=[arr[1][0] for arr in [D5,D4,D3,D2,D1,D0]]
print(f'{a15=}')
print(f'{a5=}')
print(f'{a4=}')
print(f'{a3=}')
print(f'{a2=}')
print(f'{a1=}')
print(f'{a0=}')
ells = [*primes(3, 102)] + [149]
p = 4 * prod(ells) - 1
Fp=GF(p)
Fp2=GF(p**2)
def to_montgomery(E: EllipticCurve) -> int:
    Ep = E.change_ring(Fp).short_weierstrass_model()
    a, b = Fp(Ep.a4()), Fp(Ep.a6())
    P.<x> = PolynomialRing(Fp)
    r = (x^3 + a*x + b).roots()[0][0]
    s = sqrt(3 * r^2 + a)
    if not is_square(s):
        s = -s
    A = 3 * r / s
    return int(Fp(A))

def action(key: list, r: int,ma2:int) -> EllipticCurve:
    E = EllipticCurve(Fp2,[0,ma2,0,1,0])
    round = 0
    while any(key):
        E._order = (p + 1) ** 2
        k = prod([l for l, e in zip(ells, key) if e > 0])
        while True:
            P = E.lift_x(Fp.random_element())
            if randint(0, round == r) != (P.xy()[1] in Fp):
                break
        P *= (p + 1) // k
        for i, (l, e) in enumerate(zip(ells, key)):
            if e == 0:
                continue
            Q = k // l * P
            if not Q:
                continue
            Q._order = l
            phi = E.isogeny(Q,algorithm='factored')
            E, P = phi.codomain(), phi(P)
            key[i] -= 1
            k //= l
        round += 1
    return E
def actioninv(key: list, r: int,ma2:int) -> EllipticCurve:
    E = EllipticCurve(Fp2,[0,ma2,0,1,0])
    round = 0
    while any(key):
        E._order = (p + 1) ** 2
        k = prod([l for l, e in zip(ells, key) if e > 0])
        while True:
            P = E.lift_x(Fp.random_element())
            if randint(1,1) != (P.xy()[1] in Fp):
                break
        P *= (p + 1) // k
        for i, (l, e) in enumerate(zip(ells, key)):
            if e == 0:
                continue
            Q = k // l * P
            if not Q:
                continue
            Q._order = l
            phi = E.isogeny(Q,algorithm='factored')
            E, P = phi.codomain(), phi(P)
            key[i] -= 1
            k //= l
        round += 1
    return E
for ai in [a5,a4,a3,a2,a1,a0]:
    print('Timestamp K:',str(datetime.now()))
    D=dict()
    for i in tqdm(range(1,2**13)):
        priv=[2*bool(i&(1<<j)) for j in range(13)]+[0]*13
        Et=action(priv.copy(),9999,ai)
        x=to_montgomery(Et)
        D[x]=i
    for i in tqdm(range(1,2**13)):
        priv=[0]*13+[2*(bool(i&(1<<j))) for j in range(13)]
        Et=actioninv(priv.copy(),9999,a15)
        at=to_montgomery(Et)
        x=D.get(at,0)+D.get(p-at,0)
        if(x):
            print(i,x)
            break
print('Timestamp 3:',str(datetime.now()))

运行结果，耗时约 2h。

12

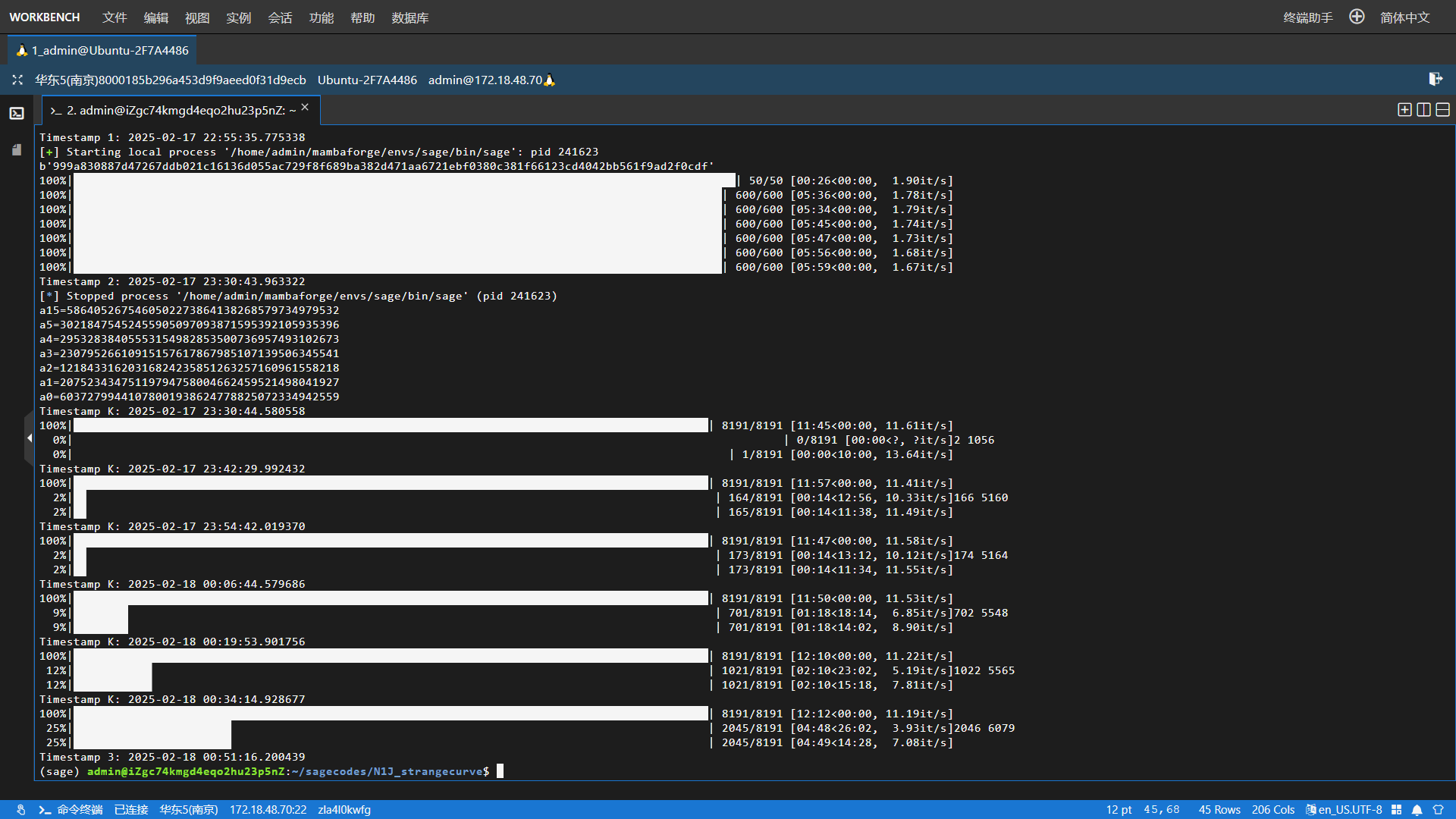
程序每一轮输出结果为：$(2,1056),(166,5160),(174,5164),(702,5548),(1022,5565),(2046,6079)$，那么整合这些结果和flag的密文，就可以解密了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
L=[(2,1056),(166,5160),(174,5164),(702,5548),(1022,5565),(2046,6079)]
A=[0]*26
for l,r in L:
    for i in range(13):
        A[13+i]+=bool(l&(1<<i))
        A[i]+=bool(r&(1<<i))

print(A)
from Crypto.Cipher import AES
from hashlib import *
from Crypto.Util.Padding import *

key = sha256(str(A).encode()).digest()
ciph=bytes.fromhex('999a830887d47267ddb021c16136d055ac729f8f689ba382d471aa6721ebf0380c381f66123cd4042bb561f9ad2f0cdf')
aes=AES.new(key,AES.MODE_ECB)
msg=aes.decrypt(ciph)
print(unpad(msg,16))
#flag{5a8f0629-d05c-441b-9b4c-17caf1b7b838}

但我们可以看到上面的进度条：这一部分那我们建立字典还是消耗了非常长的时间。

3.4.2 exp++

回顾刚才的思路不难注意到：$a_{15}$ 到 $a_{5}$ 的枚举中，我们所有私钥值 $e_i>5$ 的部分会被标记出来；而 $a_{15}$ 和 $a_{4}$ 的枚举中，所有私钥值 $e_i>4$ 的部分会被标记出来。后者标记的内容是完全包含前者的。因此可以进一步设置两个状态标记，消除掉不符合的情况，也就是 $a_4$ 的标记没有包含 $a_5$ 的情况，我们在这种情况下直接 contiue 掉，不做 action 以加速过程。

这一部分代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Hpos,Hneg=0,0
L=[]
for ai in [a5,a4,a3,a2,a1,a0]:
    print('Timestamp K:',str(datetime.now()))
    D=dict()
    for i in tqdm(range(1,2**13)):
        if((Hpos&i)!=Hpos):
            continue
        priv=[2*bool(i&(1<<j)) for j in range(13)]+[0]*13
        Et=action(priv.copy(),9999,ai)
        x=to_montgomery(Et)
        D[x]=i
    for i in tqdm(range(1,2**13)):
        if((Hneg&i)!=Hneg):
            continue
        priv=[0]*13+[2*(bool(i&(1<<j))) for j in range(13)]
        Et=actioninv(priv.copy(),9999,a15)
        at=to_montgomery(Et)
        x=D.get(at,0)+D.get(p-at,0)
        if(x):
            print(i,x)
            L.append((i,x))
            Hneg,Hpos=i,x
            break

那么完整的改善后的EXP就是：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
from pwn import *
from Crypto.Util.number import *
from tqdm import *
from sage.all import *
from datetime import *
STIME=datetime.now()
print('Timestamp 1:',str(datetime.now()))
sh=process(['sage','task16.sage'])
sh.recvuntil(b':')
ciph=sh.recvline(keepends=False).strip().decode()
print(ciph)

def get(x,tmz):        
    D=[]
    for i in tqdm(range(tmz)):
        sh.recvuntil(b'>')
        sh.sendline(str(x).encode())
        res=sh.recvline(keepends=False).decode()
        D.append(eval(res))
    def cmp(arg):
        return -arg[1]
    R=sorted([(i,D.count(i)) for i in set(D)],key=cmp)
    return R
D15=get(15,50)
D5=get(5,600)
D4=get(4,600)
D3=get(3,600)
D2=get(2,600)
D1=get(1,600)
D0=get(0,600)
print('Timestamp 2:',str(datetime.now()))

sh.close()
a15=D15[0][0]
a5,a4,a3,a2,a1,a0=[arr[1][0] for arr in [D5,D4,D3,D2,D1,D0]]
print(f'{a15=}')
print(f'{a5=}')
print(f'{a4=}')
print(f'{a3=}')
print(f'{a2=}')
print(f'{a1=}')
print(f'{a0=}')
ells = [*primes(3, 102)] + [149]
p = 4 * prod(ells) - 1
Fp=GF(p)
Fp2=GF(p**2)
def to_montgomery(E: EllipticCurve) -> int:
    Ep = E.change_ring(Fp).short_weierstrass_model()
    a, b = Fp(Ep.a4()), Fp(Ep.a6())
    P.<x> = PolynomialRing(Fp)
    r = (x^3 + a*x + b).roots()[0][0]
    s = sqrt(3 * r^2 + a)
    if not is_square(s):
        s = -s
    A = 3 * r / s
    return int(Fp(A))

def action(key: list, r: int,ma2:int) -> EllipticCurve:
    E = EllipticCurve(Fp2,[0,ma2,0,1,0])
    round = 0
    while any(key):
        E._order = (p + 1) ** 2
        k = prod([l for l, e in zip(ells, key) if e > 0])
        while True:
            P = E.lift_x(Fp.random_element())
            if randint(0, round == r) != (P.xy()[1] in Fp):
                break
        P *= (p + 1) // k
        for i, (l, e) in enumerate(zip(ells, key)):
            if e == 0:
                continue
            Q = k // l * P
            if not Q:
                continue
            Q._order = l
            phi = E.isogeny(Q,algorithm='factored')
            E, P = phi.codomain(), phi(P)
            key[i] -= 1
            k //= l
        round += 1
    return E
def actioninv(key: list, r: int,ma2:int) -> EllipticCurve:
    E = EllipticCurve(Fp2,[0,ma2,0,1,0])
    round = 0
    while any(key):
        E._order = (p + 1) ** 2
        k = prod([l for l, e in zip(ells, key) if e > 0])
        while True:
            P = E.lift_x(Fp.random_element())
            if randint(1,1) != (P.xy()[1] in Fp):
                break
        P *= (p + 1) // k
        for i, (l, e) in enumerate(zip(ells, key)):
            if e == 0:
                continue
            Q = k // l * P
            if not Q:
                continue
            Q._order = l
            phi = E.isogeny(Q,algorithm='factored')
            E, P = phi.codomain(), phi(P)
            key[i] -= 1
            k //= l
        round += 1
    return E
Hpos,Hneg=0,0
L=[]
for ai in [a5,a4,a3,a2,a1,a0]:
    print('Timestamp K:',str(datetime.now()))
    D=dict()
    for i in tqdm(range(1,2**13)):
        if((Hpos&i)!=Hpos):
            continue
        priv=[2*bool(i&(1<<j)) for j in range(13)]+[0]*13
        Et=action(priv.copy(),9999,ai)
        x=to_montgomery(Et)
        D[x]=i
    for i in tqdm(range(1,2**13)):
        if((Hneg&i)!=Hneg):
            continue
        priv=[0]*13+[2*(bool(i&(1<<j))) for j in range(13)]
        Et=actioninv(priv.copy(),9999,a15)
        at=to_montgomery(Et)
        x=D.get(at,0)+D.get(p-at,0)
        if(x):
            print(i,x)
            L.append((i,x))
            Hneg,Hpos=i,x
            break
print(ciph)
print('Timestamp 3:',str(datetime.now()))
A=[0]*26
for l,r in L:
    for i in range(13):
        A[13+i]+=bool(l&(1<<i))
        A[i]+=bool(r&(1<<i))
print(A)
from Crypto.Cipher import AES
from hashlib import *
from Crypto.Util.Padding import *
key = sha256(str(A).encode()).digest()
ciph=bytes.fromhex(ciph)
aes=AES.new(key,AES.MODE_ECB)
msg=aes.decrypt(ciph)
print(unpad(msg,16))
print(datetime.now()-STIME)

运行结果，还是缩短了一点时间的：

13

9.总结

不得不说有的题是真的难:(，需要的trick一时半会还真想不到，得去多积累。。。

2，3两个题官方只给了思路，没有给exp，在这里也算自己写了一下exp，或许记忆更深刻吧

后面准备再看看鸡块佬的那个 New Year Ring 4中的trick，那也是个RLWE的多项式构造，虽然他博客里面讲得很清楚了，但不自己写代码实现以下，或者测一下，可能还是不会太理解。

CTFSeason4
#ExpLog
25Feb1
http://example.com/2025/02/19/25Feb1/
作者
huangx607087
发布于
2025年2月19日
许可协议