Hgame25

Hgame 2025 Writeup

0. Introduction

之前那两周学同源相关内容 + 练车，导致Hgame没怎么看，然后开学后Hgame刚好结束，2月18日用一天半做了一下题，只能说跟21年22年相比，貌似确实难了很多。。。。

因为题目是18日做的，所以就不区分第一周第二周了，直接按题目分数排序了。

1.Ancient Recall(4pts,144sol)

先看看题目代码：

import random

Major_Arcana = ["The Fool", "The Magician", "The High Priestess","The Empress", "The Emperor", "The Hierophant","The Lovers", "The Chariot", "Strength","The Hermit", "Wheel of Fortune", "Justice","The Hanged Man", "Death", "Temperance","The Devil", "The Tower", "The Star","The Moon", "The Sun", "Judgement","The World"]
wands = ["Ace of Wands", "Two of Wands", "Three of Wands", "Four of Wands", "Five of Wands", "Six of Wands", "Seven of Wands", "Eight of Wands", "Nine of Wands", "Ten of Wands", "Page of Wands", "Knight of Wands", "Queen of Wands", "King of Wands"]
cups = ["Ace of Cups", "Two of Cups", "Three of Cups", "Four of Cups", "Five of Cups", "Six of Cups", "Seven of Cups", "Eight of Cups", "Nine of Cups", "Ten of Cups", "Page of Cups", "Knight of Cups", "Queen of Cups", "King of Cups"]
swords = ["Ace of Swords", "Two of Swords", "Three of Swords", "Four of Swords", "Five of Swords", "Six of Swords", "Seven of Swords", "Eight of Swords", "Nine of Swords", "Ten of Swords", "Page of Swords", "Knight of Swords", "Queen of Swords", "King of Swords"]
pentacles = ["Ace of Pentacles", "Two of Pentacles", "Three of Pentacles", "Four of Pentacles", "Five of Pentacles", "Six of Pentacles", "Seven of Pentacles", "Eight of Pentacles", "Nine of Pentacles", "Ten of Pentacles", "Page of Pentacles", "Knight of Pentacles", "Queen of Pentacles", "King of Pentacles"]
Minor_Arcana = wands + cups + swords + pentacles
tarot = Major_Arcana + Minor_Arcana
reversals = [0,-1]

Value = []
cards = []
YOUR_initial_FATE = []
while len(YOUR_initial_FATE)<5:
    card = random.choice(tarot)
    if card not in cards:
        cards.append(card)
        if card in Major_Arcana:
            k = random.choice(reversals)
            Value.append(tarot.index(card)^k)
            if k == -1:
                YOUR_initial_FATE.append("re-"+card)
            else:
                YOUR_initial_FATE.append(card)
        else:
            Value.append(tarot.index(card))
            YOUR_initial_FATE.append(card)
    else:
        continue
print("Oops!lets reverse 1T!")

FLAG=("hgame{"+"&".join(YOUR_initial_FATE)+"}").replace(" ","_")

YOUR_final_Value = Value
def Fortune_wheel(FATE):
    FATEd = [FATE[i]+FATE[(i+1)%5] for i in range(len(FATE))]
    return FATEd

for i in range(1):
    YOUR_final_Value = Fortune_wheel(YOUR_final_Value)
print(YOUR_final_Value)
YOUR_final_FATE = []
for i in YOUR_final_Value:
    YOUR_final_FATE.append(tarot[i%78])
print("Your destiny changed!\n",",".join(YOUR_final_FATE))
print("oh,now you GET th3 GOOd lU>k,^^")
"""
Oops!lets reverse 1T!
[2532951952066291774890498369114195917240794704918210520571067085311474675019, 2532951952066291774890327666074100357898023013105443178881294700381509795270, 2532951952066291774890554459287276604903130315859258544173068376967072335730, 2532951952066291774890865328241532885391510162611534514014409174284299139015, 2532951952066291774890830662608134156017946376309989934175833913921142609334]
Your destiny changed!
 Eight of Cups,Ace of Cups,Strength,The Chariot,Five of Swords
oh,now you GET th3 GOOd lU>k,^^
"""

其实这个题虽然写了一大堆，但其核心部分就是要根据最终拿到Value，求出原始的Value，最终可以直接得到flag。

注意到这样的递推式：

def Fortune_wheel(FATE):
    FATEd = [FATE[i]+FATE[(i+1)%5] for i in range(len(FATE))]
    return FATEd

该递推式执行了250次得到了最终的结果。可以发现这就是一个线性递推，尝试构建：

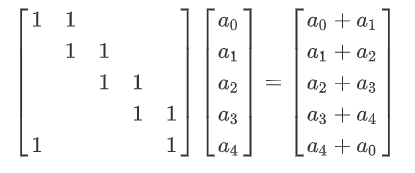
那么求原始值就是求左边矩阵的负250次幂乘上最终的Value向量，然后根据题目组flag的方式组成flag就OK了。

from sage.all import *
arr=[2532951952066291774890498369114195917240794704918210520571067085311474675019, 2532951952066291774890327666074100357898023013105443178881294700381509795270, 2532951952066291774890554459287276604903130315859258544173068376967072335730, 2532951952066291774890865328241532885391510162611534514014409174284299139015, 2532951952066291774890830662608134156017946376309989934175833913921142609334]

M=matrix([
    [1,1,0,0,0],
    [0,1,1,0,0],
    [0,0,1,1,0],
    [0,0,0,1,1],
    [1,0,0,0,1]
])

v=vector(arr)
ans=(M**-250)*v
print(ans)
# (-19, -20, 20, -15, 41)
Major_Arcana = ["The Fool", "The Magician", "The High Priestess","The Empress", "The Emperor", "The Hierophant","The Lovers", "The Chariot", "Strength","The Hermit", "Wheel of Fortune", "Justice","The Hanged Man", "Death", "Temperance","The Devil", "The Tower", "The Star","The Moon", "The Sun", "Judgement","The World"]
wands = ["Ace of Wands", "Two of Wands", "Three of Wands", "Four of Wands", "Five of Wands", "Six of Wands", "Seven of Wands", "Eight of Wands", "Nine of Wands", "Ten of Wands", "Page of Wands", "Knight of Wands", "Queen of Wands", "King of Wands"]
cups = ["Ace of Cups", "Two of Cups", "Three of Cups", "Four of Cups", "Five of Cups", "Six of Cups", "Seven of Cups", "Eight of Cups", "Nine of Cups", "Ten of Cups", "Page of Cups", "Knight of Cups", "Queen of Cups", "King of Cups"]
swords = ["Ace of Swords", "Two of Swords", "Three of Swords", "Four of Swords", "Five of Swords", "Six of Swords", "Seven of Swords", "Eight of Swords", "Nine of Swords", "Ten of Swords", "Page of Swords", "Knight of Swords", "Queen of Swords", "King of Swords"]
pentacles = ["Ace of Pentacles", "Two of Pentacles", "Three of Pentacles", "Four of Pentacles", "Five of Pentacles", "Six of Pentacles", "Seven of Pentacles", "Eight of Pentacles", "Nine of Pentacles", "Ten of Pentacles", "Page of Pentacles", "Knight of Pentacles", "Queen of Pentacles", "King of Pentacles"]
Minor_Arcana = wands + cups + swords + pentacles
tarot = Major_Arcana + Minor_Arcana

cards=[]
ans=list(ans)
for i in range(5):
    if(ans[i]<0):
        ans[i]=int(ans[i])^-1
        cards.append('re-'+tarot[ans[i]])
    else:
        cards.append(tarot[ans[i]])
FLAG=("hgame{"+"&".join(cards)+"}").replace(" ","_")
print(FLAG)
#hgame{re-The_Moon&re-The_Sun&Judgement&re-Temperance&Six_of_Cups}

2.SuprimeRSA(6pts,61sol)

好家伙，这竟然是个没见过的玩意，先看看题目代码。

from Crypto.Util.number import *
import random
from sympy import prime

FLAG=b'hgame{xxxxxxxxxxxxxxxxxx}'
e=0x10001

def primorial(num):
    result = 1
    for i in range(1, num + 1):
        result *= prime(i)
    return result
M=primorial(random.choice([39,71,126]))

def gen_key():
    while True:
        k = getPrime(random.randint(20,40))
        a = getPrime(random.randint(20,60))
        p = k * M + pow(e, a, M)
        if isPrime(p):
            return p

p,q=gen_key(),gen_key()
n=p*q
m=bytes_to_long(FLAG)
enc=pow(m,e,n)

print(f'{n=}')
print(f'{enc=}')

"""
n=787190064146025392337631797277972559696758830083248285626115725258876808514690830730702705056550628756290183000265129340257928314614351263713241
enc=365164788284364079752299551355267634718233656769290285760796137651769990253028664857272749598268110892426683253579840758552222893644373690398408
"""

题目的素数生成方式有点特殊，但你可以看出明显的小量 $k,a$，以及 $n=(k_1M+e^{a_1})(k_2M+e^{a_2})$，并且根据 $n$ 的规模，可以很快地确定三个选项中取的是 $39$ 。

当时先把 $e^{a_1}e^{a_2}$ 看作一个整体，然后把上面都式子展开 $n$ 写成 $M$ 进制的形式进行多项式处理。但发现 $e^{a_1}e^{a_2}$ 会超过 $M$，因此多项式的方式不管用。（虽然但是 n%M 的值还真能分解成两个素数的乘积）。。。

然后瞄了一眼week 1的WP，结果发现竟然是ROCA Attack。。。好家伙，上来就来论文题是吧？

那就点击 这个链接 下载github攻击代码，改改攻击参数，$n$ 就被分解了。。

from sage.all_cmdline import *

def coppersmith_howgrave_univariate(pol, modulus, beta, mm, tt, XX):
    """
    Taken from https://github.com/mimoo/RSA-and-LLL-attacks/blob/master/coppersmith.sage
    Coppersmith revisited by Howgrave-Graham

    finds a solution if:
    * b|modulus, b >= modulus^beta , 0 < beta <= 1
    * |x| < XX
    More tunable than sage's builtin coppersmith method, pol.small_roots()
    """
    #
    # init
    #
    dd = pol.degree()
    nn = dd * mm + tt

    #
    # checks
    #
    if not 0 < beta <= 1:
        raise ValueError("beta should belongs in [0, 1]")

    if not pol.is_monic():
        raise ArithmeticError("Polynomial must be monic.")

    #
    # calculate bounds and display them
    #
    """
    * we want to find g(x) such that ||g(xX)|| <= b^m / sqrt(n)

    * we know LLL will give us a short vector v such that:
    ||v|| <= 2^((n - 1)/4) * det(L)^(1/n)

    * we will use that vector as a coefficient vector for our g(x)

    * so we want to satisfy:
    2^((n - 1)/4) * det(L)^(1/n) < N^(beta*m) / sqrt(n)

    so we can obtain ||v|| < N^(beta*m) / sqrt(n) <= b^m / sqrt(n)
    (it's important to use N because we might not know b)
    """
    #
    # Coppersmith revisited algo for univariate
    #

    # change ring of pol and x
    polZ = pol.change_ring(ZZ)
    x = polZ.parent().gen()

    # compute polynomials
    gg = []
    for ii in range(mm):
        for jj in range(dd):
            gg.append((x * XX) ** jj * modulus ** (mm - ii) * polZ(x * XX) ** ii)
    for ii in range(tt):
        gg.append((x * XX) ** ii * polZ(x * XX) ** mm)

    # construct lattice B
    BB = Matrix(ZZ, nn)

    for ii in range(nn):
        for jj in range(ii + 1):
            BB[ii, jj] = gg[ii][jj]

    BB = BB.LLL()

    # transform shortest vector in polynomial
    new_pol = 0
    for ii in range(nn):
        new_pol += x ** ii * BB[0, ii] / XX ** ii

    # factor polynomial
    potential_roots = new_pol.roots()

    # test roots
    roots = []
    for root in potential_roots:
        if root[0].is_integer():
            result = polZ(ZZ(root[0]))
            if gcd(modulus, result) >= modulus ** beta:
                roots.append(ZZ(root[0]))
    return roots

from sage.all import *

def solve(M, n, a, m):
    # I need to import it in the function otherwise multiprocessing doesn't find it in its context
    base = int(65537)
    # the known part of p: 65537^a * M^-1 (mod N)
    known = int(pow(base, a, M) * inverse_mod(M, n))
    # Create the polynom f(x)
    F = PolynomialRing(Zmod(n), implementation='NTL', names=('x',))
    (x,) = F._first_ngens(1)
    pol = x + known
    beta = 0.1
    t = m+1
    # Upper bound for the small root x0
    XX = floor(2 * n**0.5 / M)
    # Find a small root (x0 = k) using Coppersmith's algorithm
    roots = coppersmith_howgrave_univariate(pol, n, beta, m, t, XX)
    # There will be no roots for an incorrect guess of a.
    for k in roots:
        # reconstruct p from the recovered k
        p = int(k*M + pow(base, a, M))
        if n%p == 0:
            return p, n//p

def roca(n):
    keySize = n.bit_length()
    if keySize <= 960:
        M_prime = 0x1b3e6c9433a7735fa5fc479ffe4027e13bea
        m = 5

    elif 992 <= keySize <= 1952:
        M_prime = 0x24683144f41188c2b1d6a217f81f12888e4e6513c43f3f60e72af8bd9728807483425d1e
        m = 4
        print("Have you several days/months to spend on this ?")

    elif 1984 <= keySize <= 3936:
        M_prime = 0x16928dc3e47b44daf289a60e80e1fc6bd7648d7ef60d1890f3e0a9455efe0abdb7a748131413cebd2e36a76a355c1b664be462e115ac330f9c13344f8f3d1034a02c23396e6
        m = 7
        print("You'll change computer before this scripts ends...")

    elif 3968 <= keySize <= 4096:
        print("Just no.")
        return None

    else:
        print("Invalid key size: {}".format(keySize))
        return None

    a3 = Zmod(M_prime)(n).log(65537)
    order = Zmod(M_prime)(65537).multiplicative_order()
    inf = a3 // 2
    sup = (a3 + order) // 2

    # Search 10 000 values at a time, using multiprocess
    # too big chunks is slower, too small chunks also
    chunk_size = 10000
    for inf_a in range(inf, sup, chunk_size):
        # create an array with the parameter for the solve function
        inputs = [((M_prime, n, a, m), {}) for a in range(inf_a, inf_a+chunk_size)]
        # the sage builtin multiprocessing stuff
        from sage.parallel.multiprocessing_sage import parallel_iter
        from multiprocessing import cpu_count

        for k, val in parallel_iter(cpu_count(), solve, inputs):
            if val:
                p = val[0]
                q = val[1]
                print("found factorization:\np={}\nq={}".format(p, q))
                return val

if __name__ == "__main__":
    n = 787190064146025392337631797277972559696758830083248285626115725258876808514690830730702705056550628756290183000265129340257928314614351263713241
    roca(n)

运行结果：

flag：hgame{ROCA_ROCK_and_ROll!}

看完第二个开始预感情况不妙了

3.Intergalactic Bound(7pts,45sol)

好家伙，这又是个啥题？THCurve又是啥？

from Crypto.Util.number import *
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from random import randint
import hashlib
from secrets import flag

def add_THCurve(P, Q):
    if P == (0, 0):
        return Q
    if Q == (0, 0):
        return P
    x1, y1 = P
    x2, y2 = Q
    x3 = (x1 - y1 ** 2 * x2 * y2) * pow(a * x1 * y1 * x2 ** 2 - y2, -1, p) % p
    y3 = (y1 * y2 ** 2 - a * x1 ** 2 * x2) * pow(a * x1 * y1 * x2 ** 2 - y2, -1, p) % p
    return x3, y3


def mul_THCurve(n, P):
    R = (0, 0)
    while n > 0:
        if n % 2 == 1:
            R = add_THCurve(R, P)
        P = add_THCurve(P, P)
        n = n // 2
    return R


p = getPrime(96)
a = randint(1, p)
G = (randint(1,p), randint(1,p))
d = (a*G[0]^3+G[1]^3+1)%p*inverse(G[0]*G[1],p)%p
x = randint(1, p)
Q = mul_THCurve(x, G)
print(f"p = {p}")
print(f"G = {G}")
print(f"Q = {Q}")

key = hashlib.sha256(str(x).encode()).digest()
cipher = AES.new(key, AES.MODE_ECB)
flag = pad(flag,16)
ciphertext = cipher.encrypt(flag)
print(f"ciphertext={ciphertext}")

"""
p = 55099055368053948610276786301
G = (19663446762962927633037926740, 35074412430915656071777015320)
Q = (26805137673536635825884330180, 26376833112609309475951186883)
ciphertext=b"k\xe8\xbe\x94\x9e\xfc\xe2\x9e\x97\xe5\xf3\x04'\x8f\xb2\x01T\x06\x88\x04\xeb3Jl\xdd Pk$\x00:\xf5"
"""

然后自己去查了一下，原来这种Curve的形式是：
$$
ax^3+y^3+1=dxy
$$
呃，奇怪的知识又增加了。

然后搜THCurve，搜到了羊城杯有过类似的题目，就是把这个曲线转成椭圆曲线的形式，然后做离散对数就OK了。

所以这个题最难的还是搞懂这是个啥曲线，然后怎么转成椭圆曲线。

代码就直接偷网上羊城杯那个题的wp了。

p = 55099055368053948610276786301
G = (19663446762962927633037926740, 35074412430915656071777015320)
Q = (26805137673536635825884330180, 26376833112609309475951186883)
ciphertext=b"k\xe8\xbe\x94\x9e\xfc\xe2\x9e\x97\xe5\xf3\x04'\x8f\xb2\x01T\x06\x88\x04\xeb3Jl\xdd Pk$\x00:\xf5"
Gx,Gy=G
Qx,Qy=Q
M=matrix(GF(p),[[-Gx**3,Gx*Gy],[-Qx**3,Qx*Qy]])
y=vector(GF(p),[Gy**3+1,Qy**3+1])
a,d=M.solve_right(y)
print(a,d)
from Crypto.Util.number import *
def calculate_coefficients(a, d):
    d_3 = d*inverse(3, p)%p             # d / 3
    tmp = a - d_3**3                    # a - d^3/27
    a0 = 1
    a1 = (-3 * d_3 * inverse(tmp, p))%p
    a3 = (-9 * inverse(tmp**2, p)) % p
    a2 = (-9 * d_3**2 * inverse(tmp**2, p))%p
    a4 = (-27 * d_3 * inverse(tmp**3, p))%p
    a6 = (-27 * inverse(tmp**4, p))%p
    
    return [a1, a2, a3, a4, a6]

aa = calculate_coefficients(a, d)
E = EllipticCurve(GF(p), aa)
def Herssian_to_Weierstrass(Point):
    x, y = Point
    u = ((-3 * inverse((a - d^3*inverse(27, p)), p)*x * inverse(d*x*inverse(3,p) - (-y) + 1, p))) % p
    v = ((-9 * inverse((a - d^3*inverse(27, p))^2, p) ) * (-y) * inverse(d*x*inverse(3,p) - (-y) + 1, p))%p
    return (u, v)


G = E(Herssian_to_Weierstrass(G))
Q = E(Herssian_to_Weierstrass(Q))
k = discrete_log(Q,G,operation='+')
print(k)
from Crypto.Cipher import AES
from hashlib import sha256
key=sha256(str(k).encode()).digest()
aes=AES.new(key,AES.MODE_ECB)
print(aes.decrypt(ciphertext))
"""
39081810733380615260725035189 8569490478014112404683314361
2633177798829352921583206736
b'hgame{N0th1ng_bu7_up_Up_UP!}\x04\x04\x04\x04'
"""

4.ezBag(7pts,75sol)

终于见到一个还算熟悉的题了，背包问题：

from Crypto.Util.number import *
import random
from Crypto.Cipher import AES
import hashlib
from Crypto.Util.Padding import pad
from secrets import flag

list = []
bag = []
p=random.getrandbits(64)
assert len(bin(p)[2:])==64
for i in range(4):
    t = p
    a=[getPrime(32) for _ in range(64)]
    b=0
    for i in a:
        temp=t%2
        b+=temp*i
        t=t>>1
    list.append(a)
    bag.append(b)
print(f'list={list}')
print(f'bag={bag}')

key = hashlib.sha256(str(p).encode()).digest()
cipher = AES.new(key, AES.MODE_ECB)
flag = pad(flag,16)
ciphertext = cipher.encrypt(flag)
print(f"ciphertext={ciphertext}")
list=[[2826962231, 3385780583, 3492076631, 3387360133, 2955228863, 2289302839, 2243420737, 4129435549, 4249730059, 3553886213, 3506411549, 3658342997, 3701237861, 4279828309, 2791229339, 4234587439, 3870221273, 2989000187, 2638446521, 3589355327, 3480013811, 3581260537, 2347978027, 3160283047, 2416622491, 2349924443, 3505689469, 2641360481, 3832581799, 2977968451, 4014818999, 3989322037, 4129732829, 2339590901, 2342044303, 3001936603, 2280479471, 3957883273, 3883572877, 3337404269, 2665725899, 3705443933, 2588458577, 4003429009, 2251498177, 2781146657, 2654566039, 2426941147, 2266273523, 3210546259, 4225393481, 2304357101, 2707182253, 2552285221, 2337482071, 3096745679, 2391352387, 2437693507, 3004289807, 3857153537, 3278380013, 3953239151, 3486836107, 4053147071], [2241199309, 3658417261, 3032816659, 3069112363, 4279647403, 3244237531, 2683855087, 2980525657, 3519354793, 3290544091, 2939387147, 3669562427, 2985644621, 2961261073, 2403815549, 3737348917, 2672190887, 2363609431, 3342906361, 3298900981, 3874372373, 4287595129, 2154181787, 3475235893, 2223142793, 2871366073, 3443274743, 3162062369, 2260958543, 3814269959, 2429223151, 3363270901, 2623150861, 2424081661, 2533866931, 4087230569, 2937330469, 3846105271, 3805499729, 4188683131, 2804029297, 2707569353, 4099160981, 3491097719, 3917272979, 2888646377, 3277908071, 2892072971, 2817846821, 2453222423, 3023690689, 3533440091, 3737441353, 3941979749, 2903000761, 3845768239, 2986446259, 3630291517, 3494430073, 2199813137, 2199875113, 3794307871, 2249222681, 2797072793], [4263404657, 3176466407, 3364259291, 4201329877, 3092993861, 2771210963, 3662055773, 3124386037, 2719229677, 3049601453, 2441740487, 3404893109, 3327463897, 3742132553, 2833749769, 2661740833, 3676735241, 2612560213, 3863890813, 3792138377, 3317100499, 2967600989, 2256580343, 2471417173, 2855972923, 2335151887, 3942865523, 2521523309, 3183574087, 2956241693, 2969535607, 2867142053, 2792698229, 3058509043, 3359416111, 3375802039, 2859136043, 3453019013, 3817650721, 2357302273, 3522135839, 2997389687, 3344465713, 2223415097, 2327459153, 3383532121, 3960285331, 3287780827, 4227379109, 3679756219, 2501304959, 4184540251, 3918238627, 3253307467, 3543627671, 3975361669, 3910013423, 3283337633, 2796578957, 2724872291, 2876476727, 4095420767, 3011805113, 2620098961], [2844773681, 3852689429, 4187117513, 3608448149, 2782221329, 4100198897, 3705084667, 2753126641, 3477472717, 3202664393, 3422548799, 3078632299, 3685474021, 3707208223, 2626532549, 3444664807, 4207188437, 3422586733, 2573008943, 2992551343, 3465105079, 4260210347, 3108329821, 3488033819, 4092543859, 4184505881, 3742701763, 3957436129, 4275123371, 3307261673, 2871806527, 3307283633, 2813167853, 2319911773, 3454612333, 4199830417, 3309047869, 2506520867, 3260706133, 2969837513, 4056392609, 3819612583, 3520501211, 2949984967, 4234928149, 2690359687, 3052841873, 4196264491, 3493099081, 3774594497, 4283835373, 2753384371, 2215041107, 4054564757, 4074850229, 2936529709, 2399732833, 3078232933, 2922467927, 3832061581, 3871240591, 3526620683, 2304071411, 3679560821]]
bag=[123342809734, 118191282440, 119799979406, 128273451872]
ciphertext=b'\x1d6\xcc}\x07\xfa7G\xbd\x01\xf0P4^Q"\x85\x9f\xac\x98\x8f#\xb2\x12\xf4+\x05`\x80\x1a\xfa !\x9b\xa5\xc7g\xa8b\x89\x93\x1e\xedz\xd2M;\xa2'

题目给了 $4$ 组数据，构成了一个 $64$ 位的背包问题，要求出密钥解得flag。

背包问题的格构造方法在 2021 年的 LatticeNotes5 中已经提到过了，回顾一下：

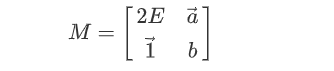
上面的矩阵中：$E$ 为单位矩阵，$\vec a$ 为每个物品重量的列向量，$\vec 1$ 为全 $1$ 向量，$b$ 为物品重量之和。对 $M$ 进行LLL，可以得到一个最后一个分量为 $0$，其他分量只有 $-1$ 和 $1$ 的向量，分别对应着 $1$ 和 $0$。

这边插播一句：其实也可以将 $2E$ 换成 $E$，$\vec 1$ 换成 $\vec 0$，$b$ 换为 $-b$，这样解出来的就恰好是向量 $0,1$。但事实上，这种构造方法并不常用，因为这样构造会将行列式的值缩小为原来的一半，降低解出目标向量的概率（这个思想后面一个题也会用到）。

然而，题目给了 $4$ 组数据，那么构造的矩阵就是

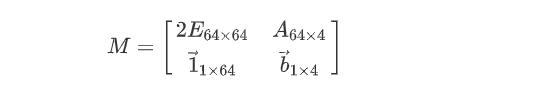
然而，即使是这样，仍然解不出正确向量。考虑到最后 4 列在目标向量中的分量为 $0$。因此可以给最后 4 列乘上 $2^{2000}$，强行增加最后四列权重，解得最短向量即为目标向量。

from Crypto.Util.number import *
a=#题目中给出的list
bag=[123342809734, 118191282440, 119799979406, 128273451872]
ciphertext=b'\x1d6\xcc}\x07\xfa7G\xbd\x01\xf0P4^Q"\x85\x9f\xac\x98\x8f#\xb2\x12\xf4+\x05`\x80\x1a\xfa !\x9b\xa5\xc7g\xa8b\x89\x93\x1e\xedz\xd2M;\xa2'
M=block_matrix(ZZ,[
    [2*identity_matrix(64),matrix(a).T],
    [matrix([1]*64),matrix(bag)]
])
B=diagonal_matrix([1]*64+[2**2000]*4)
M3L=(M*B).LLL()*(B**-1)
for vec in M3L:
    if(max(vec)==1 and min(vec)==-1):
        print(vec)
        break
#(-1, -1, -1, 1, 1, -1, -1, -1, -1, -1, 1, -1, 1, 1, -1, 1, -1, 1, 1, -1, 1, 1, -1, -1, 1, -1, -1, 1, -1, 1, -1, -1, -1, 1, -1, 1, -1, -1, -1, 1, -1, -1, -1, -1, -1, -1, 1, 1, 1, 1, 1, 1, -1, -1, 1, 1, 1, -1, -1, 1, -1, -1, -1, -1, 0, 0, 0, 0)

mask=2**64-1
s=0
for i in range(64):
    s+=((vec[i]==-1)<<i)
print(s)
from Crypto.Cipher import AES
from hashlib import *
key = sha256(str(s).encode()).digest()
aes = AES.new(key, AES.MODE_ECB)
print(aes.decrypt(ciphertext))
#17739748707559623655
#b'hgame{A_S1mple_Modul@r_Subset_Sum_Problem}\x06\x06\x06\x06\x06\x06'

这个mask虽然没用到，但其实有的时候也是会用到的：因为目标向量有时会多个 $-1$ 的系数，导致解出的比特全是反的，第一遍得不到结果。如果出现这种情形，直接异或一下mask，就给比特全翻转回来了！

5.sieve (7pts,140sol)

一看就是个oi✌出的题，可以看出，我们要求出 $65537^2/6$ 内的素数个数和所有数字的素数个数和欧拉函数之和。

#sage
from Crypto.Util.number import bytes_to_long
from sympy import nextprime

FLAG = b'hgame{xxxxxxxxxxxxxxxxxxxxxx}'
m = bytes_to_long(FLAG)

def trick(k):
    if k > 1:
        mul = prod(range(1,k)) 
        if k - mul % k - 1 == 0:
            return euler_phi(k) + trick(k-1) + 1
        else:
            return euler_phi(k) + trick(k-1)
    else:
        return 1

e = 65537
p = q = nextprime(trick(e^2//6)<<128)
n = p * q
enc = pow(m,e,n)
print(f'{enc=}')
#enc=2449294097474714136530140099784592732766444481665278038069484466665506153967851063209402336025065476172617376546

因此正解是素数筛和杜教筛，但后者我不会写，考虑到这个值为 $715849728$，并不是很大，可以用 $O(n\log n)$ 的复杂度逐个求解。

不过据说sage中可以直接枚举 euler_phi 并求和，在服务器上单核跑的时间为 40 分钟左右，反正也能出。

#include <bits/stdc++.h>
using namespace std;

const unsigned N = 715849728;
const unsigned M = 26760;
bool isPrime[N + 1];
unsigned *eulerPhi = new unsigned [N + 1];
unsigned long long S = 0ULL;
unsigned long long T = 0ULL;
unsigned *primes = new unsigned[40000000];  
int primeCount = 0;

int main() {
    memset(isPrime, 1, sizeof(isPrime));
    isPrime[0] = isPrime[1] = 0;
    for (int i = 2; i <= M; i++) {
        if (isPrime[i]) {
            for (int j = 2 * i; j <= N; j += i) {
                isPrime[j] = 0;
            }
        }
    }
    for (int i = 2; i <= N; i++) {
        if (isPrime[i]) {
            primes[primeCount++] = i;
        }
    }
    S = primeCount;  // 直接存储质数数量
    cout<<S<<endl;
    for (int i = 0; i <= N; i++) {
        eulerPhi[i] = i;
    }

    for (int i = 0; i < S; i++) {
        unsigned p = primes[i];
        for (unsigned j = p; j <= N; j += p) {
            if(eulerPhi[j]%p!=0) cout<<"ERROR"<<endl;
            unsigned long long tmp=eulerPhi[j]/p;
            if(tmp*(p-1)>0xFFFFFFFFULL) cout<<"ERROR"<<endl;
            eulerPhi[j] = 1ULL*tmp*(p-1);  // 避免重复乘除，提高精度
        }
    }

    for (int i = 0; i <= N; i++) {
        T += eulerPhi[i];
    }

    cout << T << endl;

    delete[] eulerPhi;
    delete[] primes;
    return 0;
}
/*
37030583
155763335410704472
40s,3.5GB
*/

求出需要的两个值之后，直接解就OK了

from gmpy2 import *
from Crypto.Util.number import *
e = 65537
p = q = next_prime((155763335410704472+37030583)<<128)
n=p*q
phi=(p*(p-1))
d=inverse(e,phi)
c=2449294097474714136530140099784592732766444481665278038069484466665506153967851063209402336025065476172617376546
print(long_to_bytes(pow(c,d,n)))
#hgame{sieve_is_n0t_that_HArd}

6.SPiCa(8pts,21sol)

看到题目中 $0.035$，$A$ 为随机 $0,1$ 矩阵，大概率能够猜到是正交格。

from Crypto.Util.number import getPrime, long_to_bytes,bytes_to_long
from secrets import flag
from sage.all import *

def derive_M(n):
    iota=0.035
    Mbits=int(2 * iota * n^2 + n * log(n,2))
    M = random_prime(2^Mbits, proof = False, lbound = 2^(Mbits - 1))
    return Integer(M)

m = bytes_to_long(flag).bit_length()
n = 70
p = derive_M(n)


F = GF(p)
x = random_matrix(F, 1, n)
A = random_matrix(ZZ, n, m, x=0, y=2)
A[randint(0, n-1)] = vector(ZZ, list(bin(bytes_to_long(flag))[2:]))
h = x*A

with open("data.txt", "w") as file:
    file.write(str(m) + "\n")
    file.write(str(p) + "\n")
    for item in h:
        file.write(str(item) + "\n")

ref：HSSP与正交格学习笔记 - 0xFFFF

正交格主要是用于解决 $A\vec x\equiv \vec b \pmod p$ 的问题，其中 $A$ 为 $0,1$ 的未知置矩阵，$\vec x$ 为秘密向量，我们只知道最终向量 $\vec b$ 和模数 $p$，其余内容我们均不知道。

题目中，我们得到向量 $\vec h=\vec xA$ ，$A$ 符合上述的特点。由于 $\vec x$ 为行向量，$A$ 可以看作 $\vec a_0,\vec a_1,…,\vec a_{m-1}$ 这 $m$ 个行向量组成的矩阵。

我们先回顾一下线性代数的知识（真巧，18号写这个，19号就要学矩阵论）

对于一个 $m$ 行 $n$ 列的矩阵（如果 $m\not=n$），那么这个矩阵的秩一定不超过 $\min(m,n)$。根据链接中的内容，我们可以得到行空间、列空间、左0空间、右0空间的概念：

行空间：$\vec xA=\vec b$ 中，所有 $\vec b$ 构成的空间，此时 $A$ 的每一行构成空间的基底向量。

列空间：$A\vec x=\vec b$ 中，所有 $\vec b$ 构成的空间，此时 $A$ 的每一列构成空间的基底向量。

左0空间：满足 $\vec xA=\vec 0$ 的所有 $\vec x$ 构成的集合，在sagemath中为 A.left_kernel().matrix()。其个数为 $m-r+1$，$r$ 为 $A$ 中互相线性无关的行向量个数。

右0空间：满足 $A\vec x=\vec 0$ 的所有 $\vec x$ 构成的集合，在sagemath中为 A.right_kernel().matrix()。其个数为 $n-r+1$，$r$ 为 $A$ 中互相线性无关的列向量个数。

性质：行空间和右0空间正交，列空间与左0空间正交。

由于题目中 $\vec xA=\vec h$，因此，我们可以先设法构造 $\vec u$，使得 $\vec u\cdot\vec h=0$，也就是 $\sum_{i=0}^{m-1}u_ih_i\equiv 0\pmod p$。

写成矩阵的形式就是（为方便展示，以三个分量为例）：

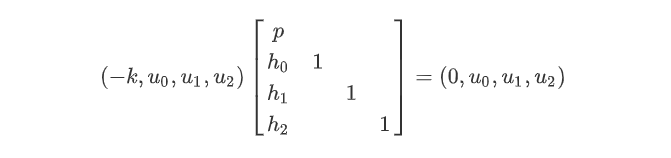
很明显，为了求出 $\vec u$ ，我们需要对上面的矩阵LLL处理，设上面的矩阵为 $M$，那么就可以得到 $M_{3L}$。

n,m=70,247
p=24727704801291912268835129736340977567569865784366882566681759917843647658060231409536848349518003784121914409876944135933654762801696486121844572452922377222301017649192408619831637530961997845860817966791811403512683444831050730277
h=#题目中给出的数据
M=block_matrix([
    [p,zero_matrix(1,m)],
    [matrix(h).T,identity_matrix(m)]
])
M3L=M.LLL()

这样，我们就得到了向量 $\vec u$，满足 $\vec u\cdot \vec h\equiv 0\pmod p$

u=vector(GF(p),M3L[0])
Mp=matrix(GF(p),M)
u*Mp==u
#True

然后，我们可以用 $M_{3L}$ 的前 $m-n$ 列，构造格 $L_x$，然后求 $L_x$ 的右 0 空间（因为题目中是 $\vec xA$ 得到的是行空间，因此要求右 0 空间），构造 $L_c$，然后对 $L_c$ 做BKZ就能够得到原始矩阵 $A$（对于 $0/1$ 决策，使用BKZ算法比LLL算法有更高概率得到正确结果），这一部分可以参考给出的链接的内容，这一部分代码如下：

Lxo = matrix(ZZ, M3L[:m-n])
Lxc = Lxo.right_kernel(algorithm='pari').matrix() # faster
Lxc3L=Lxc.BKZ()
for vline inn Lxc3L:
    print(vline)

我们期待找出一个仅包含 $0,1$ 的向量，但发现得到的向量基本都会包含 $-1,0,1$ 三个数字。这和之前做背包密码时产生的问题相同。因此，可以借鉴其方法，构造矩阵 $\left[\dfrac{\vec 1}{2L_c}\right]$，这样原矩阵 $A$ 就变成了 $2A-1$ ，使得所有向量的分量均为 $±1$，某种意义上来说，也算一种系数平衡方法吧。

那么最后的exp如下（当然，如果解不出来，可以对 $V_{3L}$ 取反再尝试一下）：

n,m=70,247
p=24727704801291912268835129736340977567569865784366882566681759917843647658060231409536848349518003784121914409876944135933654762801696486121844572452922377222301017649192408619831637530961997845860817966791811403512683444831050730277
h=#题目中给出的数值
M=block_matrix([
    [p,zero_matrix(1,m)],
    [matrix(h).T,identity_matrix(m)]
])
M3L=M.LLL()
Lxo = matrix(ZZ, M3L[:m-n])
Lxc = Lxo.right_kernel(algorithm='pari').matrix() # faster
V=block_matrix(ZZ,[[matrix([1]*(m+1))],[2*Lxc]])
V3L=V.BKZ()
from Crypto.Util.number import *
for i in range(1,V3L.nrows()):
    vec=V3L[i]
    s=0
    for j in range(1+m):
        s*=2
        s+=(vec[j]==1)
    s=long_to_bytes(s)
    if(b'hgame{' in s):
        print(s)

9.总结

今年Hgame比21年和22年的难太多了，0xGame2024也是，感觉难度和20，21年不是一个档次的（当时21年我还怕出难了，Predict1和Predict2借鉴了21年Hgame的夺宝大冒险，其实就是直接抄的，但最终看来题目还是比0xGame2020难）。

Hgame2022的题我附件还在（因为那个时候我CTF已经处于一个半退役的状态了），并且我手中还保存了当年SACC寒假打卡的材料，看了看学弟Schen交给我的打卡记录，感觉题目和21年的相仿，并且22年的题目我那个寒假也做了一些，貌似四周的题目也都是一天AK的（但当时好像就没打理博客了，所以找不到22年的做题记录，后面有空补一篇）。。。

不过话说回来，这几年CTF咋出了这么多东西，我CTF两年的空窗期究竟发生了什么？