NCTF25Wp

NCTF 2025 WP by 0x5593e78d

0.Introduction

周末简单看了看NCTF的三个密码题，感觉这三个题其实不是很难

AES 的注入攻击根本看不懂，为啥Crypto开始写ShellCode了？？后面有空再学吧。。。

1.Sign

看一眼题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from Crypto.Util.number import *
from os import getenv
from Crypto.Util.Padding import pad
from random import Random
from Crypto.Cipher import AES
from hashlib import md5

string = open('secret.txt').read().strip().encode()
flag = getenv('FLAG').encode()

if __name__=='__main__':
    Keys = []
    for m in string:
        f = FHE()
        s = long_to_bytes(Random().getrandbits(20000))
        for i in s[4:]:
            Keys.extend(f.encrypt([i]))

        for i in s[:4]:
            Keys.extend(f.encrypt([i * (m & 0x03) % 0x101]))
            m >>= 2
        
    assert len(Keys) == 30000

    print(f'[+] Your ciphertext: {AES.new(md5(string).digest(),AES.MODE_ECB).encrypt(pad(flag,16)).hex()}')
    input(f'[+] The keys to retrieve the global internet connection are as follows:')
    for i in range(30000):
        print(f'[+] {Keys[i]}')

util.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from os import urandom
from Crypto.Util.number import *

def getrandint(n:int):
    return int.from_bytes(urandom(n//8+1),'big') % pow(2,n)

class FHE:
    def __init__(self):
        self.p = getPrime(77)
        self.pubkeys = []
        for _ in range(16):
            self.pubkeys.append(self.p * getrandint(177) + (getrandint(17) << 8))
    def encrypt(self,msg):
        result = []
        for m in msg:
            tmp = 0
            shuffle_base = urandom(16)
            for i in shuffle_base:
                x,y = divmod(i,16)
                tmp += x*self.pubkeys[y] + y*self.pubkeys[x]
            result.append(tmp + m)
        return result

看到FHE，貌似是一个全同态加密。对于单个字符 $m$：题目先生成了 $20000$ 个随机比特，也就是 $2500$ 随机字节。然后用同一个FHE对象进行加密。加密方式也很简单：随机生成 $16$ 个生成 $Ap+256B$，然后进行未知的变换，最后直接加上 $m$ 就OK了。

注意到下面的内容：

1
2
3
4
shuffle_base = urandom(16)
for i in shuffle_base:
    x,y = divmod(i,16)
    tmp += x*self.pubkeys[y] + y*self.pubkeys[x]

虽然我们不知道如何变换的，但 $X(Ap+256B)+Y(Cp+256D)$ 经过未知变换后，仍然具有 $Ap+256B$ 的形式。由于 $p$ 是 $77$ 比特，$A$ 是 $177$ 比特，$B$ 是 $17$ 比特。那么 $256B$ 就是 $25$ 比特。可以发现这个误差并不是很大，考虑 AGCD。

因此对于一组 $2500$ 个数据来说，可以取前 $120$ 个数据，构造（以四个为例，实际上最后取了 $120$ 个，4 个应该不够，这里是为了举例）：

1

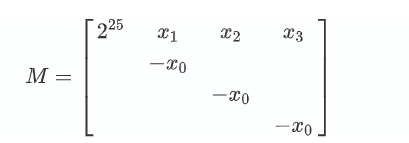
这样就有
$$
(A_0,A_1,A_2,A_3)\mathbf M= (A_02^{25},A_0B_1-A_1B_0,A_0B_2-A_2B_0,A_0B_3-A_3B_0)
$$
那么 $A_0$ 的值就有了，直接整除就可以得到 模数 $q$，然后就能够得到 $2500$ 个明文字节了。

得到加密内容后，我们发现 getrandbits(20000) 转成字节后，用于处理的是前 4 个字节，那么我们得到的真实字节是 $2496$ 个。这样恰好构成 $19968$ 比特。因此可以直接调工具（工具我自己写的，细看21年7月10日博文）解决。

解决后往后预测一组数据，简单算一下，就能够拿到一个 $m$ 字节了。题目给了 $30000$ 个数据，说明加密的字节数为 $12$。

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
from pwn import *
from tqdm import *
sh=remote('39.106.16.204',64018)
sh.recvuntil(b':')
c=sh.recvline(keepends=False).strip().decode()
print(c)
sh.recvuntil(b'[+]')
sh.sendline(b'\n')
D=[]
for i in tqdm(range(30000)):
    sh.recvuntil(b'[+]')
    line=sh.recvline()
    D.append(int(line))
from mttool import *
ANS=[]
for T in range(12):
    DT=D[T*2500:T*2500+2500]
    M=block_matrix(ZZ,
        [
            [2**25,matrix(DT[0+1:0+120])],
            [0,-identity_matrix(119)*DT[0+0]]
        ]
    )
    M3L=M.LLL()
    p=DT[0]//(abs(M3L[0][0])//2**25)
    r20k=[]
    for i in range(2500):
        r20k.append(DT[i]%p%256)
    states=[]
    for i in range(624):
        y=(r20k[4*i]<<24)
        y|=(r20k[4*i+1]<<16)
        y|=(r20k[4*i+2]<<8)
        y|=(r20k[4*i+3])
        states.append(y)
    F=MT19937()
    F.setstate(states[::-1])
    last4=long_to_bytes(F.getstate())
    rr=[]
    rt=r20k[-4:]
    for i in range(4):
        for j in range(4):
            if(j*last4[i]%257==rt[i]):
                rr.append(j)
                break
    print(len(rr))
    mi=sum([rr[i]*4**i for i in range(4)])
    ANS.append((mi))
c=bytes.fromhex(c)
from Crypto.Cipher import AES
from hashlib import md5
print(AES.new(md5(bytes(ANS)).digest(),AES.MODE_ECB).decrypt(c))
#b'nctf{f3426f2c-846b-4f83-8249-06e6e6e37617}\x06\x06\x06\x06\x06\x06'

2.Arcahv

套娃题X1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
from Crypto.Util.number import *
from os import urandom,getenv
from functools import reduce
from Crypto.Cipher import AES

class LCG:
    def __init__(self,seed:int) -> None:
        self.p = getPrime(1024)
        self.a = getPrime(1023)
        self.b = getPrime(1023)
        self.status = seed

    def next(self) -> int:
        ret = self.status
        self.status = (self.status * self.a + self.b) % self.p
        return ret
    
def crystal_trick(m:bytes) -> bytes:
    m = bytearray(m)
    for i in range(len(m)):
        m[i] = reduce(lambda x,y: x^y^urandom(1)[0],m[:i],m[i])
    return m

class RSA:
    def __init__(self):
        p = getStrongPrime(1024)
        q = getStrongPrime(1024)
        self.p = p
        self.N = p * q
        self.e = 65537
        self.d = pow(self.e, -1, (p-1)*(q-1))

    def encrypt(self,m:int) -> int:
        return pow(m,self.e,self.N)
    
    def decrypt(self,c:int) -> int:
        return pow(c,self.d,self.N) 

class MyRSA1(RSA):
    def encrypt(self,m:bytes) -> bytes:
        return super().encrypt(int.from_bytes(m)).to_bytes(256)
    
    def decrypt(self,c:bytes) -> bytes:
        return super().decrypt(int.from_bytes(c)).to_bytes(256)

class MyRSA2(RSA):
    def encrypt(self,m:bytes) -> bytes:
        return pow(int.from_bytes(m),self.e,self.N).to_bytes(256,'little')
    
    def decrypt(self,c:bytes) -> bytes:
        m = pow(int.from_bytes(c),self.d,self.N).to_bytes(256,'little')
        print('Hibiscus is here to trick your decryption result!!')
        return crystal_trick(m)

menu = '''
Welcome to NCTF 2025 arcahv challenge!

--- Menu ---
[1] View encrypted flag and hint
[2] Play with the decryption orcale
[3] Get some random numbers for fun
[4] Exit

Your Option > '''


if __name__=='__main__':
    print('Loading, please wait...')
    
    # flag = open('flag.txt').read().strip().encode()
    flag = getenv('FLAG').encode()
    attempts = 75
    r1 = MyRSA1()
    r2 = MyRSA2()
    hint1 = r2.encrypt(r1.p.to_bytes(128))

    key = urandom(16)
    hint2 = AES.new(key,AES.MODE_ECB).encrypt(r1.N.to_bytes(256))

    def flag_and_hint():
        print(f'Encrypted flag: {r1.encrypt(flag).hex()}')
        print(f'Hint1: {hint1.hex()}')
        print(f'Hint2: {hint2.hex()}')

    def rsachal(): 
        global attempts

        print("Since you didn't v Hibiscus 50 on crazy thursday, Hibiscus decided to do some trick on your decryption result!")
        print(f'Your pubkey:({hex(r2.N)[2:]},{hex(r2.e)[2:]})')

        while attempts > 0:
            if input('Do you still want to try decryption(y/[n])?') != 'y':
                break

            c = bytes.fromhex(input(f'You have {attempts} remaining access to decryption orcale!\nYour ciphertext(in hex):'))
            print(f'Result: {r2.decrypt(c).hex()}')
            attempts -= 1
        
        if attempts == 0:
            print('Unfortunately, you are out of decryption attempts! Come back again on nctf2026 ~')

    
    def lcgchal():
        lcg = LCG(int.from_bytes(key))

        print('Tempering with LCG generator, please wait...')
        while urandom(1)[0] & 0xff:
            lcg.next()
        
        hexnums = ''.join(hex(lcg.next())[2:] for _ in range(5))
        if len(hexnums) % 16:
            hexnums = hexnums.zfill((len(hexnums) // 16 + 1) * 16)
        
        idx = 0
        while input('Do you want another unsigned long long number(y/[n])?') == 'y':
            print(int(''.join(hexnums[idx:idx+16]),16))
            idx = (idx + 16) % len(hexnums)

    def bye():
        print('Hope you have fun during the challenge XD:)')
        exit(0)

    fundc = {1:flag_and_hint,2:rsachal,3:lcgchal,4:bye}

    while True:
        opt = input(menu)
        if len(opt) == 0 or opt not in '1234':
            opt = '4'
        fundc[int(opt)]()

题目给了两个RSA系统：第一个RSA系统正常，第二个RSA系统加密时返回的内容是反着的。并且测试一下可以发现：解密时只会正确地返回第一个字符（相当于明文的低位）。

我们已知的内容是：R2的公钥、flag用R1加密的密文、R1的素数 $p$ 用 R2 加密的结果，以及 R1 的模数 $n$ 用 AES 加密的结果。。

那么肯定是先解处 R1 的模数 $n_1$：根据LCG的生成方式，如果每个LCG的最高那位十六进制位不为 $0$ （指的是写成 $256$ 位十六进制下），那么我们就可以运行 $80$ 次得到 LCG 的连续五个 state $a_0,a_1,a_2,a_3,a_4$。那么简单推下式子：设 $T_i=a_{i+1}-a_{i}$，那么有
$$
T_{1+i}\equiv aT_{i-1} \pmod p
$$
那么连续三个 $T_i$ 就可以得到 $p$：
$$
T_1^2-T_0T_2\equiv A^2T_0^2-T_0AT_1\equiv A^2T_0^2-A^2T_0^2\equiv 0\pmod p
$$
我们可以得到两组这样的式子，那么求一下最大公约数就可以得到 $p$ 了。如果验证结果不是素数，那么简单试除一下也可以。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def calcpab(arr):
    assert len(arr)==5
    trr=[arr[i+1]-arr[i] for i in range(4)]
    drr=[trr[i+1]**2-trr[i]*trr[i+2]for i in range(2)]
    p=GCD(drr[0],drr[1])
    print(p)
    if(p==1):
        exit(0)
    while(not isPrime(p)):
        for i in range(2,1000):
            while(p%i==0):
                p//=i
                if(p==1):
                    exit(0)
                print(p)
    assert isPrime(p)
    a=trr[1]*inverse(trr[0],p)%p
    b=(arr[1]-a*arr[0])%p
    return p,a,b

求出 $p,A,B$ 后，由于加密密钥不超过 $2^{256}$，而模数是 $2^{1024}$ 级别的素数，那么直接逆回去，找到一个不超过 $2^{256}$ 的值就OK了。我们就得到了 $n_1$。

然后求 $p_1$ 的过程就很繁琐了：首先我们要将得到的内容转化成 bytes，倒过来再 bytes_to_long，才能够得到实际的密文值。由于我们每次进行解密，只知道明文的第一字节，也就是实际明文的低位。这很明显是一个 ParityOracle问题，我们给 $c$ 乘上 ${256}e$，那么解密回来就是 $256m$。由于存在取模，因此最低一字节并非 $\mathtt{00H}$，而是要看到 $256m$ 整除 $n_2$ 的值。如果这个值是 $0$，那么会返回 $\mathtt{00H}$，如果这个值是 $k$，那么会返回 $-n_2k\mod 256$ 的值。 假如 $n_2\equiv 83\pmod {256}$，当服务器返回最最低字节为 $\mathtt{ADH}$ 时，也就是 $173\equiv -83\pmod {256}$，说明明文的值位于 $\left[\dfrac{n}{256},\dfrac{2n}{256}\right]$ 中。

当然，如果举个模 $5$ 的例子可能更方便些（猜猜这个表格在我博客中的哪里能找到）

2

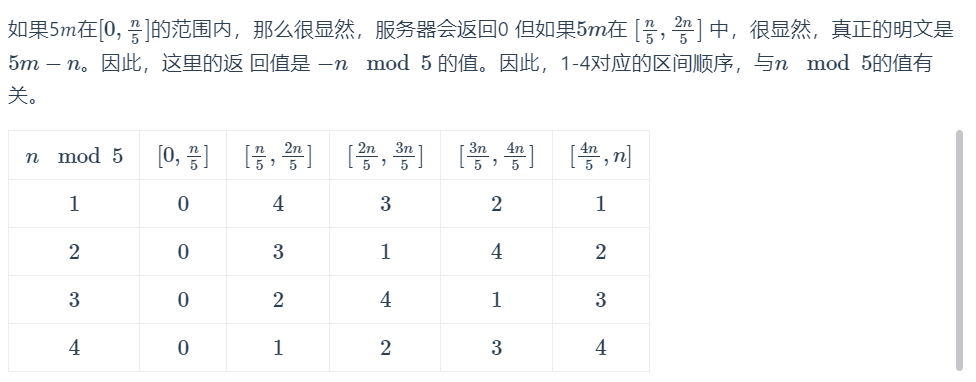
然而，测了第一次，发现 $75$ 次机会除了第一次外，全都返回了 $00$。因为模数 $n_2$ 是 $2048$ 位，而 $p_1$ 是 $1024$ 位。那么直接从 $256^{125e}c$ 开始测！这里先给出到此为止的exp。该exp结束后，不再需要交互，后面转手工。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
from Crypto.Util.number import *
from Crypto.Cipher import AES
from pwn import *
context.log_level='debug'
def calcpab(arr):
    assert len(arr)==5
    trr=[arr[i+1]-arr[i] for i in range(4)]
    drr=[trr[i+1]**2-trr[i]*trr[i+2]for i in range(2)]
    p=GCD(drr[0],drr[1])
    print(p)
    if(p==1):
        exit(0)
    while(not isPrime(p)):
        for i in range(2,1000):
            while(p%i==0):
                p//=i
                if(p==1):
                    exit(0)
                print(p)
    assert isPrime(p)
    a=trr[1]*inverse(trr[0],p)%p
    b=(arr[1]-a*arr[0])%p
    return p,a,b

sh=remote('39.106.16.204',17402)
sh.recvuntil(b'>')
sh.sendline(b'3')
recvD=[]
for i in range(81):
    sh.recvuntil(b'?')
    sh.sendline(b'y')
    x=int(sh.recvline())
    recvD.append(x)
if(recvD[-1]-recvD[0]):
    print('Not this time')
    exit(0)
arrD=[]
for i in range(5):
    s=0
    for j in range(16):
        s<<=64
        s|=recvD[i*16+j]
    arrD.append(s)
print(arrD)
p,a,b=calcpab(arrD[:])
key=arrD[0]

while(key>2**256):
    key-=b
    key*=inverse(a,p)
    key%=p

print(p,a,b)
print(key)
sh.sendline(b'n')
sh.recvuntil(b'>')
sh.sendline(b'1')
sh.recvuntil(b':')
encflag=sh.recvline(keepends=False).strip().decode()
sh.recvuntil(b':')
hint1=sh.recvline(keepends=False).strip().decode()
sh.recvuntil(b':')
hint2=sh.recvline(keepends=False).strip().decode()
print(encflag)
print(hint1)
print(hint2)
key=long_to_bytes(key)
encN1=bytes.fromhex(hint2)
aes=AES.new(key,AES.MODE_ECB)
n1=aes.decrypt(encN1)
n1=bytes_to_long(n1)
print(n1)
sh.recvuntil(b'>')
sh.sendline(b'2')
sh.recvuntil(b':')
recv=sh.recvline(keepends=False)
print(recv)
recv=recv[1:-2].split(b',')
n2=int(recv[0],16)
print(hex(n2))
e=65537

X=[]
print(hint1)
cpbyte=bytes.fromhex(hint1)
v=bytes_to_long(cpbyte[::-1])

for i in range(1):
    sh.recvuntil(b'?')
    sh.sendline(b'y')
    sh.recvuntil(b'x):')
    sendmsg=hex(v)[2:]
    sh.sendline(hex(v)[2:].zfill(512).encode())
    sh.recvuntil(b'Result:')
    res=sh.recvline(keepends=False).strip()
    ch=(res[:2].decode())
    X.append(ch)
v=v*pow(256,125*e,n2)%n2
for i in range(74):
    sh.recvuntil(b'?')
    sh.sendline(b'y')
    sh.recvuntil(b'x):')
    sendmsg=hex(v)[2:]
    sh.sendline(hex(v)[2:].zfill(512).encode())
    sh.recvuntil(b'Result:')
    res=sh.recvline(keepends=False).strip()
    ch=(res[:2].decode())
    X.append(ch)
    print(X)
    v=v*pow(256,e,n2)%n2
print(n1)
print(n2)
print(encflag)
sh.interactive()

上面的运行结果：

3

然后直接开始爆破范围（注意！第一个2f 不能用）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
arr=['2f', '00', '00', '00', '29', '17', 'ac', '63', '2a', '12', 'b4', 'd7', '7f', '8e', '7d', '79', '30', 'f0', '8d', 'f6', '80', 'bf', '12', '01', '8d', '62', '3a', 'fd', '84', '0d', '32', 'c8', '3b', 'a7', 'f0', '24', 'f0', '15', 'a2', '5f', '4a', 'de', 'dd', '1c', '98', '5f', '8f', '7a', 'f4', 'c8', 'a3', '9b', 'd0', '9b', '55', 'd4', 'ba', 'e0', '08', '6a', 'a8', '0a', '9f', 'cc', '5f', '19', '41', '68', '7a', '0e', '0b', 'f1', '8e', 'eb', 'd4']

for i in range(len(arr)):
    arr[i]=int(arr[i],16)
arr=[arr[0]]+[0]*124+arr[1:] #补0
n1=27200726861606479413732540105769910106442930230059237006054788241492464198104226383006410896382163376887470890204817762296150365816982716578179794854120618733079054476439310808699368362524368009863477241538507564128979615816719656677628033340699504650141751106657147711531182871752313833548093903353942659291504321147175513860126538171856141771130055268089395190693480487394926612586609197282096272323143729032822596264092788535977083098902273595611970396931862238894253416076466663232326332414509580222889346000134628190970397400801864490308861607242999251439680729962967555209719581660252320905410364920401446239303
n2=24866822730629741379543089342079365341084319942174960331446452232117371422271533566140696929308567448991245082987740709784575137043273683337512757363573795517125236929453001640592938073197621050370978049041795713829175921955882351394322171396408329945985047022211319396826484094373519811807038760516472914568410858958127418474325676604209564451818287720761393703919618496538122341926550323739647239342218647444489004430681441241694935875888014926811056992516155152050668980222129873115657480401875436724468589908377383686709144009265881121060716778695399105731759893237880088418588599471238660076946418515349084241879
enc='89b83be7fb18744eb4de33cbfd303154a8f73e48025da5e3dd6ac34158c007e5d0110bb7cf5d676e87bd52f28b07d5144d952bd067c2ed00f675eba80a081c2dfe07145f85de497c5bf5563e149f72ba41b436c8391714c12185f20bd87a254f2574a90068d59422c4717e16c3a932f46b38f75c11ef15d60fa7b6ac4148b769165af92098576c99d78ad01be7be3b1d3542e14173018efc16786e5c015a213c4f9fe556e8729746162f14082d3b6782ffb49dcab301d2eab04f9634e2ac26dbe86ecc9f95e0e16ff24bcc8b3f4041739ee19a5d5ecfca6bce6db7323324e009d5cfad1fab53763b305c73997074ac60d65c1563be557266bd797777189f9141'
D=[((-n2%256*i)%256,i)for i in range(256)]
D=dict(D)
RR2=0
for i in range(len(arr)):
	RR2*=256
	RR2+=D[arr[i]]
L,R=0,n2
for ind in arr[1:]:
    d=(R-L)//256
    A=[(L+i*d,L+i*d+d) for i in range(256)]
    L,R=A[D[ind]]
print(L)
print((R-L).nbits())
#172799521024601879001741885595218933847281902792617444774942977554593120275188061514104260564097524853443062177738541830447967000437522706147190799882378433642226305269611270977983760855382680208247566854983914040974739748794608596554135230293528885495707702590808348319342820440892742201222307253441666908364
#464

上面的运行完了，调试可以发现 $R-L$ 还有 $464$ 比特差距。好在这个差距小于 $512$ 了，因此相当于 $p_1$ 高位已知。直接flatter求解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
from subprocess import check_output
from re import findall
from sage.all import *

def flatter(M):  # flatter
    z = "[[" + "]\n[".join(" ".join(map(str, row)) for row in M) + "]]"
    ret = check_output(["flatter"], input=z.encode())
    return matrix(M.nrows(), M.ncols(), map(int, findall(b"-?\\d+", ret)))

def matrix_overview(BB):  # see the shape of matrix
    for ii in range(BB.dimensions()[0]):
        a = ('%02d ' % ii)
        for jj in range(BB.dimensions()[1]):
            a += '0' if BB[ii, jj] == 0 else 'X'
            if BB.dimensions()[0] < 60:
                a += ' '
        print(a)

def Small_Roots_Univariate(f, X=None, beta=1.0, epsilon=None):  # 多项式f,X,beta,epsilon

    delta = f.degree()  # 度delta
    N = f.parent().characteristic()  # 模数N
    PR = PolynomialRing(ZZ, 'x')
    x = PR.gen()

    Zm = f.base_ring()  # Zmod(N)
    f = f.change_ring(ZZ)  # ZZ下f(x)
    if not f.is_monic():  # 首一
        f = f.monic()  # f = f * f[delta].inverse_mod(N)

    m = ceil(max(beta * beta / (delta * epsilon), 7 * beta / delta))  # m
    t = floor(delta * m * (1 / beta - 1))  # t
    print('m={}, t={}'.format(m, t))

    f_ij = []
    for i in range(m):
        for j in range(delta):
            f_ij.append(x ** j * N ** (m - i) * f ** i)  # shift g_ij(x)
    for i in range(t):
        f_ij.append(x ** i * f ** m)  # shift h_i(x)

    monomials = []
    for g in f_ij:
        monomials += g.monomials()  # 统计所有出现的单项 x^i
    monomials = sorted(set(monomials))  # 去重并排序

    M = Matrix(ZZ, len(f_ij), len(monomials))  # 行数为多项式个数，列数为所有单项可能个数
    for i in range(M.nrows()):
        for j, monomial in enumerate(monomials):
            M[i, j] = f_ij[i].monomial_coefficient(monomial) * monomial.subs(x=X)  # g_ij(xX)和h_i(xX)
    matrix_overview(M)  # see
    assert M.nrows() == M.ncols()  # 方阵 nrows()=ncols()
    B = flatter(M)  # flater加速
    print('end LLL')
    for j in range(M.nrows()):  # 得到f(xX)，构建f(x)，求根检验
        Cx = sum(ZZ(B[j, i] // monomials[i](X)) * monomials[i] for i in range(M.ncols()))  # construct polynomial,
        R = Cx.roots()  # get roots
        roots = [Zm(r[0]) for r in R if abs(r[0]) <= X]  # check x0<=X
        roots = [r for r in roots if gcd(N, ZZ(f(r))) >= ZZ(floor(N ** beta))]  # check gcd(f(x_0),N)>N^beta
        if roots:
            return roots  # 返回root


from datetime import *
from Crypto.Util.number import *
ubit=465
for i in range(1):
    N=27200726861606479413732540105769910106442930230059237006054788241492464198104226383006410896382163376887470890204817762296150365816982716578179794854120618733079054476439310808699368362524368009863477241538507564128979615816719656677628033340699504650141751106657147711531182871752313833548093903353942659291504321147175513860126538171856141771130055268089395190693480487394926612586609197282096272323143729032822596264092788535977083098902273595611970396931862238894253416076466663232326332414509580222889346000134628190970397400801864490308861607242999251439680729962967555209719581660252320905410364920401446239303
    h=1813821521390952791907851592772095409997054947935376553145948003754050882342394467279913359361865116548590145033659198493606802741628130182020602936736423567685054012340
    print(hex(N))
    print(hex(h<<ubit))
    PR = PolynomialRing(Zmod(N), 'x')
    x = PR.gen()
    f = (h << ubit) + x
    tstart=datetime.now()
    roots = Small_Roots_Univariate(f, 2 ** ubit, 0.49, 0.007)
    tend=datetime.now()
    p=Integer(h<<ubit)|Integer(roots[0])
    print(hex(p),Integer(N)%Integer(p)==0,str(tend-tstart))
#0xf6131ea06fb167d8ab673b8589cfb41baa057bfe7881114ebf866dfb444d12e798689934991e86abf7a91cbaf35c9ca1ec2aaec6c42d1258c7062e5428fe3000aee860f53769a0558f4a9b15a3646dce7f4463efc86272ba55c4aca999519418d5f5a285b63ba12af7c09a61ce3230be3a548df531c08eddded3a1aa8001212f True 0:01:27.556792

最后十六进制果然是以 $\mathtt{2FH}$ 结尾，说明求解正确。然后直接解密就OK。

1
2
3
4
5
6
7
p=0xf6131ea06fb167d8ab673b8589cfb41baa057bfe7881114ebf866dfb444d12e798689934991e86abf7a91cbaf35c9ca1ec2aaec6c42d1258c7062e5428fe3000aee860f53769a0558f4a9b15a3646dce7f4463efc86272ba55c4aca999519418d5f5a285b63ba12af7c09a61ce3230be3a548df531c08eddded3a1aa8001212f 
q=n1//p
e=65537
from Crypto.Util.number import *
d=inverse(e,(p-1)*(q-1))
long_to_bytes(pow(int(enc,16),d,n1))
#b'nctf{ffb15e99-51d4-47e0-821c-1432f1ceb0c6}'

3.Qiyun

有人在这个题浪费了两坤时，我不说是谁。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
from Crypto.Util.number import *
from os import getenv,urandom
from hashlib import sha256
from random import randint

class ECDSA:
    def __init__(self):
        self.p = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF
        self.a = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC
        self.b = 0x28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93
        self.n = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
        self.Gx = 0x32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7
        self.Gy = 0xBC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0
        self.G = (self.Gx,self.Gy)

        self.d = getPrime(232)
        self.Q = self.mul(self.d,self.G)
        assert self.is_on_curve(self.Q)

    def is_on_curve(self, point):
        if point is None:
            return True
        x, y = point
        return (y**2 - x**3 - self.a * x - self.b) % self.p == 0

    def add(self, p1, p2):
        if p1 is None or p2 is None:
            return p1 if p2 is None else p2

        x1, y1 = p1
        x2, y2 = p2

        if x1 == x2 and y1 != y2:
            return None
        if x1 == x2:
            m = (3 * x1 * x1 + self.a) * pow(2 * y1, -1,  self.p) % self.p
        else:
            m = (y2 - y1) * pow((x2 - x1) % self.p, -1, self.p) % self.p
        
        x3 = (m * m - x1 - x2) % self.p
        y3 = (m * (x1 - x3) - y1) % self.p
        return (x3, y3)

    def mul(self, k:int, P:tuple[int,int]):
        if P is None:
            return None
        
        R = None        
        while k > 0:
            if k & 1:
                R = self.add(R, P)
            P = self.add(P,P)
            k >>= 1
        return R

    def generate_key_pair(self):
        return self.d,self.Q

    def sign(self, message):
        while True:
            k = randint(1, self.n - 1)
            P = self.mul(k, self.G)
            if P is None:
                continue
            
            r = P[0] % self.n
            if r == 0:
                continue

            s = (pow(k,-1,self.n) * (int.from_bytes(sha256(message).digest())+ self.d * r)) % self.n
            if s != 0:
                return (r, s)

    def verify(self, m:bytes, r:int,s:int):
        if not (1 <= r < self.n and 1 <= s < self.n):
            return False
        
        u1 = (int.from_bytes(sha256(m).digest()) * pow(s,-1,self.n)) % self.n
        u2 = (r * pow(s,-1,self.n)) % self.n

        if u1 == 0 or u2 == 0:
            return False

        P = self.add(self.mul(u1, self.G), self.mul(u2, self.Q))        
        return P[0] % self.n == r

class RSA:
    def __init__(self,d:int):
        p = getStrongPrime(1024)
        q = getStrongPrime(1024)
        
        assert GCD(d,(p-1)*(q-1)) == 1

        self.N = p * q
        self.d = d
        self.e = pow(d,-1,(p-1)*(q-1))

    def encrypt(self,m:int,idx:int):
        return pow(m,self.e ^ (1 << idx),self.N)
    
def check():
    r,s = list(map(int,input('Give me your signature:').split()))
    if e.verify(f'nctf2024-{urandom(1).hex()}'.encode(),r,s):
        print(f'Congratulations! Here is your flag: {getenv("FLAG")}')
        exit()
    else:
        print('Wrong!')


if __name__=='__main__':
    e = ECDSA()
    print('Can you navigate yourself through QiYun Valley with only the encryption orcale?')

    menu = '''
--- Menu ---
[1] Initialize encryption orcale
[2] Check your signature
[3] Exit'''

    while True:
        print(menu)
        opt = input('Your option:').strip()
        
        if opt=='1':
            print('Generating new public key pair for you...')
            rsa = RSA(e.d ** 4)

            while input("Enter 'e' for encryption or other to exit:").strip() == "e":
                m = int(input('Enter your message:'),16)
                x = int(input('Where do you want to interfere?'))

                print(f'Result:{hex(rsa.encrypt(m,x))[2:]}')

        elif opt=='2':
            check()
        
        elif opt=='3':
            print('Bye~')
            exit()

        else:
            print('Invalid option')

题目给出了一个ECDSA和一个RSA，其中 ECDSA 的私钥为 $232$ 位长度的 $d$，RSA的私钥为 $d^4$，长度为 $928$ 位。题目只有两个选择：一是生成一个 RSA 系统并只有加密服务，二是验签。

既然要求 $d$，那就要考察 RSA 这边。但 RSA 这边 $e,n$ 都不给。不过RSA可以选择在加密时选择一个比特进行翻转，并给出这个比特翻转后的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
class RSA:
    def __init__(self,d:int):
        p = getStrongPrime(1024)
        q = getStrongPrime(1024)
        
        assert GCD(d,(p-1)*(q-1)) == 1

        self.N = p * q
        self.d = d
        self.e = pow(d,-1,(p-1)*(q-1))

    def encrypt(self,m:int,idx:int):
        return pow(m,self.e ^ (1 << idx),self.N)

既然要求 $n$，那很显然，$e$ 肯定时奇数，并且题目没有说只能发送正数过去，那就发一个 $-1$ 过去，在第 $9999$ 位翻转，那得到的值就是 $-1$ 的奇数次方模 $n$ 的值，也就是 $n-1$。 那么 $n$ 我们就有了。。。

然后，我们可以发送 $2,0$ 过去。由于 $e$ 是奇数，因此 $e\oplus1=e-1$，我们就得到了 $2^{e-1}$ 次方，乘个 $2$ 取余数就得到了 $2^e$ 次方。

那么后面就是一比特一比特的爆破了。 我们可以计算 $2^{e\oplus2^k}$ 和 $2^e$ 对比。如果 $2^{e\oplus2^k}\times 2^k\equiv 2^e\pmod n$，那么说明 $e\oplus 2^k=e-2^k$，这一比特为 $1$。如果是 $2^{e\oplus2^k}\times 2^{-k}\equiv 2^e\pmod n$，那么这一比特就是 $0$ 了。这样我们就逐比特爆破得到了 $e$，交互时长大概五分钟。

如果我们退出，然后重新进去，服务器就会生成一组不同的数据，但私钥还是 $d^4$。这就说明这是个很明显的共私钥指数攻击。算一下界：
$$
\frac{1}{2}-\frac{1}{2(r+2)}>\frac{928}{2048}\rightarrow r>8.67
$$
因此取 $9$ 组数据就OK了，当然这里为了保险，取了 $10$ 组。构造矩阵LLL就能够拿到 $d^4$ 了，然后开根就是 $d$。

这样交互就是 $50$ 分钟 ，本地测一次也要 $20$ 分钟，调了我一下午。。。

有了 $d$ 之后，ECDSA 就可以验签了。然而这边也是随机的。也需要交互好几次（是为了防止我这种懒人最后一步手动操作吗）。。。

exp（注意ECDSA虽然是复制的题目中的，但有两处有微小改动，已经标明）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
from pwn import *
from Crypto.Util.number import *
from sage.all import *
from tqdm import *
# sh=process(['python3','task.py'])
sh=remote('39.106.16.204',18476)
def untilsend(endflag,msg):
    sh.recvuntil(endflag)
    sh.sendline(msg)
T=10
Ns=[]
Es=[]
for _ in range(T):
    print(f'Round {_+1}/{T} Start!')
    untilsend(b':',b'1')
    untilsend(b':',b'e')
    untilsend(b':',b'-1')
    untilsend(b'?',b'9999')
    sh.recvuntil(b':')
    ni=int(sh.recvline(keepends=False),16)+1
    Ns.append(ni)
    encTwo=None
    ebits=[-2]*2048
    ebits[0]=1
    for i in tqdm(range(2048)):
        untilsend(b':',b'e')
        untilsend(b':',b'2')
        untilsend(b'?',str(i).encode())
        sh.recvuntil(b':')
        res=int(sh.recvline(keepends=False),16)#*2%ni
        
        if(i==0):
            encTwo=res*2%ni
        else:
            if(res*pow(2,1<<i,ni)%ni==encTwo):
                ebits[i]=1
            elif(res*pow(2,-(1<<i),ni)%ni==encTwo):
                ebits[i]=0
            else:
                print('something wrong')
                exit(0)
    ei=0
    for i in range(2048):
        ei+=ebits[i]<<(i)
    Es.append(ei)
    untilsend(b':',b'q')
print(Ns)
print(Es)
#for debug
with open('datarecv41.txt','w') as fpp:
    fpp.write(str(Ns))
    fpp.write('\n')
    fpp.write(str(Es))
Nm=Integer(max(Ns)).nth_root(2,truncate_mode=1)[0]
M=[[0 for __ in range(1+T)] for _ in range(1+T)]
M[0][0]=Nm
for i in range(T):
    M[0][i+1]=Es[i]
    M[i+1][i+1]=-Ns[i]
M=matrix(ZZ,M)
M3L=M.LLL()
dM=abs(M3L[0][0])
d4=dM//Nm
d,judg=(Integer(d4).nth_root(4,truncate_mode=1))
if(not judg):
    print('error!')
    exit(0)
else:
    print('d =',d)

from hashlib import sha256
class ECDSA:
    def __init__(self):
        self.p = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF
        self.a = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC
        self.b = 0x28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93
        self.n = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
        self.Gx = 0x32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7
        self.Gy = 0xBC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0
        self.G = (self.Gx,self.Gy)

        self.d = d #d我们求出来了，直接用
        self.Q = self.mul(self.d,self.G)
        assert self.is_on_curve(self.Q)

    def is_on_curve(self, point):
        if point is None:
            return True
        x, y = point
        return (y**2 - x**3 - self.a * x - self.b) % self.p == 0

    def add(self, p1, p2):
        if p1 is None or p2 is None:
            return p1 if p2 is None else p2

        x1, y1 = p1
        x2, y2 = p2

        if x1 == x2 and y1 != y2:
            return None
        if x1 == x2:
            m = (3 * x1 * x1 + self.a) * pow(2 * y1, -1,  self.p) % self.p
        else:
            m = (y2 - y1) * pow((x2 - x1) % self.p, -1, self.p) % self.p
        
        x3 = (m * m - x1 - x2) % self.p
        y3 = (m * (x1 - x3) - y1) % self.p
        return (x3, y3)

    def mul(self, k:int, P:tuple[int,int]):
        if P is None:
            return None
        
        R = None        
        while k > 0:
            if k & 1:
                R = self.add(R, P)
            P = self.add(P,P)
            k >>= 1
        return R

    def generate_key_pair(self):
        return self.d,self.Q

    def sign(self, message):
        while True:
            k = 1 #随机数取 1 就OK了
            P = self.mul(k, self.G)
            if P is None:
                continue
            
            r = P[0] % self.n
            if r == 0:
                continue

            s = (pow(k,-1,self.n) * (int.from_bytes(sha256(message).digest())+ self.d * r)) % self.n
            if s != 0:
                return (r, s)

    def verify(self, m:bytes, r:int,s:int):
        if not (1 <= r < self.n and 1 <= s < self.n):
            return False
        
        u1 = (int.from_bytes(sha256(m).digest()) * pow(s,-1,self.n)) % self.n
        u2 = (r * pow(s,-1,self.n)) % self.n

        if u1 == 0 or u2 == 0:
            return False

        P = self.add(self.mul(u1, self.G), self.mul(u2, self.Q))        
        return P[0] % self.n == r
ecdsa=ECDSA()
r,s=ecdsa.sign(b'nctf2024-99')
while(1):
    untilsend(b':',b'2')
    untilsend(b':',(f'{r} {s}').encode())
    result=sh.recvline()
    if(b'flag' in result):
        print(result)
        break
sh.interactive()

运行结果：

4

CTFSeason4
#WriteUp
NCTF25Wp
http://example.com/2025/03/25/NCTF25Wp/
作者
huangx607087
发布于
2025年3月25日
许可协议