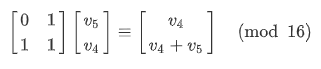ciscn2026wp1

CISCN2026 Crypto Writeup

0.Introduction

23岁的倒数第二天，最后一次打CISCN，自己二期CTF也就结束了。

23岁的最后一天，还是选择二次退役了（未完成的赛事会打完，但不再主动报名新的比赛）。CTF断断续续打了 3 年半，覆盖1，2，3，4，9，10，11七个学期，总体看来也算是比较长的了。从2020年8月24日第一次学CTF Crypto，到2022年第一次打CISCN后，8月24日退役后大三为保研卷了一年GPA。再到2024年9月研究生入学后，利用以前的基础继续打了1年半（其实正儿八经打的只有半年），这一次，因为自己科研任务加重，加上毕业压力，还是决定退役了。近期改论文感觉整个人已经快崩掉了。

不得不说今年CISCN题目质量简直不敢恭维，和去年完全没法比，不仅仅是Crypto了，你就看到Pwn+RE+Crypto，三个方向一共13题，单一个Web就11题，就WEBCTF了呗。

1

CTF一期：$2020.08.24\sim2022.08.24$

CTF二期：$2024.09.19\sim2025.12.29$

1.ECDSA

第一个题，发现解得特别快（按理说预期应该是做LLL的），如果禁AI的话，不应该这么快

先看一下题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#!/usr/bin/env python3
from ecdsa import SigningKey, NIST521p
from hashlib import sha512
from Crypto.Util.number import long_to_bytes
import random
import binascii
import sys

digest_int = int.from_bytes(sha512(b"Welcome to this challenge!").digest(), "big")
curve_order = NIST521p.order
priv_int = digest_int % curve_order
priv_bytes = long_to_bytes(priv_int, 66)
sk = SigningKey.from_string(priv_bytes, curve=NIST521p)
vk = sk.verifying_key

f_pub = open("public.pem", "wb")
f_pub.write(vk.to_pem())
f_pub.close()

def nonce(i):
    seed = sha512(b"bias" + bytes([i])).digest()
    k = int.from_bytes(seed, "big")
    return k

msgs = [b"message-" + bytes([i]) for i in range(60)]
sigs = []

for i, msg in enumerate(msgs):
    k = nonce(i)
    sig = sk.sign(msg, k=k)
    sigs.append((binascii.hexlify(msg).decode(), binascii.hexlify(sig).decode()))

f_sig = open("signatures.txt", "w")
for m, s in sigs:
    f_sig.write("%s:%s\n" % (m, s))
f_sig.close()

本来还想搞懂一下这个ECDSA的pem格式，尝试运行了一下函数看看内容。

结果运行了两次，输出的priv_int竟然一样。。。

1
2
priv_int
mpz(11786190273906782566706300546504742629011900435269701041731697414027484824601255112180676531145294320443777235338538357924760601782873554458995940394745073)

所以直接输出priv_int，然后做md5

1
2
md5(str(priv_int).encode()).hexdigest()
#581bdf717b780c3cd8282e5a4d50f3a0

最终flag：

1
flag{581bdf717b780c3cd8282e5a4d50f3a0}

2.ezFlag

拿到一个程序，应该是LINUX下的，拖进IDA点进去Main函数，可以得到：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
int __cdecl main(int argc, const char **argv, const char **envp)
{
  __int64 v3; // rax
  __int64 v4; // rax
  char v6[32]; // [rsp+0h] [rbp-50h] BYREF
  __int64 v7; // [rsp+20h] [rbp-30h] BYREF
  int v8; // [rsp+2Ch] [rbp-24h] BYREF
  char v9; // [rsp+33h] [rbp-1Dh]
  int i; // [rsp+34h] [rbp-1Ch]
  unsigned __int64 v11; // [rsp+38h] [rbp-18h]

  std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::basic_string(v6, argv, envp);
  std::operator<<<std::char_traits<char>>(&_bss_start, "Enter password: ");
  std::getline<char,std::char_traits<char>,std::allocator<char>>();
  if ( (unsigned __int8)std::operator!=<char>((__int64)v6, (__int64)"V3ryStr0ngp@ssw0rd") )
  {
    v3 = std::operator<<<std::char_traits<char>>(&_bss_start, "Wrong password!");
    std::ostream::operator<<(v3, &std::endl<char,std::char_traits<char>>);
  }
  else
  {
    std::operator<<<std::char_traits<char>>(&_bss_start, "flag{");
    std::ostream::flush((std::ostream *)&_bss_start);
    v11 = 1LL;
    for ( i = 0; i <= 31; ++i )
    {
      v9 = f(v11);
      std::operator<<<std::char_traits<char>>(&_bss_start, (unsigned int)v9);
      std::ostream::flush((std::ostream *)&_bss_start);
      if ( i == 7 || i == 12 || i == 17 || i == 22 )
      {
        std::operator<<<std::char_traits<char>>(&_bss_start, "-");
        std::ostream::flush((std::ostream *)&_bss_start);
      }
      v11 *= 8LL;
      v11 += i + 64;
      v8 = 1;
      std::chrono::duration<long,std::ratio<1l,1l>>::duration<int,void>(&v7, &v8);
      std::this_thread::sleep_for<long,std::ratio<1l,1l>>((__int64)&v7);
    }
    v4 = std::operator<<<std::char_traits<char>>(&_bss_start, "}");
    std::ostream::operator<<(v4, &std::endl<char,std::char_traits<char>>);
  }
  std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::~basic_string(v6);
  return 0;
}

很显然中间是一个 for 循环，每次取一位 $v_9=f(v_{11})$，然后 $v_{11}=(8v_{11}+64)\mod 2^{64}$。但出了七八位flag之后，运行开始非常慢，以至于无法在合理时间内得到flag。

然后点进去 $f$ 函数看看：思路非常明朗，就是做一个简单的运算：$v_4,v_5\rightarrow v_4+v_5,v_4$，在模 $16$ 的意义下进行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
__int64 __fastcall f(unsigned __int64 a1)
{
  __int64 v2; // [rsp+10h] [rbp-20h]
  unsigned __int64 i; // [rsp+18h] [rbp-18h]
  __int64 v4; // [rsp+20h] [rbp-10h]
  __int64 v5; // [rsp+28h] [rbp-8h]

  v5 = 0LL;
  v4 = 1LL;
  for ( i = 0LL; i < a1; ++i )
  {
    v2 = v4;
    v4 = ((_BYTE)v5 + (_BYTE)v4) & 0xF;
    v5 = v2;
  }
  return *(unsigned __int8 *)std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::operator[](
                               &K,
                               v5);
}

很显然，有斐波那契函数的特征，那就上斐波那契函数的矩阵递推：

2

当然简单测试一下

1
2
3
4
5
6
7
8
#Sagemath
def f(a11):
    v5,v4=0,1
    M=[[0,1],[1,1]]
    M=matrix(Zmod(16),M)
    v=vector([v5,v4])
    v=(M**(a11))*v
    return v[0]

由于每次迭代都是 $v_{11}$ 步，而 $v_{11}$ 有个递推式，那就先求出每次 $v_{11}$ 的迭代次数，并进行记录。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include<bits/stdc++.h>
using namespace std;
long long f(unsigned long long a1)
{
  long long v2; // [rsp+10h] [rbp-20h]
  unsigned long long i; // [rsp+18h] [rbp-18h]
  long long v4; // [rsp+20h] [rbp-10h]
  long long v5; // [rsp+28h] [rbp-8h]

  v5 = 0LL;
  v4 = 1LL; 
  for ( i = 0LL; i < a1; ++i )
  {
    v2 = v4;
    v4 = ((char)v5 + (char)v4) & 0xF;
    v5 = v2;
  }
  return v5;
}

int main() 
{
	unsigned long long v11=1;
	for(int i=0;i<=31;i++)
	{
//		printf("%llu\n",v11);
		char v9=f(v11%24);
		printf("%d %llu\n",v9,v11);
		v11 *= 8LL;
    	v11 += i + 64;
	}
}
/*
Output:
1 1
0 72
13 641
7 5194
2 41619
13 333020
9 2664229
8 21313902
1 170511287
11 1364090368
2 10912723017
1 87301784210
5 698414273755
0 5587314190116
5 44698513521005
15 357588108168118
2 2860704865345023
5 22885638922760264
1 183085111382082193
8 1464680891056657626
9 11717447128453261091
13 1505856659078330732
5 12046853272626645941
15 4141105812465409534
13 14682102426013724743
0 6776354965852488336
2 17317351579400803545
1 9411604119239567138
5 1505856659078330731
3 12046853272626645940
2 4141105812465409533
8 14682102426013724742
*/

当然，从上面的代码中，我们发现，在初步运行时，原始程序的输出是：

1
flag{10632674-1d219-

但上面代码，前面的输出是：

1
1,0,13,7,2,13,9,8,1,11,2,1,5

本该输出13，实际输出6，本该输出7，实际输出3，看这个样子，盲猜存在替换表

下标 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
对应值 0 1 2 ? ? 9 ? 3 4 7 ? 13 ? 6 ? ?

本来让pwn手@lanpesk帮我修改一下二进制文件，将$f$函数输入的参数模$24$就能出flag，他那边通过Hook的方式搞出来了并出了结果。但他立马去忙另一个Pwn题了，没来得及交。

不过在他逆的时候我也想要尝试一下，我注意到前三位是'012'，尝试hexdump一下：

1
2
$ hexdump -C EzFlag | grep "30 31 32"
00002040  00 2d 00 7d 00 30 31 32  61 62 39 63 33 34 37 38  |.-.}.012ab9c3478|

竟然还真找到了！这样的话，那么就得到了整个替换表了：012ab9c3478d56ef

1
2
3
4
5
6
$ hexdump -C EzFlag | grep "00002040"
00002040  00 2d 00 7d 00 30 31 32  61 62 39 63 33 34 37 38  |.-.}.012ab9c3478|

$ hexdump -C EzFlag | grep "00002050"
00002050  64 35 36 65 66 00 01 01  01 00 00 00 01 1b 03 3b  |d56ef..........;|

那这样就简单了，但最后因为把 for(i=0;i<=31;i++) 写成了 range(31)，结果错了几次，最后正确了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
E=[1,
72,
641,
5194,
41619,
333020,
2664229,
21313902,
170511287,
1364090368,
10912723017,
87301784210,
698414273755,
5587314190116,
44698513521005,
357588108168118,
2860704865345023,
22885638922760264,
183085111382082193,
1464680891056657626,
11717447128453261091,
1505856659078330732,
12046853272626645941,
4141105812465409534,
14682102426013724743,
6776354965852488336,
17317351579400803545,
9411604119239567138,
1505856659078330731,
12046853272626645940,
4141105812465409533,
14682102426013724742,]
Tab="012ab9c3478d56ef"
def f(a11):
    v5,v4=0,1
    M=[[0,1],[1,1]]
    M=matrix(Zmod(16),M)
    v=vector([v5,v4])
    v=(M**(a11))*v
    return v[0]
s=""
for i in E:
    s+=Tab[f(i)]
print(s)
#106326741d21909f2914769f60219a24
flag='flag{'
for i in range(32):
    
    flag+=s[i]
    if(i in [7,12,17,22]):
        flag+='-'
flag+'}'
#'flag{10632674-1d219-09f29-14769-f60219a24}'

3.RSA_NestingDoll

看一眼题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
from Crypto.Util.number import *
from tqdm import tqdm
import os

flag=open("./flag.txt","rb").read()
flag=bytes_to_long(flag+os.urandom(2048//8-len(flag)))
e=65537

def get_smooth_prime(bits, smoothness, max_prime=None):
    assert bits - 2 * smoothness > 0
    p = 2
    if max_prime!=None:
        assert max_prime>smoothness
        p*=max_prime
        
    while p.bit_length() < bits - 2 * smoothness:
        factor = getPrime(smoothness)
        p *= factor

    bitcnt = (bits - p.bit_length()) // 2
    while True:
        prime1 = getPrime(bitcnt)
        prime2 = getPrime(bitcnt)
        tmpp = p * prime1 * prime2
        if tmpp.bit_length() < bits:
            bitcnt += 1
            continue
        if tmpp.bit_length() > bits:
            bitcnt -= 1
            continue
        if isPrime(tmpp + 1):
            p = tmpp + 1
            break
    return p

p1=getPrime(512)
q1=getPrime(512)
r1=getPrime(512)
s1=getPrime(512)
n1=p1*q1*r1*s1
assert n1>flag

p=get_smooth_prime(1024,20,p1)
q=get_smooth_prime(1024,20,q1)
r=get_smooth_prime(1024,20,r1)
s=get_smooth_prime(1024,20,s1)
n=p*q*r*s

print(f"[+] inner RSA modulus = {n1}")
print(f"[+] outer RSA modulus = {n}")
print(f"[+] Ciphertext = {pow(flag,e,n1)}")

好家伙，4个因子的RSA。

分析题目得知，对于内层的 $n_1=p_1q_1r_1s_1$，在外层又增加了 $n=pqrs$，其中 $p=2p_1t_1+1$ 也是素数，$t_1$ 是一个 $2^{20}$ 光滑的数字，也就是 $t_1$ 的所有因子都不超过 $2^{20}$，同理，我们可以定义 $q=2q_1t_2+1,r=2r_1t_3+1,s=2s_1t_4+1$。

那么这样的话，我们就可以有：
$$
n=(2p_1t_1+1)\cdot(2q_1t_2+1)\cdot(2r_1t_3+1)\cdot(2s_1t_4+1)
$$
既然四个部分都是素数，那么显然，有
$$
\phi(n)=16p_1q_1r_1s_1t_1t_2t_3t_4
$$
即：
$$
\phi(n)=16nt_1t_2t_3t_4
$$
根据 $a^{\phi(n)}=1$ （其中 $a$ 为任意与 $n$ 互素的数字），那么有 $a^{16n_1t_1t_2t_3t_4}=1$，根据平方差公式，如果我们把后面的 $n_1t_1t_2t_3t_4$ 看成一个整体 $V$，所以：
$$
a^{16V}-1\equiv 0 \pmod n
$$
连续运用平方差公式，有：
$$
(a^{8V}+1)(a^{4V}+1)(a^{2V}+1)(a^{V}+1)(a^{V}-1)=0\pmod n
$$
那么对等号前面的这一部分和 $n$ 求最大公约数，就有可能能够获取 $n$ 的一个非平凡因子。

既然这样，那我可以直接考虑 $a^{V}-1$ 与 $n$ 的最大公约数了，这样还少几项，免得求出来结果和 $n$ 一样了。

但是 $V$ 是多少，我们并不知道，只知道 $V=nt_1t_2t_3t_4$。根据 $t_1t_2t_3t_4$ 均为 $2^{20}$ 光滑，我们干脆设：
$$
K=n_1\left(\prod_{i=3,i\in\mathrm{Prime}}^{2^{20}} i\right)
$$
还好，Python能存下这个 $K$。

那下面的工作就简单了：

1
2
3
4
5
6
7
8
9
n1=...
n=...
K=prod(primes(3,2**20))*n1
import tqdm.notebook
for i in tqdm.notebook.tqdm(range(50)):
    a=(pow(randint(2,n-1),K,n))
    a=gcd(a-1,n)
    if(a-1 and a-n): 
        print(a)

然后收集这些输出结果，看看有没有 $1024$ 位的，如果有那就是 $n$ 的四个素因子之一。当然也可以少收集一点，利用最大公约数的性质，两两求最大公约数进行筛选，筛选出最后1024位的结果。这样我们可以得到四个素数：

1
2
3
4
5
6
7
8
9
P=[125683674223287511199929391424014734219929730761034704505406502077912931068592209654104284639260219630894098113811768247800221516599685450692968168291635183587179180393366902234918272249925075226909925606203146654066671904662060266720143489438375038870205013633219478048203552298398155090726459590174948565779,

135688958085666204636622376874663606060623037984533127554949215373727873563467489694515897900072291984166610384751239950595038402004183706658277547464498952029614078086225311186822818493543473754253851434625753882109758955467109025977046916035650210512394432911014637466491327705680886113441168344937689638007,

165293766534334939537518403759453195904288488398994935384363775961818408937606146233807349218895775310593518934752532377465822265152794712208153366043542043773820629631171441249084911234683946151327476547332689457976842814673079551173773079413119090604879283595442798446423593904593194642805572814867983715659,

171992947779697253514842018906106717097617047303660953087228428161586951197083418557630125796886050555639244757349493198625340520305483122835096327921652178586748527141366322566837087081627360648682493756220339525276499107490885759486958160958806343194124554408371444895822657363164108260683273564115772674159]


然后将这四个 $P$ 减去一的值丢到factordb.com中去分解，找最大的那个素数因子（应该是154~155位十进制数），可以得到：

1
2
3
4
p1=12640586780178354278771080052383497749869399865273557422350740376242446319503391917174055513935117677336547258288132280151433761630655572270163827336131139
q1=12094541303222723616975666632268830751848445571951987169074250626437877110205699058506111384472586354084793914769711672322551034923778729430162356351731919
r1=8032658322599620029480213181968895812810902172967093552713506521436300000398610054134219799747232115213014217973189950145890725588704391460190522209172659
s1=13143792383429631567176338805648361858645034742838692599578815532866468916133309392038207913937396336227239361151049752128445345075961851450420118805042241

那最后就是解密了：

1
2
3
4
5
6
7
8
9
10
e=65537
mod=16141229822582999941795528434053604024130834376743380417543848154510567941426284503974843508505293632858944676904777719167211264225017879544879766461905421764911145115313698529148118556481569662427943129906246669392285465962009760415398277861235401144473728421924300182818519451863668543279964773812681294700932779276119980976088388578080667457572761731749115242478798767995746571783659904107470270861418250270529189065684265364754871076595202944616294213418165898411332609375456093386942710433731450591144173543437880652898520275020008888364820928962186107055633582315448537508963579549702813766809204496344017389879
assert p1*q1*r1*s1==mod
d=inverse(e,(p1-1)*(q1-1)*(r1-1)*(s1-1))
c=657984921229942454933933403447729006306657607710326864301226455143743298424203173231485254106370042482797921667656700155904329772383820736458855765136793243316671212869426397954684784861721375098512569633961083815312918123032774700110069081262242921985864796328969423527821139281310369981972743866271594590344539579191695406770264993187783060116166611986577690957583312376226071223036478908520539670631359415937784254986105845218988574365136837803183282535335170744088822352494742132919629693849729766426397683869482842748401000853783134170305075124230522253670782186531697976487673160305610021244587265868919495629

from Crypto.Util.number import *
long_to_bytes(int(pow(c,d,mod)))
#b'flag{fak3_r5a_0f_euler_ph1_of_RSA_040a2d35}\x7fp\xcb\xd6\x004"A+\x8crj\xead\x1a\x1f\x8e\xe0\xd9\xadO\x99\xe93\xdb\xef\x8b\x080aj\x9b)rk(C\xd3\xa0\x03\xec\x91r3\x03x\xf3\x8b\x94\x14y\x0bW\x11\x0bLd\xd0\x87\xed\r\x90\x8c\xf7}5Lwe\xd9N\xb6\xfd\x92(p}\x18A[0\x116\xa9\xc6\xfdLZ<@\n\x89d\xc6\xe7\x04\xc5)\x81)\x14\x86E\xca]\xd2\x02c\x1a\xadF\xc0\xe2*\x16y\x16\xb4\xf5K\xec\xaf\xe9\xa3\xf3I\xe6a\x94%\xae5Y\xb6\xa7N!\xf79\xca\xe5^cL\x10 \xbe\xfd\x800\'Il\x9b\x86\xd9\xfcd\xd5\x9e\xa9S\x8c\x80\xc1cM\x16`/\x04\xe8\xa7\xea\xbf+\x81Jw-@T\xe9\xeb\x97\x10h$\x8c\xa7\x9bN\x91\x18u.\xe1\t\xc8\xdc\xc4n%\x9d\x0e\x8a\x05T \xc4\xb0m\xde'

最终flag：

1
flag{fak3_r5a_0f_euler_ph1_of_RSA_040a2d35}

9.2025&23 年终总结

23 岁的最后一天，12 月 29 日，聊聊自己这一年的总结。

2025&23 总体来看，好像实现了挺多的，但总感觉其实还有很多可以改进的地方()，自己的CTF二期也终于结束了。

9.1 学业

研一其实课程并不算多，但作为有课的最后一年还是需要简单关注一下。也许是因为自己密码学基础比较好吧，其实两门密码学课程（密码学与安全协议、公钥密码可证明安全）还是混了2个规格化 90+（94,99），然后加上下学期工程矩阵的 87，三门课直接给我冲到了 86.18 的平均分，南京校区应该是RK1 (1/220) 了但好像无锡有人比我高，算了，问题不大。

这么想起来，上一次拿到年级第 1，还是 2015 年 5 月 19？日的初中的月考，好家伙，这就 10 年了是吧。

不过因为导师过于放养，研一时间其实利用的并不怎么好，整体还是非常迷茫的，导致研一科研进度几乎为0，没有论文（虽然其实研一有论文的也并不多）。但最后凭借着CISCN的省奖和密挑的国奖，最后还是混了个1=奖学金（综测RK 14/220，前10%）。然后冲了波国奖，没冲成，但拿到了校级的至善奖。哈哈，不过有就行了，毕竟东南这边竞争对手太强了，搞 AI +导师Push，真碰瓷不过他们 $\mathsf{QAQ}$。

至少从这个综测看来，还是达成了一开始进入前 25% 的目标的，但研二还能不能保持前 25%，这其实就有点难说了。。。。

9.2 CTF

1 月和 2 月主要还是以CTF为主，当时想的是再搞一下CTF，看看能不能做些其他的比赛（但最后才发现，似乎想多了emmm…）。当时只是觉得同源好难，然后很多东西都学得不太懂。在CISCN的半决赛中，由于是AWD赛制，所以做Crypto的只能摆烂（x。不过还好靠着去年的初赛，那个400分的LWE题目，自己也算是有一些贡献的。

然后 3 月和 4 月本来想自己学一点应急响应之类的，但 4 月初被上一届学长学姐开题时什么成果都没有的情况整怕了，那一次开题给自己的感觉就是几个学姐学长开题被隔壁某个组的老师狂怼，然后其他学生，因为导师在这边，所以答辩时老师还能护着一点。可以说，这一次开题给自己造成了非常严重打击，然后CTF就开始减少搞了。加上密挑开始了， 自己就更没怎么继续搞了。。。

9 月因为要给SUSCTF出题，就重新看了一下CTF相关的内容，结合着自己去年打过单独各种比赛，包括网鼎杯、强网杯、CISCN等比赛，当然还有SUSCTF自己做的题目，模仿着出了 10 个备用题。最后根据解题情况上了1,3,4,5,6,7,8七个题。最后解题结果来看，几个稍微难一点的题目至少在当时都没有被AI秒，难度梯度控制得也算是比较好的了。

9.3 密挑

今年最大的一个事情应该就是密挑了。这个比赛其实我在大一的时候就听说过，但是由于当时保研不能算加分，所以当时就没有参加了。一个是20年学长好像是获得了二等奖，然后还有一个是21年当时我这一届另外两个搞Crypto的同学和学长拿了个三等奖，再加上看到了鸡块的博客，去年的密挑似乎是RSA相关的，因此自己决定开始尝试着搞。于是自己在24年第一次组会上，就跟老师说了自己想参加这个比赛的想法，然后刚好自己去年，东大两个学长跟孙老师拿到了二等奖，然后就联系上了孙老师参赛。

今年自己同时参加了赛题一和赛题二，赛题一跟上交一起合作的（用了那边的设备，基本上还是自己一个人根据孙老师的意见编程 + 修改的）。而赛题二由于是孙老师主要的研究方向，自己关注到了G6K、Flatter、Blaster等，并调研了一些有关SVP求集的内容。但在解完了前 5 个题之后，发现后面 3 个题完全不可做。因此转攻赛题一。最后赛题一进了决赛，拿了个全国二等奖，然后赛题二也算混了个赛区二等。当然也和很多其他师傅面基成功。

9.4 和其他师傅的面基

CTF最后一年，那肯定少不了和其他师傅面基的。

8月19日：密挑报道提前和O.O师傅见面，并在比赛结束后的8月21日一起重新逛了逛西安的大唐不夜城、回民街、钟楼，这些地方自己2015年和父母来过一次，但10年后再来，还是有了很多不一样的感觉。

8月20日：在去赛场的车上，面基了糖醋小鸡块、hashhash、yolbby三位大佬，然后到赛场后，见到了东南当年的两位学长rec和oc，在西电认识了oracle师傅（可惜自己的学长随园师傅竟然没去）。比赛结束后跟这些等密码师傅干了个饭。作为一个水平不太行的密码手，能和这些大佬一起干饭是自己的荣幸😋。

10月10日：回南邮玩了一趟（其实是修电脑），见到了Sean学弟。

11月27日：和正规子群的群友 LOV3, m1n9, Troide 在南京面基。

9.5 其他

总体来看，这一年似乎一切都在复刻自己本科3，4，5三个学期，对标2022&20那一年：

2022&20 2025&23
竞赛 2022ciscn (国2=),2022数模美赛(Meritorious) 2025密挑(国2=),2025ciscn(赛区1=)
学业综测 1/230@njupt 14/220@seu
学生活动 C语言急救车@njupt 2025期末复习分享会@seu

不过2025&23和2022&20相比，还是有挺多突破的：这一次真正开始接触科研，慢慢跟着导师做实验，写论文，出差。格密码一些理论知识掌握的更深了，还解锁了一些其他的新技能。因为没加什么学生组织了（以前在南邮还在科协玩），所以很多玩的东西也没了，偶尔在学校图书馆前草坪上躺着确实挺舒服的。

总体来看，2025年和2024年相比，自己确实实现了很多，虽然25年自己确实经历了一些波折吧。但总体来看，目前似乎还是平稳下来了。后面跟着孙老师，好好做，争取再做出一些成就，然后考虑考虑毕业的事情，先把毕业要求达成再说。

2025&23年终总结也就这些了，那就放个倒计时，进入下一年吧。
$$
\mathsf{2025.12.29~~23:59:57} \space\space\space \mathsf {23}
$$

$$
\mathsf{2025.12.29~~23:59:58} \space\space\space \mathsf {23}
$$

$$
\mathsf{2025.12.29~~23:59:59} \space\space\space \mathsf {23}
$$

$$
\mathsf{2025.12.30~~00:00:00} \space\space\space \mathsf {24}
$$

$$
\mathsf{2025.12.29\space\space23:59:59\rightarrow{2025.12.30\space\space00:00:00}}
$$

$$
\huge\mathsf{23(Contest)\rightarrow{24(Research)}}
$$

CTFSeason4
#WriteUp
ciscn2026wp1
http://example.com/2025/12/29/ciscn2026wp1/
作者
huangx607087
发布于
2025年12月29日
许可协议