RSA Notes 2

huangx607087学习RSA的笔记(2)

O-About

一个密码学废物的学习笔记2，很菜，别看。以后会不定时地补充。

约定：此博客中如果出现除法，未特殊说明的，均为向下取整的整除！

I-RSA的乘法的同态性

0x01 简介和 得到$m$的二进制位数

​ CTF中有些题目会在给出$e,n,c$的情况下，允许你和服务器交互，发送你自己的密文$c’$，然后告诉你有关$c’$解密后的明文的一些高位比特信息。在这种时候，我们就需要用到RSA乘法具有同态性的这一特殊性质，那么什么是RSA的同态性呢？

​ 我们已经知道，RSA加密函数$c=E(m) \equiv m^e \mod n$。其中$(e,n,c)$作为公钥，都是已知的。不过我们可以推导一下这样的公式：$E(2m)\equiv 2^em^e\equiv 2^e c\mod n$。所以如果在获得对个人密文的解密权的时候，我们就可以通过向服务器发送$2^e c$，这一就可以获得$2m$的值。同理，我们可以发送$2^{ke}c$，得到的解密结果就是$2^{k}m$。所以运行以下代码，我们得到的结果是$(12,24,48,96)$。

from Crypto.Util.number import *
m=12
p=getPrime(512)
q=getPrime(512)
n=p*q
e=65537
d=inverse(e,(p-1)*(q-1))
c=pow(m,e,n)
print(c)
c2,c3,c4=c*pow(2,e,n)%n,c*pow(2,2*e,n)%n,c*pow(2,3*e,n)%n
print(c2)
m1,m2,m3,m4=pow(c,d,n),pow(c2,d,n),pow(c3,d,n),pow(c4,d,n)
print(m1,m2,m3,m4)

​ 这种方法我们可以确定明文的长度：假如$n$是$2048$位，每次给你最高$8$位，那么被隐藏了$2040$位。假如我们一共移动了$740$位发现高位不再为$0$，那么我们可以确定明文长度为$2040-740=1300$位二进制数。

0x02 RSA确定$m$位数后确定明文$m$的值

​ 假如我们以上面那个为例子，我们确定了明文是$1300$位二进制数，那么我们现在就可以二分了：我们可以设置$L=2^{739},R=2^{740}$进行二分操作。

​ 注意在RSA中，有一个很神奇的式子：
$$
(pm)^e \equiv cp^e \mod n
$$

​ 然后我们可以得到这样的方程：$I=\dfrac {2^{2040}}{m}∈[2^{739},2^{740}]$，也就是$I \in [2×2^{738},4×2^{738}]$。对服务器发送区间中值$M=3×2^{738}$的加密结果乘上$c$的值，如果服务器告诉你最高的$8$位二进制数值不为$0$，则说明我们发送的数字偏大，随后我们就可以换区间右边界$R$为这一次的中值$M$,区间变成$[4×2^{737},6×2^{737}]$。若最后告诉你结果为$0$，那么说明我们发送的值偏小，然后我们可以把左边界换成$M$，然后把区间换成$[6×2^{737},8×2^{737}]$。后面以此类推。

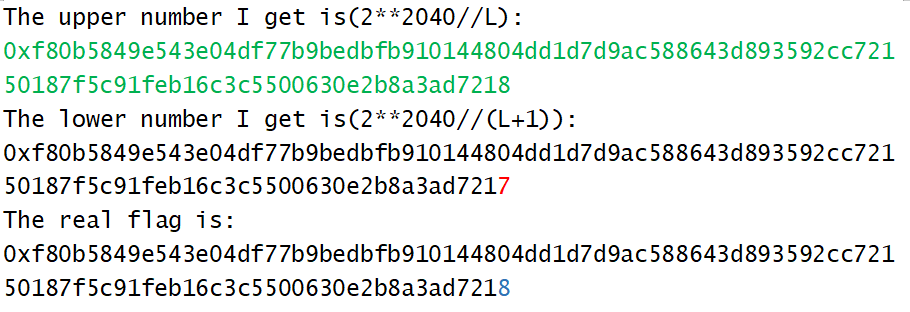
​ 然而，我发现：自己的取值出了一个严重的问题，下面是一次二分过后的运行结果：

​ 分析了一下，原因很简单：因为这个时候除数是$2^{739}$到$2^{740}$左右的数量级，被除数是$2^{2040}$数量级，相差过大，于是我重新造数据：把flag的数量级降低到$2^{400}$,二分的$L,R$数量级提升到$2^{1640}$

​ 这一次的的运行结果，很准确：

​ 做了几次实验，发现flag规模在$2^{1000}$以下的时候无误差，$2^{1050}$规模的flag有不超过$10$的误差，$2^{1100}$规模的flag有几百的误差，$2^{1200}$的flag有几十万的误差，$2^{1300}$的flag的误差比特已经接近总比特数的一半。目测如果flag在$\sqrt{n}$内的话，就不会出现误差值。

最后贴一下测试代码

from Crypto.Util.number import *
import random
def GetNumberBitz(x):
    s=0
    while 1:
        tmp=random.randint(0,255)
        s=s*256+tmp
        if(s>(1<<5000)):
           break
    s=s%(1<<(x+1))
    while(s.bit_length()!=x):
        s=GetNumberBitz(x)
    return s
def GenerateKey(B):
    e,p,q=getPrime(random.randrange(16,20)),getPrime(B//2),getPrime(B//2)
    n,phi=p*q,(p-1)*(q-1)
    d=inverse(e,phi)
    return e,n,d
def judg(CC,D,N):
    x=pow(CC,D,N)
    st=long_to_bytes(x,2048//8)
    if(st.startswith(b"\x00")):
        return 1
    else:
        return 0
def Attack(E,N,C,D,B,T):
    L,R=2**(B),2**(B+1)
    while R-L>1:
        if(R-L).bit_length()%50==0:
            print(hex(L),hex(R))
        M=(L+R)//2
        CC=(pow(M,E,N)*C)%N
        check=judg(CC,D,N)
        if(check==1):
            L=M
        else:
            R=M
    return L
#----main below----#
flag=GetNumberBitz(400)
assert flag.bit_length()==400
e,n,d=GenerateKey(2048)
while n.bit_length()!=2048:
      e,n,d=GenerateKey(2048)
c=pow(flag,e,n)
print('e=',e)
print('n=',n)
print('c=',c)
print('2**2040//flag=',hex(2**2040//flag))
F=Attack(e,n,c,d,2040-400,2040)
print(hex(2**2040//F))
print(hex(2**2040//(F+1)))
print(hex(flag))

0x03 最后一个比特位泄露破解的原理(摘自CTFWIKI，本废物还不懂)

​ 假设目前存在一个 Oracle，它会对一个给定的密文进行解密，并且会给出明文的最后一个字节。那么给定一个加密后的密文，我们只需要 $\log_{256}n$ 次就可以知道这个密文对应的明文消息。

这个其实算作 RSA parity Oracle 的扩展，既然可以泄露出最后一个字节，那么按道理我们获取密文对应明文的次数应该可以减少。

假设$C=P^e \bmod N$

第一次时，我们可以给服务器发送$C*256^e=(256P)^e \bmod N$

服务器会计算得到$256P \bmod N$

这里

• $256P$ 是偶数。
• $N$ 是奇数，因为它是由两个大素数相乘得到。

由于 $P$ 一般是小于$ N$ 的，那么$256P \bmod N=256P-kn, k<256$。而且对于两个不同的 $k_1,k_2$，我们有

$256P-k_1n \not\equiv 256P-k_2n \bmod 256$

我们可以利用反证法来证明上述不等式。同时 $256P-kn$ 的最后一个字节其实就是 $-kn$ 在模 $256$ 的情况下获取的。那么，其实我们可以首先枚举出 $0$~$255 $情况下的最后一个字节，构造一个 k 和最后一个字节的映射表 map

当服务器返回最后一个字节 b，那么我们可以根据上述构造的映射表得知 $k$，即减去了 $k$ 个$N$， 即 $kN \leq 256 P \leq (k+1)N$。

此后，我们使用数学归纳法来获取 P 的范围，即假设在第 i 次时，$\dfrac{xN}{256^{i}} \leq P < \dfrac{xN+N}{256^{i}}$

进一步，在第 i+1 次时，我们可以发送

$C*256^{(i+1)e}$

服务器会计算得到

$256^{i+1}P \bmod N=256^{i+1}P-kN$

$0 \leq 256^{i+1}P-kN<N$

$\dfrac{kN}{256^{i+1}} \leq P < \dfrac{kN+N}{256^{i+1}}$

根据第 $i$ 次的结果

$\dfrac{256xN}{256^{i+1}} \leq P < \dfrac{256xN+256N}{256^{i+1}}$

我们这里可以假设 k=256y+t， 而这里的 t 就是我们可以通过映射表获取的。

$\dfrac{256yN+tN}{256^{i+1}} \leq P < \dfrac{256yN+(t+1)N}{256^{i+1}}$

与此同时，由于 P 必然存在，所以第 i+1 得到的这个范围和第 i 次得到的范围必然存在交集。

所以 y 必然与 x 相等。

进一步我们可以这么归纳，初始情况下

lb = 0
ub = N

假设服务器返回了 b，那么

k = mab[b]
interval = (ub-lb)//256
lb = lb + interval * k
ub = lb + interval

II-关于一些特殊性质的$n$的因数分解

0x01 $n$的值小于$512$位二进制数

​ 可以用yafu或者sagemath直接分解，一般$30$分钟内就可以分解成功

0x02 $p,q$ 是两个相邻的素数

​ 这种方法是非常简单的，我们只需要用gmpy2中的iroot函数直接取整开根。然后设$q$是$\sqrt n$的下一个素数，然后我们就可以得到$p$的值了，进而成功分解$n$

0x03 $|p-q|$过大或者过小的分解

​ $|p-q|$过大的时候，可以直接通过枚举法确定其中一个因数

​ $|p-q|$过小的时候：由基本的平方差公式，有:
$$
\dfrac{(p+q)^2}{4}-n=\dfrac{(p+q)^2}{4}-pq=\dfrac{(p-q)^2}{4}
$$
​ 既然 $|p-q|$较小，那么 $\dfrac{(p-q)^2}{4}$ 自然也比较小，进而 $\dfrac{(p+q)^2}{4}$ 只是比 N 稍微大一点，所以 $\dfrac{p+q}{2}$ 与 $\sqrt{n}$ 相近。

​ 此时我们可以检查$\sqrt n$的每一个整数$x$，知道找到一个$x$使得$x^2-n$是平方数，记作$y^2$。然后根据平方差公式可以分解$n$

0x04 $p-1$光滑(摘自yulige的博客–NCTF2019题解)

0o401 什么是光滑数

​ 首先引入光滑数的定义：若一个数的所有素因子都不超过$B$，那么称这个数为$B$光滑数，例如：由于$72=3^2×2^3$，所有的素因子都不超过$3$，所以$72$是$3$光滑数，当然也是$5,7,11,…$光滑数。

0o402 Pollards $p-1$ 算法

​ 这个时候我们可以使用Pollard’s $p − 1$ 算法来分解 $n$，具体原理如下：

​ 由费马小定理$a^{p-1} – 1 \equiv 0 \mod \ p$可知，$a^{p-1} – 1$ 是 $p$ 的倍数，也就可以认为是$a^{t(p-1)} – 1 =k p$，其中$t,p\in N_+$。因此，简单地观察就可以知道，如果指数$\text{exp}$是 $p-1$ 的倍数，那么$a^\text{exp} – 1 $就会是 $p$ 的倍数。所以，我们只需要找到一个$\text{exp}$使得$a^\text{exp}$是$p$的倍数的时候，那么我们计算$\gcd(a^{\text{exp}},n)$，就可以得到结果，而这个结果就是$p$，所以，这里的关键就是寻找这个合适的$\text{exp}$值。

​ Pollard的厉害之处就在于此，他发现，如果p-1正好是一些很小的质数的乘积，那么p-1就能整除$n!$，其中$n$是一个不太大的数。假设p-1是p1, p2, ..., pk这些质数的乘积，其中最大的质数是pk。那么，很显然pk!=1·2·...·pk肯定包括了p1, p2, ..., pk这些质数的乘积，pk!肯定是p-1的倍数。

​ 也就是说，$n > pk$ 的时候，$n!$很大概率上就能被p-1整除。（考虑到p1, p2, ..., pk中可能有重复的情况）

​ 这导致了Pollard' p-1 method：

​ 对于每一个$n = 2, 3, 4, …$，我们任意选择一个底数$a$（事实上，我们可以简单地选择为$2$），并计算
$$
gcd(a^{n!-1}, N)
$$
​ 如果结果落在1和$n$中间，那么我们就成功了。

​ 当然，这里的所有操作都可以在模$N$的操作下进行，也就是计算$a^{n!-1}\ \text{mod}\ N$。并且，我们也不必计算每一个数字，选择一个恰当的间隔（比如$15$）计算可以减少耗时

0o477 代码实现

​ 我们可以上一下代码：这里的的$N$是$104729$光滑的（因为$104729$刚好是第$10000$个素数）

from Crypto.Util.number import *
def Pollard_p_1(N):
    a = 2
    while True:
        f = a
        # precompute
        for i in range(1, 80000):
            f = pow(f, i, N)
        for i in range(80000, 104729+1):
            f = pow(f, i, N)
            if i % 15 == 0:
                d = GCD(f-1, N)
                if 1 < d < N:
                    return d
        print(a)
        a += 1

0x05 $p+1$光滑(即$p+1=db^2|_{d<256,\text{isPrime}(d)=\text{True}}$)

​ 这种情况下，我们可以使用William $p+1$算法

0o501 理论基础

​ 从标题中我们可以知道：如果$p+1=db^2$ 的话，我们可以考虑分解$n$的值。而这实际上基于这样一个理论基础：如果$n=pm$，并且$p$是素数，并且如果$4p$可以写成集合{$ 3b^2+1,11b^2+1,19b^2+1,43b^2+1,67b^2+1,163b^2+1$} ，其中${b\in N_+}$ 中的任意一个形式，那么我们可以在$\ln n$的复杂度里找到$p$的真实值。

​ 算法的原理太复杂，这里就不多讲了，直接看代码吧（

0o577 算法代码

​ 最后贴一下代码，$\text{Sagemath 9.1 Notebook}$中的代码，摘自$\text{NCTF 2020 WP}$

def qicheng(n: int):
    R = Integers(n)
    js = [0, (-2 ^ 5) ^ 3, (-2 ^ 5*3) ^ 3, (-2 ^ 5*3*5*11) ^ 3, (-2 ^ 6*3*5*23*29) ^ 3]
    p, q = None, None
    for _ in range(20):
        for j in js:
            if j == 0:
                a = R.random_element()
                E = EllipticCurve([0, a])
            else:
                a = R(j)/(R(1728)-R(j))
                c = R.random_element()
                E = EllipticCurve([3*a*c ^ 2, 2*a*c ^ 3])
            x = R.random_element()
            z = E.division_polynomial(n, x)
            g = gcd(z, n)
            if g > 1:
                p = Integer(g)
                q = Integer(n)//p
                break
        if p:
            break
    return (p, q)
print(qicheng(1444329727510154393553799612747635457542181563961160832013134005088873165794135221))
#(74611921979343086722526424506387128972933, 19357894679486057806987068960980789709937)

0x06 Pollord Rho算法(时间复杂度$O(\sqrt[4]{n})$)

0o601 算法介绍

​ 这个算法的核心思想就是猜一个数，看看是否为$x$的因数。

​ 我们可以随机地选取两$v,t$个数，然后根据$v=v_{i-1}^2+t \mod x$ ,这样就会构成一个环。然后在循环内部猜测。即可。

​ 代码实现原理也比较复杂（实际上是因为懒，博客写到后面也很累的），自己百度吧。上一个是百度不到的。23333

0o677 代码实现（自己打的代码，Python常数较大，能过洛谷模板题93分）

from Crypto.Util.number import *
from random import *
A=0
def culc(x,c,n):
    return (x*x+c)%n
def PollardRho(x):
    s,t,goal,val=0,0,1,1
    c=getrandbits(15)%(x-1)+1
    while 1:
        for det in range(1,goal+1):
            t=culc(t,c,x)
            val=val*abs(t-s)%x
            if(det%127==0):
                d=GCD(val,x)
                if(d>1):
                    return d
        d=GCD(val,x)
        if(d>1):
            return d
        goal*=2
        s=t
        val=1
def factor(x):
    global A
    if(x<=A or x<2):
        return
    if(isPrime(x)):
        A=max(A,x)
        return
    p=x
    while(p>=x):
        p=PollardRho(x)
    while((x%p)==0):
        x//=p
    factor(x)
    factor(p)
T=int(input())
while T>0:
    T-=1
    A=0
    a=int(input())
    if(isPrime(a)):
        print('Prime')
    else:
        factor(a)
        print(A)