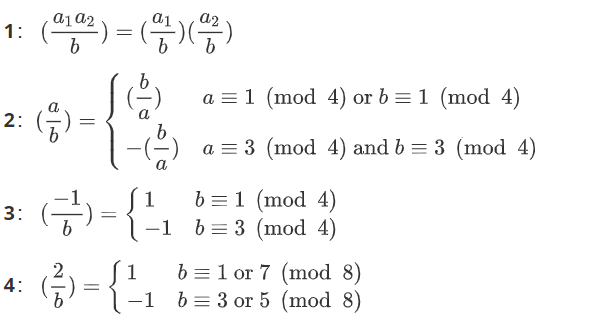NumberTheory3

huangx607087 学习数论的笔记3

1.素性测试&卡米歇尔数

由费马小定理可知： $\text{isPrime}(p)=1 \Rightarrow a^{p-1}\equiv 1 \pmod p$

然而：$a^{p-1}\equiv 1 \pmod p \not\Rightarrow \text{isPrime}(p)=1$

卡米歇尔数就是符合$a^{p-1}\equiv 1 \pmod p $并且$ \text{isPrime}(p)=0$的一类数字，最小的数是$561$，$10000$以内的卡米歇尔数一共有$7$个，分别是$561,1105,1729,2465,2821,6601,8911$

卡米歇尔数的性质 设$C$为卡米歇尔数，$p$是$C$的质因数，则$p^2$不整除$C$，并且$p-1$可以整除$C-1$

根据以上的结论，我们不可以用费马小定理判断一个数是否为素数(虽然准确率很高，但还是有错误率的)，于是我们可以得到下面的素数性质

素数的的性质 2
如果$p$是素数，那么$p$满足以下$2$个条件之一（设$p-1=2^kq$，其中$q$为奇数） 1.$a^q\equiv 1 \pmod p$ 2.$a^q,a^{2q},a^{4q},…,a^{2^{k-1}q}$中至少有一个模$p$结果为$-1\pmod p$

所以，我们就有了以下判断素数的代码，一次误判率低于$0.25$，基本上$30$次的判断准确率就超过了费马小定理了。

from random import *
from os import urandom
from Crypto.Util.number import *
def izprime(p):
    q=p-1
    B=p.bit_length()
    K=0
    while(q&1==0):
        q>>=1
        K=K+1
    print(q,K)
    for i in range(30):
        a=bytes_to_long(urandom(B%700))%p
        if( pow(a,q,p)==1 or pow(a,q,p)==p-1):
            return 1
        E=q
        for j in range(K):
            E=(E*2)%p
            if(pow(a,E,p)==p-1):
                return 1
        return 0
print(izprime(7878787629))

2.二次互反律和有限域开平方

PART 1：二次互反律

二次互反律在 0xGame Div 4 里面有很详细的讲解，这里直接放一下结论。

程序代码如下：

def isqr(x,p):
    if p==1 or x==1:
        return 1
    sgn=1
    while x%2==0:
        x=x//2
        if p%8==3 or p%8==5:
            sgn=-sgn
    if x<p:
        _tmp=p
        p=x
        x=_tmp
        if x%4==3 and p%4==3 :
            sgn=-sgn
    return sgn*isqr(x%p,p)

PART 2：有限域开平方公式[UPD 2021 .2.10,2021.8.5]

解方程$x^2\equiv a \pmod p$，其中$p$是素数，那么开平方有如下公式：

当$p\equiv 3 \pmod 4$时，$x^2\equiv a \pmod p$的一个解为
$$
x=a^{(p+1)/4}
$$
当$p\equiv 5 \pmod 8$时，$x^2\equiv a \pmod p$的一个解为
$$
x=2^{(p-1)/4}a^{(p+3)/8}
$$
这一种情况，也有版本说是$a^{(p+3)/8}$和$2a(4a)^{(p-5)/8}$两个数中的一个。

最困难的就是$p\equiv 1 \pmod 8$的情况了，这个方法没有公式可用。

以下就是完整的有限域开平方的代码了（实际上solve_M8R1这个函数适用于任何素数，但由于其他两类素数已经有公式可用，故这里只用于$p\equiv 1 \pmod8$的情况里）

from Crypto.Util.number import *
from os import urandom
class Complex:
    def __init__(self,x=0,y=0):
        self.real=x
        self.imag=y
def isqr(x,p):
    if p==1 or x==1:
        return 1
    sgn=1
    while x&1==0:
        x>>=1
        if p&7==3 or p&7==5:
            sgn=-sgn
    if x<p:
        x,p=p,x
        if x&3==3 and p&3==3 :
            sgn=-sgn
    return sgn*isqr(x%p,p)
def Rand(p):
    return bytes_to_long(urandom(80))%p
def Cmul(a,b,nr,p):
    Real=a.real*b.real+a.imag*b.imag*nr
    Imag=a.real*b.imag+b.real*a.imag
    Res=Complex(Real%p,Imag%p)
    return Res
def Cpow(a,e,nr,p):
    Res=Complex(1)
    while e:
        if e&1:
            Res=Cmul(a,Res,nr,p)
        a=Cmul(a,a,nr,p)
        e>>=1
    return Res
def solve_M8R1(n,p):
    while 1:
        a=Rand(p)
        nr=(a*a-n)%p
        if isqr(nr,p)==-1:
            break
    Res=Complex(a,1)
    return Cpow(Res,(p+1)//2,nr,p)
def solve(n,p):
    assert isPrime(p)
    A=None
    if n==0:
        return str(0)
    if isqr(n,p)==-1:
        return "No Solution!"
    if p&3==3:
        A=pow(n,(p+1)//4,p)
    elif p&7==5:
        A=pow(n,(p+3)//8,p)
        if pow(A,2,p)!=n:
            A=2*n*pow(4*n,(p-5)//8,p)%p
    elif p&7==1:
        A=solve_M8R1(n,p).real
    return min(A,p-A)
def getQR(p):
    while 1:
        qr=Rand(p)
        if isqr(qr,p)==1:
            return qr
def getNR(p):
    while 1:
        nr=Rand(p)
        if isqr(nr,p)==-1:
            return nr
def getmod8prime(Rem,nbits=100):
    assert Rem in [1,3,5,7]
    while 1:
        p=getPrime(nbits)
        if(p%8==Rem):
            return p
def example():
    for i in [1,3,5,7]:
        p=getmod8prime(i)
        qr=getQR(p)
        print(i,qr,p)
        print(solve(qr,p))
example()
'''
1 564173686680696855894901625202 778582575909658190525427416257
140078267336201622222046402618
3 20669060859351317353915889852 727816416573858078097661465723
130587125639883746397277540316
5 791308279743632016519220848802 1167144785223888272103478393117
544427040026345522165219328929
7 40133816673762059960442044861 635211803801872717209601629487
129389297469578896835881311090
'''

3.$p=a^2+b^2?$

结论1：如果某素数$p$可以表示成两个正整数的平方和， 那么$p\equiv 1 \pmod 4$，反过来也同样成立。

下面用递降法求$a,b$：
首先，写$A^2+B^2=Mp,M<p$
然后，选取$u,v$，使得$u\equiv A \pmod p,v\equiv B \pmod p,u,v,\in [\dfrac{-M}{2},\dfrac{M}{2}]$
我们可以得到$u^2+v^2=A^2+B^2\equiv 0 \pmod M$。从而设$u^2+v^2=Mr,A^2+B^2=Mp$
将上面两个式子相乘，得$(u^2+v^2)(A^2+B^2)=M^2rp$
这个式子经过恒等变形，可以化为$(uA+vB)^2+(vA-uB)^2=M^2rp$
两端同时除以$M^2$，就有$\dfrac{(uA+vB)^2+(vA-uB)^2}{M^2}=rp$
可以证明，$r≤\dfrac{M}{2}$，然后继续递降即可。

关于选取$A,B$时需要的注意点： 我们可以取$x^2\equiv -1 \pmod p$，那么有$A=x,B=1,M=\dfrac{A^2+B^2}{p}$
解方程$x^2\equiv -1 \pmod p$时，我们可以随机选取一个数$t$，然后计算$b\equiv t^{\frac{(p-1)}{4}}\pmod p$。又因为$b^2\equiv(\frac{t}{p})\pmod p$。所以$t$总是有$\dfrac{1}{2}$的成功概率。

下面上一下代码，时间复杂度是$O(\ln p)$级别的，$2048$位的质数用时为$2$秒，运行起来还是很快的。

Update 2021.8.8 将M==1的判断中 return(A,B)中的A,B加上了绝对值，因为我们只讨论正数

from random import *
from os import urandom
from Crypto.Util.number import *
def getA(p):
    assert(p%4==1)
    while 1:
        t=bytes_to_long(urandom(195))%p
        s=pow(t,(p-1)//4,p)
        if(pow(s,2,p)==p-1):
            return s
def getAns(A,B,M,p):
    if(M==1):
        return (abs(A),abs(B))
    u,v=A%M,B%M
    if(u>M//2):
        u-=M
    if(v>M//2):
        v-=M
    assert((u**2+v**2)%M==0 and (A**2+B**2)%M==0 )
    r=(u**2+v**2)//M
    A2=(u*A+v*B)//M
    B2=(-u*B+v*A)//M
    return getAns(A2,B2,r,p)
#------MAIN BELOW------#
p=getPrime(256)
while(p%4==3):
    p=getPrime(256)
A=getA(p)
B=1
assert(A**2+B**2)%p==0
M=(A**2+B**2)//p
Ans,Bns=getAns(A,B,M,p)
Ans,Bns=Ans%p,Bns%p
print('p=',hex(p)[2:])
print('Ans=',hex(Ans)[2:])
print('Bns=',hex(Bns)[2:])
print('The answer is:',(Ans*Ans+Bns*Bns)%p==0)
'''
p= d01bb38ba2700cdbd299f1182d0219cc43a9fd03bcdb9c53b69ea2a38dd3cec1
Ans= e0940478adf7d82d6c27327dbfce631f
Bns= 354b787c45b1c0cf60b30879b3caab70
The answer is: True
'''