RSA Notes 3

huangx607087学习RSA的笔记(3)

O-About

一个密码学废物的学习笔记3，很菜，别看。以后会不定时地补充

为了期末考试，30天的CTF学习都摸了，现在风信子里面的大佬越来越多了，我也变得越来越菜。不过还好，自己的高数过了，寒假没事就可以多搞搞CTF了（哦对，还有英语6级，争取大一下半年过掉）

约定：此博客中如果出现除法，未特殊说明的，均为向下取整的整除！

I-RSA中$\gcd(\phi,e)\not = 1$的情况

0x01 题目背景&引例

NCTF中有一道RSA题目给出了$e,\phi$不互素的情况，这就意味着$e,\phi$的逆元$d$不存在，因此我们也就无法使用常规的方法来分解因式。

为了探讨大数字的一般性结论，我们先从小的数字开始，看一个引例：

在数字极小的时候，我们假设$e=7,p=43,q=29,c=394$是已知的（这种情况下都是给出$p,q$的，并且注意到$p-1,q-1$都是$e$的倍数）。然后我们期望的$m$值是$26$（实际上应该是是未知的）。然后我们用下面的代码做一个先加密再解密的实验：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from Crypto.Util.number import *
e,m,p,q=7,26,43,29
n,phi=p*q,(p-1)*(q-1)
'''
print(pow(m,e,n))
print(phi)
'''
c=394
phi=1176
anses=[]
for i in range(n):
    if(pow(i,e,n)==c):
        anses.append(i)
print(anses)
'''
[18, 26, 73, 114, 155, 157, 163, 200, 201, 244, 276, 287, 288, 308, 327, 329, 331, 374, 416, 421, 491, 501, 503, 534, 566, 577, 588, 636, 675, 679, 706, 714, 722, 781, 824, 851, 867, 878, 888, 972, 975, 996, 1023, 1062, 1146, 1168, 1187, 1230, 1233]
'''

然后我们可以发现：当我们尝试用枚举法（反正数字小）尝试枚举符合条件的答案时，发现一共有多解（并且解的个数恰好是$7^2=49$）：我们期望的$26$只是其中的一个解。然而这里也仅仅时在数字较小的时候采用枚举法，我们必须要找到一种办法来真正地来解决这个问题。

0x02 有限域内开根

2o01 Introduction

基础的数学早已告诉我们，$n$次方程有$n$个根。所以当$p-1$和$e$不互素时，$x^e\equiv a \pmod p$要么有$e$个根，要么没有根（这个很容易理解，$e=2$时，方程$x^2\equiv a\pmod p$如果$a$是模$p$二次剩余就有两个根，$a$不是模$p$的二次剩余就没根。）

所以，我们就需要求出在有限域内开$e$次根号，在这里我们无需考虑无解的情况（因为在RSA中，显然有一个解是$m$）

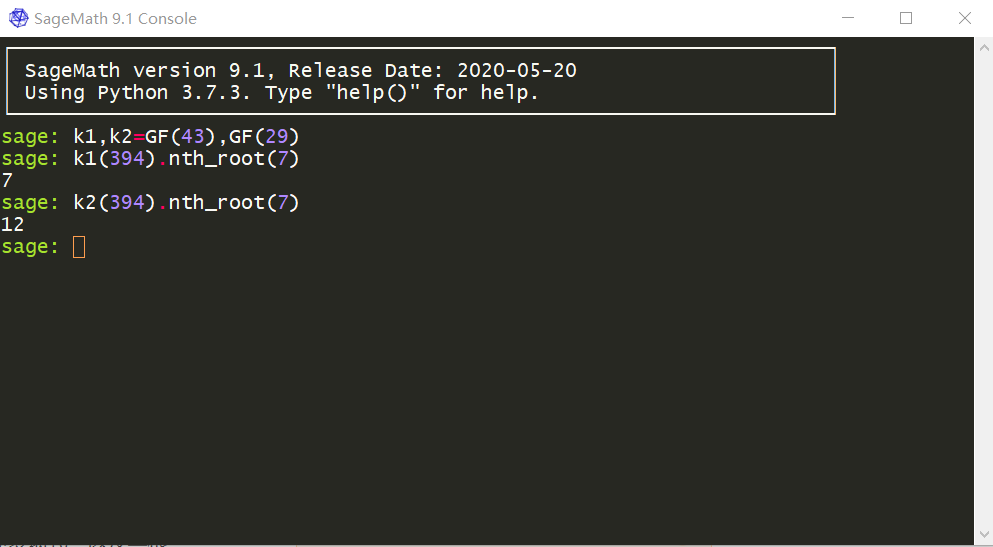
发现$p-1,q-1$都是$e$的 倍数后，我们可以利用sagemath，求出这$e(=7)$个根中的其中一个根，如下图

Picture2o01

至于剩下的$6$个根，我们可以有这样的推导（仍然是以$e=7$为例）：$x=(\sqrt[7]{1×x})^7=(\sqrt[7]1)^7×(\sqrt[7]{x})^7$。可能某些无理数在模意义下不存在，但是这没有关系，因为$x^7\equiv 1 \pmod {43}$绝对不止$1$一个根，比如$41^7\equiv 1 \pmod {43}$。我们可以用下面的脚本求出来，原理见Am4dalao博客中的网页链接

Upd 2021.1.17

用以下sagemath代码求特解更快（$e>4200$的情况下）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
import random
def AMM(o, r, q):
    print('\n----------------------------------------------------------------------------------')
    print('Start to run Adleman-Manders-Miller Root Extraction Method')
    print('Try to find one {:#x}th root of {} modulo {}'.format(r, o, q))
    g = GF(q)
    o = g(o)
    p = g(random.randint(1, q))
    while p ^ ((q-1) // r) == 1:
        p = g(random.randint(1, q))
    print('[+] Find p:{}'.format(p))
    t = 0
    s = q - 1
    while s % r == 0:
        t += 1
        s = s // r
    print('[+] Find s:{}, t:{}'.format(s, t))
    k = 1
    while (k * s + 1) % r != 0:
        k += 1
    alp = (k * s + 1) // r
    print('[+] Find alp:{}'.format(alp))
    a = p ^ (r**(t-1) * s)
    b = o ^ (r*alp - 1)
    c = p ^ s
    h = 1
    for i in range(1, t):
        d = b ^ (r^(t-1-i))
        if d == 1:
            j = 0
        else:
            print('[+] Calculating DLP...')
            j = - dicreat_log(a, d)
            print('[+] Finish DLP...')
        b = b * (c^r)^j
        h = h * c^j
        c = c ^ r
    result = o^alp * h
    return result
print(1)
p=
q=
n=p*q
c=
phi=(p-1)*(q-1)
cMp=c%p
cMq=c%q
print(AMM(cMp,4919,p))
print(AMM(cMq,4919,q))

2o77Code

代码还是要上一下的，帮助理解，万一真有人看不懂原理呢？（我相信是不存在的）

使用urandom的原因是因为虽然这道题的数字小，但以后的数字可能会很大，并且$\mathrm{get}(x,B)$中的$B$在$x$较大的时候也可以$40$换成更大的数字（例如$400$），如果数字太大可以使用文件输出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from Crypto.Util.number import *
from os import urandom
def getx(p,B):
    x=bytes_to_long(urandom(B))%p
    while(x==0):
        x=bytes_to_long(urandom(B))%p
    return x
#------MAIN BELOW------#
n,p=7,29
assert (p-1)%n==0
rem=n
anses=[]
while rem:
    x=getx(p,40)
    g=pow(x,(p-1)//n,p)
    #print(g,pow(g,2*n,p))
    if(pow(g,n*4,p)==1 and g not in anses):
        anses.append(g)
        rem=rem-1
print(anses)     
'''
7th_root_of_1_under_condition_of_n,p=7,43:[35, 4, 41, 16, 21, 11, 1]
7th_root_of_1_under_condition_of_n,p=7,29:[1, 7, 25, 24, 16, 23, 20]
A_7th_root_of_394_under_condition_of_n,p=7,43:7
A_7th_root_of_394_under_condition_of_n,p=7,29:12
'''

我们以$n,p=7,43$的一组解为例：$[35,4,41,16,21,11,1]$一共有七个数字，这七个数字都满足$x^7\equiv 1 \pmod {43}$。然后我们注意一下我们刚才得到的一个数字值$7$。只要我们对这里面的数字每一个都乘上$7$，得到的数列为$[30, 28, 29, 26, 18, 34, 7]$,那么就有了$x^7\equiv394\pmod {43}$，注意到$7^7\equiv 394 \pmod{43}$，因此我们可以姑且地说$\sqrt[7]{394}\equiv 7 \pmod {43}$。$n=7,p=29$的情况也同理。

0x03：求根后两两组合，使用CRT

然后，我们回顾刚才的过程，$m\equiv \sqrt[e]{c} \pmod p,m\equiv \sqrt[e]{c} \pmod q$，一定要注意到由于模数的不同，两个$\sqrt[e]{c}$的值是不一样的，前者我们求出来的$\sqrt[7]{394}$是$[30,28,29,26,18,34,7]$，因为这是模$43$的意义下的数组。后者是模$29$意义下的数组。

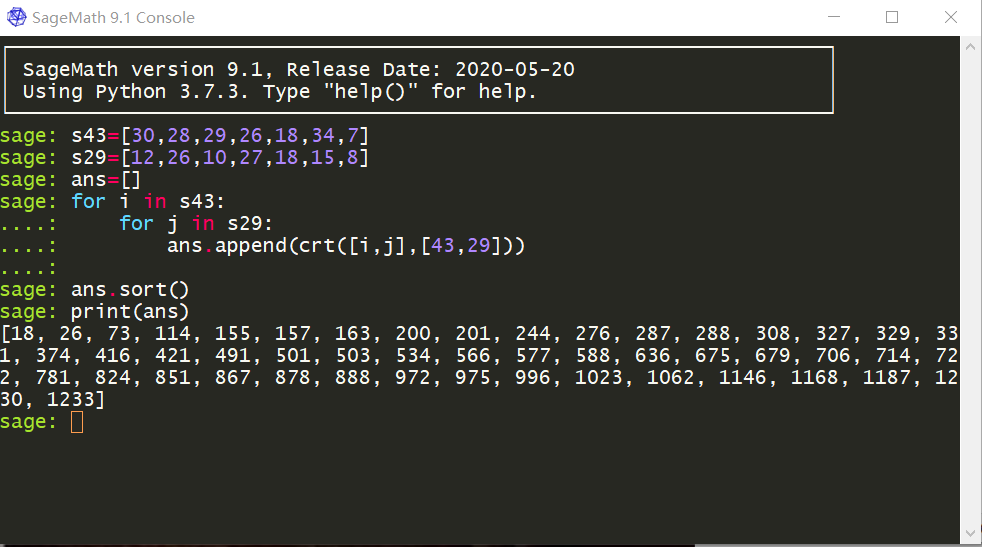
然后，我们可以把结果两两组合（组合定律告诉我们一共有$e^2$种方案），下面分别使用sagemath和python做的情况。

3o01：Sagemath截图

3o01p1

3o02 python代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from Crypto.Util.number import *
def crt2(m1,m2,r1,r2):
    M=m1*m2
    t1,t2=inverse(m2,m1),inverse(m1,m2)
    return (r1*t1*m2+r2*t2*m1)%M
#------MAIN BELOW-----#
s43=[35, 4, 41, 16, 21, 11, 1]
s29=[1, 7, 25, 24, 16, 23, 20]
ans=[]
p43=7
p29=12
for i in range(7):
    s43[i]=s43[i]*p43%43
    s29[i]=s29[i]*p29%29
print(s43)
print(s29)
for i in s43:
    for j in s29:
        ans.append(crt2(43,29,i,j))
ans.sort()
print(ans)
'''
s43=[30, 28, 29, 26, 18, 34, 7]
s29=[12, 26, 10, 27, 18, 15, 8]
ans=[18, 26, 73, 114, 155, 157, 163, 200, 201, 244, 276, 287, 288, 308, 327, 329, 331, 374, 416, 421, 491, 501, 503, 534, 566, 577, 588, 636, 675, 679, 706, 714, 722, 781, 824, 851, 867, 878, 888, 972, 975, 996, 1023, 1062, 1146, 1168, 1187, 1230, 1233]
'''

观察观察，是不是最后的结果与我们一开始枚举求解的结果一模一样？（为了观察方便，特此对ans数组排了个序）

0x04： 最后微调，得出答案

当我们得到$49$个解之后，我们可以根据题目的需要，将解筛选出来，因为在真正的CTF比赛中，flag都是有一定格式的，本题中由于仅仅是从数论的方法来讲解，并且数字较小，所以就讲了个方法，筛选是很容易的，YS9X！

0x05： 总结一下知识点

1：解方程$x^e\equiv a \pmod p$，其中$p$为素数，那么当$\gcd(e,p-1)=1$时，该方程有唯一解，为$a^d$，其中$de\equiv 1 \pmod p$。如果$\gcd(e,p-1)\not = 1$，那么方程最多可以有$\gcd(e,p-1)$个解。

2：当$\gcd(e,p-1)\not =1$时。定义方程$x^e\equiv a \pmod p$中，当$a=1$时为齐次有限域指数方程（我自己定义的），当$a\not = 1$时为非齐次有限域指数方程。齐次有限域指数方程的通解（应该说是所有解）可以用上面的python代码直接求出，非齐次有限域指数方程可以利用sagemath求出方程的一个特解$x_0$。然后用$x_0$乘上对应齐次方程的通解，那么就得到了非齐次方程的通解（实际上我刚才说的是一种很不规范的说法，只不过是为了类比线代和高数才这样姑且地定义的）。

II- 已知$dp,dq,p,q,c$时求解$m$

0x01

一些过于基础的算式我就不给了，我们可以得到这样的两个式子：$dp\equiv d \pmod {p-1},dq\equiv d \pmod {q-1}$

然后我们可以计算$m_1\equiv c^d \pmod p,m_2\equiv c^d \pmod q$

等式经过变形，可以得到$m_2\equiv (kp+m_1)\pmod p$

然后两边同时减去$m_1$，又有$(m_2-m_1)\equiv kp\pmod p$，即$k\equiv p^{-1}(m_2-m_1) \pmod q$

又因为$m=c^d= kp+m_1$，所以$c^d=(p^{-1}(m_2-m_1)\mod q)×p+m_1$

利用$m_1\equiv c^{dq\mod (q-1)} \pmod q,m_2\equiv c^{dp\mod (p-1)}\pmod p$

就可以直接求出答案了，直接上代码，不多说了。

1
2
3
4
5
6
7
8
9
10
11
12
13
from Crypto.Util.number import *
import libnum
p = 
q = 
dp = 
dq = 
c = 
invq=inverse(p,q)
mp=pow(c,dp,p)
mq=pow(c,dq,q)
m=((mp-mq)*invq%p)*q+mq
print(m)

CTFSeason2
#Notes
RSA Notes 3
http://example.com/2021/01/13/RSA-Notes3/
作者
huangx607087
发布于
2021年1月13日
许可协议