LatticeNotes1

Notes
CTFSeason2
发布日期:   2021-02-01

huangx607087学习格密码的笔记1

0.About

一个密码学fw的学习笔记，别看，很菜的。

校内同级某人早就对这一方法有过较为深入的了解，而进入了2月才刚刚开始学习，一下子就比别人慢了半个月，或许自己就算4月进了校队，也无法跟那家伙拼吧（，算了，还是先保住自己目前4.24的GPA吧。因为我是个学术废物和密码学废物

1.引入内容（Known -> Unknown）

1x01 简介

​ 众所周知，公钥密码学的安全性，往往建立在数学问题的困难性上。如 RSA 基于大数分解的困难性，DH 和 Elgamal 以及 ECC，是基于有限域上求离散对数的困难性。我们接下来要考虑一类新的难题，它们支撑了格（lattice）密码学。

　　对比起之前的公钥密码学体系，格密码提供了许多优势：首先，加密、解密速度可以更快（RSA 慢得难以忍受）；可以抵抗量子攻击。目前来看，暂且没有量子算法可以高效解决 lattice 难题。

在谈到格之前，我们先进行一些引入工作：

​ 线性代数中讲过，在实数集$R$上有向量空间$V$,其中向量空间$V$是一部分向量的集合，并且任意两个向量相加，或者是某个向量的数乘，在$V$中仍然有意义。比如，假定$\vec{a},\vec{b} \in V$，则$\vec{a}+\vec{b},2\vec{a}$仍然在向量空间$V$内。

​ 而格实际上就与向量空间相似，不过对于格中的向量的数乘，我们仅限于乘上整数。

1x02 引例——一个新的密码系统

​ 我们先来看一个很简单的问题，而这个问题也开始与一个维度为$2$的格有所联系了。不过由于维度很低，它的安全性很弱，但它可以作为一个很恰当的引例，因为它可以说明如何在密码分析中出现晶格，即使潜在的硬问题似乎与晶格无关。 此外，它还提供了NTRU公钥密码系统的最低维介绍。

​ 加密开始，Alice先选择一个大的正整数$q$（不一定是素数）为一个公共参数作为公钥，并选择两个秘密的正整数$f,g$作为私钥，其中$f<\sqrt{\dfrac{q}{2}},\sqrt{\dfrac{q}{4}}<g<\sqrt{\dfrac{q}{2}}$且$\gcd(f,q)=1$。

​ 然后，Alice可以计算$h\equiv f^{-1}g\pmod q$。我们可以注意到$f,g$都小于$\sqrt q$，也就是说$f,g$的数量级是$O(\sqrt q)$的级别。而$h$的范围则是$O(q)$，在$q$很大的时候（比如$q>2^{256}$）时，$h$可以说是远大于$f,g$的。这个$h$也将作为公钥。随后，Alice将公钥$q,h$公开。

​ 作为信息发送方，Bob对信息加密的时候，也需要用到$2$个参数：明文$m$和一个随机数$r$，其中$m<\sqrt{\dfrac{q}{4}},r<\sqrt{\dfrac{q}{2}}$。然后他就可以计算密文$c\equiv rh+m \pmod q$。

​ 而收到密文后，Alice的解密过程如下：首先，他计算$a\equiv fc \pmod q$和$b\equiv ad \pmod g$，其中$d$是$f$在模$g$意义下的逆元。而神奇的是，对于$a= fc=frh+fm=frf^{-1}g+fm=rg+fm$。然后，我们可以得到$b=ad=drg+dfm\equiv dfm \pmod g$。又因为$df\equiv 1 \pmod g$，所以我们最后算出来的$b=m$就成立了。

我们可以用Python的代码尝试一下整个加密和解密的过程。我们以 $q=1000170007,f=19653,g=18557$为一组测试数据试试看

首先，准备阶段计算$h\equiv f^{-1}g\pmod q=999304853$,这个数字达到了$O(q)$的级别,对外公布$q,h$

加密方设置明文为$m=12345$，选取随机数为$r=20932$，计算$c\equiv rh+m=893838950$。

解密方收到$c$之后，计算$a\equiv fc \pmod q=631051409$。然后计算$d\equiv f^{-1}\pmod g=10887$。

最后计算$b=da=10887×631051409=6870256689783\equiv 12345 \pmod g$，最终获得了明文为$12345$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from Crypto.Util.number import *
from gmpy2 import *
from os import urandom
#PREPARE
q=1000170007 #sqrt(q/4),sqrt(q/2)=15812,22362
f,g=19653,18557
assert GCD(q,f)==1 and GCD(f,g)==1
h=g*inverse(f,q)%q
print(q,h)
#ENCRYPT
m,r=12345,bytes_to_long(urandom(80))%(iroot(q//2,2)[0]-10)
c=(r*h+m)%q
print(c)
#DECRYPT
a=f*c%q
d=inverse(f,g)
b=a*d%g
print(b)
#1000170007 999304853
#893838950
#12345

1x03 对1x02中密码系统的攻击

很显然，由于$f,g$的数量级均为$O(\sqrt q)$，因此暴力枚举的的复杂度是$O(q)$。不过我们可以换一种思路来分析这个问题：攻击者的任务就是找到一组数量级$O(\sqrt q)$的数字$F,G$满足$Fh\equiv G\pmod q$。这个时候$(F,G)$就很可能会充当解密密钥。将刚才的同余式写成方程的形式，也就是$Fh=G+Kq$。也就是$Fh-Kq=G$。根据线性代数的相关知识，我们可以构建这样的式子：$F(1,h)-K(0,q)=(F,G)$。也就是写成了向量加减的形式。其中$\vec a=(1,h),\vec b=(0,q),\vec d=(F,G)$。这个时候，我们就可以构建一个二维的格$L={ A\vec a+B \vec b| A,B\in Z}$。然后在$L$中寻找向量即可。而这个方法也是非常简单的，故上面这个密码体系很容易就能被攻破了。

2.子集问题和背包密码系统

2x01 引入

作为一个早已退役OIfw$\text{(NOIP 2018 245pts)}$，对于$0,1$背包问题是非常熟悉的。不过这里的一个背包密码系统，也可以类比我以前的相关知识：

给你一个数集$M={a_1,a_2,a_3,\dots,a_n}$和一个整数$b$，在集合中$M$选取一个非空子集$M_0$，使得$(\sum _{i \in M_0} i)=b$。

举个例子，比如$M={4,5,12,15,17},b=24$。很显然我们可以选取$M$的子集$M_0={4,5,15}$，这样$M_0$中所有元素之和就等于$24$了。并且这是一个唯一的选法。当然，如果当我们把需求从$24$改成了$32$那么$M_0={5,12,15}$，也可以选取$M_0={15,17}$。这样就有两种选法了。

当然，这个子集问题，也可以采用线性代数的方法来解决。我们只需要构造一个方程$\sum _{i=1}^n a_ix_i=b$即可，其中$x_i\in{0,1}$。如果在已知$M$和$b$的情况，这个算法的复杂度是$O(2^n)$，因为我们可以设向量$\vec X=(x_1,x_2,\dots,x_n)$，$\vec X$是一个$n$维向量，每个分量取值为$0$或者$1$。当然，有一种方法，可以将指数减半，这样算法复杂度就变成了$1.4143^n$

具体做法如下：

首先，假设$M$集合中的数是一个递增序列，那么我们可以将这个集合切成两半，然后枚举所有的集合$I$为集合${a_1,a_2,…,a_{n/2}}$的子集，和枚举所有的$J$为集合${a_{n/2+1},a_{n/2+2},…,a_n}$的子集。并分别列出列表$A,B$分别对应所有$I$的元素之和和所有$J$的元素之和。如果存在某个$I$和某个$J$使使得这两个集合中所有元素之和等于$b$，那么我们就解决了这样的一个问题。而这，也是一个典型的中间人攻击的例子。

这个工作的时间复杂度为$O(2^{n/2})=O(1.4143^n)$，明显是快于原方法$O(2^n)$的。

然而，这里对于任何人来说，解密的复杂度都一样，均为$O(1.4143^n)$。即使是真正的解密者，也不会有所谓的$\text{Trapdoor Infomation}$能够快速出解，那么能不能构造一个所谓的$\text{Trapdoor Infomation}$使得持有私钥的人快速解密呢？

2x02 超级递增序列

下面我们引入一个超级递增序列的概念：就是对于这个集合中的每一个数，前一个数都大于等于上一个数的$2$倍，那么这个序列就可以被称作超级递增序列。比如：$(1,3,9,27,81,243,729)$和$(1,5,13,44,118,395,806)$都满足条件，因此这两个序列均为超级递增序列。

超级递增序列有个性质，就是第$i$个数大于他前面所有数字之和。那么这个时候，我们可以使用贪心算法，在$O(n)$的线性复杂度里算出密钥，具体做法如下。

假定我们选定的序列为$M=(1,3,9,27,81,243)$，$b=91$，那么我们可以使用这样的方法计算：首先，我们发现$81<91<243$，那么我们从序列第$5$位开始，计算$b-a_5=91-81=10$，所以解密密钥$x_5=1$。然后，我们发现$9<10<27$，这个时候我们直接计算$10-9=1$，解密密钥$x_3=1$，最后的$1-1=0$，所以解密密钥$x_1=0$，因此，我们可以得到解密密钥为$\vec X=(1,0,1,0,1,0)$。

但是这样，攻击者也可以通过相同的方法，快速破解这个密钥。

2x03 一个新的公钥密码体系Merkle -Hellman Algorithm

MH-A算法是基于超级递增序列子集问题的一个公钥密码学体系，它使用同余进行伪装，然后通过创建公钥对和私钥对完成加密和解密的一系列操作。

首先，Alice创造一个超级递增序列$\vec R=(r_1,r_2,…,r_n)$和$2$个大整数$A,B$满足$B>2r_n,\gcd(A,B)=1$。然后Alice创造一个新的序列$\vec M=(m_1,m_2,…,m_n)$，使得$m_i \equiv Ar_i \pmod B$，并公开$M$，作为公钥。

Bob收到密钥之后，设明文为$\vec X$，其中$\vec X$是一个$n$维向量，每个分量取值为$0$或$1$。然后Bob计算$C=\vec X ·\vec M$完成加密。

Alice收到密文后，只需要计算出$D=A^{-1}C \pmod B$，然后求$D$在集合$\vec R$ 中的一个表示方法$\vec Q$即可解密。

简单证明一下$\vec Q=\vec X$

由于$D\equiv A^{-1}\sum_{i=1}^{n} x_im_i \equiv A^{-1}\sum_{i=1}^{n} Ax_ir_i \equiv \sum_{i=1}^{n} x_ir_i\pmod B$。而又有$B>2r_n$，因此$D$就是$\vec X ·\vec R$的真实值

下面上一下代码：为了简单，我们以$5$维向量为例：假设$\vec R=(2,5,13,34,87),A=100,B=227$，那么根据Alice的计算，可得$\vec M=(200,46,165,222,24)$。

然后Bob设定的密文$\vec X=(1,1,0,1,0)$，计算$C=\vec X·\vec M=468$作为密文。

Alice根据Bob的密文$C=468$，计算$D\equiv A^{-1}C\equiv 84×468 \equiv 41 \pmod {227}$。

然后将$D$用$\vec R$中的元素进行$0,1$表示，即可还原明文$\vec X$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
from Crypto.Util.number import *
from gmpy2 import *
from os import urandom
#PREPARE
R,A,B=[2,5,13,34,87],100,227
assert GCD(A,B)==1
assert B>R[len(R)-1]
for i in range(1,len(R)):
    assert R[i]>=2*R[i-1]
M=[]
for i in R:
    M.append(A*i%B)
print(M)
#ENCRYPT
X=[1,1,0,1,0]
C=0;
for i in range(len(R)):
    C+=X[i]*M[i]
print(C)
#DECRYPT
D,t=C*inverse(A,B)%B,len(R)-1
print(D)
Q=[0 for i in range(len(R))]
while D and t+1:
    if(D>=R[t]):
        Q[t]=1
        D-=R[t]
    t-=1
print(Q,Q==X)
'''
[200, 46, 165, 222, 74]
468
41
[1, 1, 0, 1, 0] True
'''

2x04 对2x03中加密系统的攻击

2x03中我们提到的密码体系又称作子集公钥密码学系统或者背包密码学系统。其核心思想是生成一个超级递增序列，然后用模线性运算进行混淆，将混淆之后的序列作为公钥。

然而，这一密码系统也有比较大的缺点。由于$M$是一个$n$个整数的列表，每个整数有$2^n$比特长。明文的长度是$n$，密文的长度是$2n$。因此这算是一个$2-\text{to}- 1$的密码体系。当$n=160$时，整个公钥的大小大约是$51200$位以上，远远超过了RSA,ECC等使用广泛的公钥密码系统，不过这个算法由于乘幂和取模较少，因此加密速度也远快于RSA和ECC，因此这一性质也成为了一个比较吸引人的研究点。

然而，如果我们想要获得一个$300$位，比较安全的背包密码学系统，那么整个私钥空间将超过$180\text{KB}$。因此，理论上安全的背包密码基本不存在。

而攻击者想要用向量重新计算子集的问题，那么攻击者就要从$M$中写出$S$的子集和，那么攻击者就可以形成一个这样的矩阵，其中$b=C$，$\text{ones}=(1,1,1,…,1)$，$E$为$n$阶单位矩阵，$M$改写成列向量的形式

1

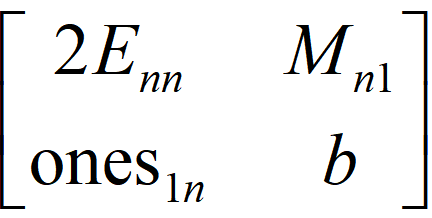
在上面的例子里，我们的矩阵就是这个样子的：

2

把矩阵分离出行向量，那么就有$\vec v_1=(2,0,0,0,0,200),\vec v_2=(0,2,0,0,0,46),\vec v_3=(0,0,2,0,0,165),\vec v_4=(0,0,0,2,0,222),\vec v_5=(2,0,0,0,2,74)$

然后还有一个附加向量$\vec w=(1,1,1,1,1,468)$

然后，我们就可以构建这样一个格$L$，以${v_1,v_2,v_3,v_4,v_5,w}$为基底。那么很显然，$\vec{t}=\sum_{i=1}^5(2v_i-w)=(2x_1-1,2x_2-1,2x_3-1,2x_4-1,2x_5-1,0) \in L$。由于所有的$x$的取值只有$0$和$1$。那么向量$\vec t$的出最后一个分量为$0$外均为$±1$.。我们可以得到$||\vec t||=O(\sqrt n)$。而这个格中的向量，长度都达到了$O(4^n)$，所以向量$ \vec t$可以被认为是一个短向量。

所以，攻击者只需要找到格中的一个最短的非$0$向量，那么就可以恢复明文。

在格中找到短向量的算法称为格减算法。 其中最著名的是LLL算法

2x05 LLL算法的初步实现 in Sagemath

3

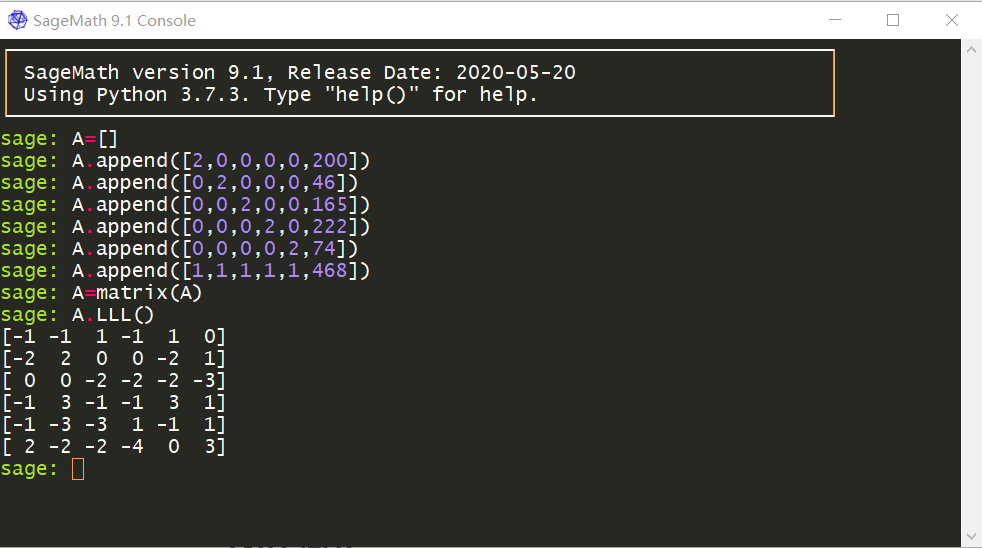
可以看到，第一行向量是$(-1,-1,1,-1,1|0)$，取相反向量得$(1,1,-1,1,-1|0)$，加上$1$然后除以$2$，得$(1,1,0,1,0|0)$，所以通过LLL算法，我们很快就得到了答案为$(1,1,0,1,0)$。

Update 8.30

实际上，这边还有更好的一个矩阵构造方法如图：

也就是上面的分块矩阵中：$2E$改成$E$，$\mathrm{ones}$改成$\vec 0$，$b$改成$-b$后，结果是一模一样的。

4

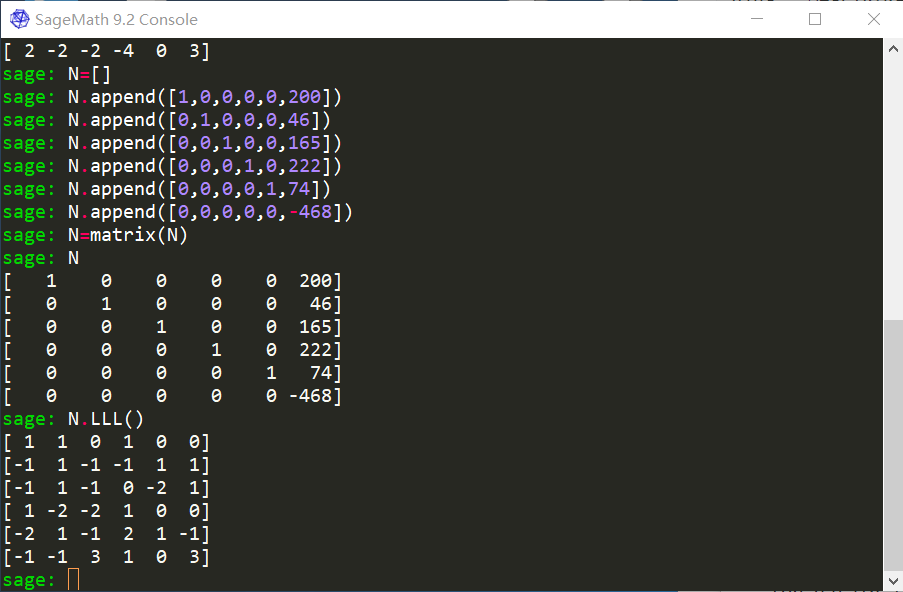
用这个方法，可以直接得到答案为$(1,1,0,1,0)$，不需要对数据进行第二步的处理。

后面对于LLL算法还会有更多笔记，此处仅仅是提及一下，后面的笔记会详细讲解。

文章作者: huangx607087
文章链接: http://example.com/2021/02/01/LatticeNotes1/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 huangx607087 !
Notes
赏
  目录