LatticeNotes2

huangx607087学习格密码的笔记2

0. About

一个密码学fw的学习笔记，别看，很菜的。

这个笔记接着之前发布的笔记1，继续往后面扩展新的内容。

3. 预备知识2：向量空间

1.定义：向量空间是一组向量的集合，这些向量满足加法与数乘的封闭性。也就是对于任意的向量$\vec a ,\vec b \in V$，都有$\vec a+\vec b \in V$，$\lambda\vec a \in V(\lambda \in R)$。

2.线性无关：有$n$个向量，满足$a_1\vec v_1+a_2 \vec v_2+…+ a_n \vec v_n= \vec 0$。若可以找到一组不全为$0$的实数使这个等式成立，那么我们就说$v_1,v_2,…,v_n$线性相关。否则$v_1,v_2,…,v_n$线性无关。

3.基底若$V$中有一组线性无关的向量$v_1,v_2,…,v_r$，那么当这$r$个向量是$V$中的一组基底时，任何一个向量$w \in V$都可以用$v_1$到$v_r$线性表示且表示方法唯一。而基底也一般可以被认为是一个极大线性无关组。

若$V$中有一组基底$v_1,v_2,…,v_n$，如果还有一组向量$w_1,w_2,…,w_n$也可以作为$V$的基底。那么可以推出，每个向量$w$都可以用$v_1$到$v_n$表示，且将表示系数写成矩阵，该矩阵的行列式不为$0$。

4.向量的长度、两向量夹角、向量的数量级内容略去，比较基础，高中的知识直接类比过来就可以了，当然大学的线性代数也是有的。

5.向量的标准正交基：如果有一组向量$e_1,e_2,…,e_n$是向量空间$V$的一组标准正交基，那么有$e_i·e_j=0(i \not =j)$和$|e_i|=1$

6.施密特正交化方法

不知道的自行百度去，我直接上个C++代码走人，讲起来+证明耗费的篇章太大了。

#include<bits/stdc++.h>
using namespace std;
int n,m;
double a[70][70],b[70][70];
double len(double v[],int dim)
{
	int i,j;
	double A=0;
	for(i=1;i<=dim;i++)
		A+=v[i]*v[i];
	return sqrt(A);
}
double mul(double v[],double w[],int dim)
{
	int i,j;
	double A=0;
	for(i=1;i<=dim;i++)
		A+=v[i]*w[i];
	return A;
}
int main()
{
	int i,j,k;
	scanf("%d%d",&n,&m);
	for(i=1;i<=n;i++)
		for(j=1;j<=m;j++)
			scanf("%lf",&a[i][j]);
	memcpy(b[1],a[1],sizeof(a[1]));
	for(i=2;i<=n;i++)
		for(j=1;j<i;j++)
		{
			memcpy(b[i],a[i],sizeof(a[i]));
			double tmp=mul(a[i],b[j],m)/mul(b[j],b[j],m);
			for(k=1;k<=m;k++)
				b[i][k]-=tmp*b[j][k];
		}
	for(i=1;i<=n;i++)
	{
		double l=len(b[i],m);
		for(j=1;j<=m;j++)
			b[i][j]/=l;
	}
	for(i=1;i<=n;i++)
	{
		for(j=1;j<=m;j++)
			printf("%7.4lf ",b[i][j]);
		puts("");
	}
	return 0;
}
/*
3 4
1 6 2 4
5 3 3 -5
6 3 2 -4
 0.1325  0.7947  0.2649  0.5298
 0.5934  0.2516  0.3290 -0.6902
 0.6193  0.4630 -0.2389  0.5874
*/

4.格的基本定义与性质

格的定义：设向量$v_1,v_2,…,v_n$是一组线性无关的向量，那么格就是由这$n$个向量的线性组合集，写成通解的形式就是
$$
\vec w=a_1\vec v_1+a_2\vec v_2+…+a_n\vec v_n| a_i \in Z
$$
其中，$v_1$到$v_n$称作格的基底，基底所包含的向量数成为格的维度。

当然，一个格中的向量可以互相转化。这个时候就需要用到转化矩阵，可以把一个格中的基底$V$转化成另一组基底$W$。那么我们就可以设置矩阵$T$，使得$W=TV$。当然，也有$V=T^{-1}W$。

不过这里就有个问题出现了：由于我们要求所有的$a$均为整数，那么我们就要保证$T,T^{-1}$中的每个元素都是整数。而满足这种条件下的$T$，必须满足$\det T=±1$。

比如，假设某个三维格的向量的基底是$\vec v_1=(5,4,-1),\vec v_2=(2,1,2),\vec v_3(3,4,-4)$。我们就可以通过一个$\det T=1$的矩阵$T$将其切换成另一基底,运用$W=TV$，我们可以得到基底向量组$W$,与$V$等价。其中$\vec w_1=(-2,17,11),\vec w_2=(7,11,14),\vec w_3=(-13,5,-7)$。其中系数矩阵$T$均为整数。同理，$V=T^{-1}W$中，由于$\det T=1$，因此$T,T^{-1}$中的每个数字也都是整数，符合格中向量的运算标准。

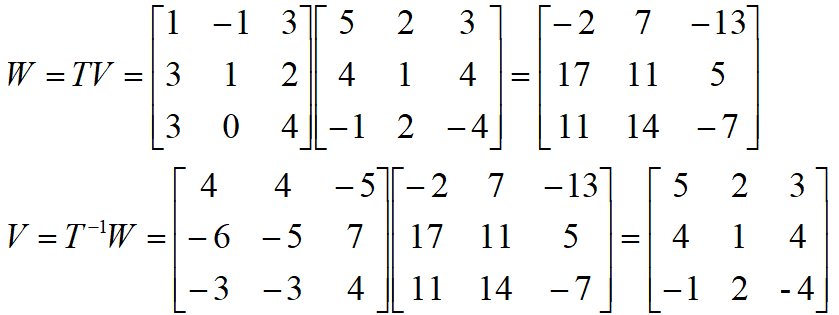
所以，格中的一组基底只需要写成矩阵的形式，并在其左边乘上一个行列式为$±1$的矩阵，就可以获得这个格的另一组基底。而这种矩阵的集合又称为线性群，用$\text{GL}_n(Z)$表示。这些矩阵每个元素都是整数，并且其逆矩阵的每个元素也都是整数。

对格的定义2：如果$R^m$的子集$L$在加减法下是封闭的，那么它是一个加性的子群。如果存在一个正常数$r$，使得$L$中的任意一个向量$\vec v$和$R^m$中的任意一个向量$\vec w$，都有$|\vec v - \vec w|<r$恒成立。

说的通俗易懂一些，就是我在$L$中取任意向量$\vec v$，然后在$\vec v$周围画一个半径为$r$的实心球（$2D$平面上则是一个圆），那么这个球里面没有$L$的其他点。

所以根据我们刚才的理论：格与向量空间相似，只不过它里面的所有的向量都是由各个基底与整数相乘得来的，所以格一般用点阵表示。比如，一个最简单的格就是
$$
L:\text{ } \vec v=(x,y)|x,y \in Z \text {}
$$
此时这个格就有一组基底为$\vec i =(1,0)$和$\vec j=(0,1)$，对应的就是二维坐标纸上的所有的整数点。

基本域F：指所有基底围成的空间，写成表达式就是$F(\vec v_1,\vec v_2,…,\vec v_n)=a_1\vec v_1+a_2 \vec v_2 +…+a_n \vec v_n$。其中$\vec v$是格中的基底向量，$a \in [0,1)$

例如，在我们刚才提到的最简单的那个格中，以$(0,0),(1,0),(0,1),(1,1)$四个点围成的正方形内部就是一个基本域，如下图中的灰色部分。

如果我们仍然是二维的格$P$，若该格$P$以$(1,2),(2,1)$为基底，那么基本域是由$(0,0),(1,2),(2,1),(3,3)$四点所围成的平行四边形。

假如$\vec t \in F,\vec v $是格$L$的一个基底，那么我们就可以得到其他的域$F+\vec v$，其中$\vec t$在域$F+\vec v$对应的向量是$\vec t + \vec v$

因此，这个可以覆盖整个$R^n$，当$n=2$时，我们还以上面那个最简单的二维格为例，就可以得到坐标纸上其他的域。比如$F+\vec i,F-\vec j,F+2\vec i +2 \vec j$

在坐标纸上，我们根据我们的发现，可以看到每个小正方形的面积都是$1$，扩展到$n$维空间，我们可以类比：所有的基本域的体积都是相等的，因此，基本域体积不变是格中一个非常重要的性质。并且$F$的$n$维体积又被成为$L$的行列式，记为$\det L$。继续用上面的例子，$\det L = 1,\det P = 3$。并且这里的$\det $值，刚好是对应的向量写成矩阵形式后，矩阵行列式的值的绝对值。

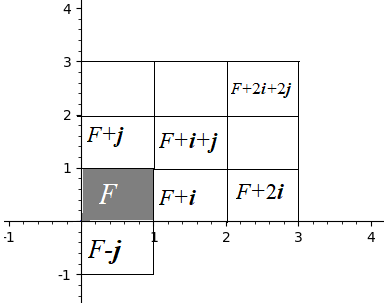
当然，这边还有一个推论： $\det L = \text{Vol } F≤|\vec v_1||\vec v_2|…|\vec v_n|$，也就是基本域$F$的面积小于等于所有基底的长度。并且基底越趋近于正交，那么不等号两边越靠近。

5.格中的短向量

5x01 两个问题：

最短向量问题SVP：在格$L$中寻找一个向量，使它的长度最小。

最接近向量问题CVP：给定一个$R^m$中的向量$\vec w$，要求在格中寻找一个向量$\vec v$，使得$\vec w-\vec v$的长度最小。

当然，SVP问题和CVP问题都可能有多个解，继续拿我们在第4节中所讲到的那个最简单的格的例子，格中的最短向量有$4$个，分别是$(0,1),(1,0),(0,-1),(-1,0)$。与$(0.5,0.5)$最接近的向量有$3$个，分别是$(0,1),(1,0),(1,1)$。而在笔记1中的2x04，2x05节，我们已经涉及到了相关的问题。只不过未能详细地讲解

这两个问题，也将随着格维度的提升，计算也会变得越来越困难。不过一般情况下，CVP问题难度略高于SVP难度，所以在维度更高的情况下，CVP问题可以转化成SVP问题来缩短解决问题的时间。但实际上，这两个问题也基本上可以说是在无 Trapdoor Infomation的情况下是无解的。因此我们可以寻找一些具有特殊性质的问题，比如我们在笔记1中提到过的背包密码问题。

当然，这两个问题还有很多变体，比如

最短基底问题SBP：在格$L$中寻找$n$个线性无关的向量作为基底，使得这些向量中最长的那个向量或者所有向量长度的平方和最小（这个问题有$2$个版本，因为不同情况下的要求是不同的）。

近似最短向量问题apprSVP：假设$f(n)$是$n$的函数，那么要求在维数为$n$的格内，找到一个非零向量，使其长度不超过$f(n)$倍的整个格中的最短非零向量。

当然，不同的$f(n)$会导致问题的不同，例如$f(n)=3n$或者$f(n)=5\ln^4 n$都会导致问题的不同。不过一般情况下，若$f(n)$是多项式，或

者格的位数较低，那么这个问题或许会更好解一点。

近似最接近向量问题apprCVP：类比于apprSVP问题。

5x02 Hermite’s theorem and Minkowski’s theorem

52o01 Hermite定理

我们在5x01中提到的问题，那么我们就得想一想了：最短的究竟有多长呢？下面说一下结论：格中最短向量的长度取决于格$L$的维数和行列式$\det L$的值。

(Hermite定理) 维数$n$的每一个格$L$都包含一个长度不超过$\sqrt n· \sqrt[n]{\det L}$的向量$\vec v$

(Hermite常数) 在给定维数下，每一个格$L$的最短非零向量$\vec v$的长度的平方都不超过$ y_n\sqrt[n]{\det^2 L} $。其中$y_2$到$y_8$和$y_{24}$的值是目前已知的。这些数字分别是$ \dfrac 4 3,2,4,8,\dfrac {64} 3,64,256,4 $。不过$y_n \in [\dfrac {n}{2 \pi e},\dfrac{n}{\pi e}]$

把这个定理扩展一下，有这样的结论：在维数为$n$的格$L$中，存在一组基底，使得这些基底中每个向量的长度的乘积不超过$\sqrt{n^n}·\det L$。这一是对我们之前结论”$\det L$不超过所有向量长度的乘积”这一定理的补充。

Hadamard比率：假设$\vec v_1,\vec v_2,…,\vec v_n$是格$L$的一基底$B$，那么Hadamard比率$H(B)$计算公式满足$H(B)=(\dfrac{\det L}{\prod_{i=1}^n |\vec v_i|})^{1/n}$。$H(B)$的值总是在$(0,1]$之间，并且这个值越接近$1$，就表示这一组基底中的向量越正交。

封闭球：在向量空间$R^n$中，任何与向量$\vec a$距离不超过$r$的空间的集合，称作向量$\vec a$的封闭球，记为$B_r(\vec a)$，表达式为$(x_1-a_1)^2+(x_2-a_2)^2+…+(x_n-a_n)^2 ≤ r^2$。其中$x_1$到$x_n$是坐标分量，$a_1$到$a_n$时向量$\vec a$的分量。

4个定义：当$S$是向量空间$R^n$的一个子集时，我们有如下定义：

Update 7.29 修改了2月份的逻辑错误表述

如果存在一个实数$r$ 使得$S$中所有的向量都包含在封闭球$B_r(\vec 0)$中。在二维平面上就是包含在圆$x^2+y^2=r^2$内。那么称$S$中向量的长度是有界的，

若$\vec a$在$S$中，$-\vec a$也在$S$中，并且$\vec a +(- \vec a)= \vec 0$，那么称$S$中向量时对称的，

如果$S$中有任意两点$A,B$则线段$AB$上的每一个点都在$S$中，那么称$S$是凸性的，

如果对于$S$中的一点$A$，任意取值$r>0$，$B_r(\vec {OA})$中都有属于$S$的点，则点$A$也在$S$中，那么称是封闭的，

52o02 Minkowski定理

（Minkowski定理）：设$L$是$R^n$中的一个格，$S$是$R^n$中的一个对称凸集，那么$S$的体积$\text{Vol }S> 2^n \det L$时，$S$中就包含一个非零格向量。如果$S$是封闭的，那么上面的不等式也可以取等号。

5x03 高斯启发式

53o01 伽马函数

伽马函数的定义域是$s>0$，表达式如下

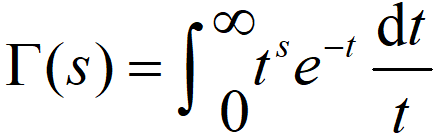
这个函数具有一些很重要的性质：

$\Gamma (1)=1,\Gamma(s+1)=s\Gamma(s)$。因此，当$s \in N_+$时，$\Gamma(s)=s!$

$\Gamma(\frac 1 2) = \sqrt \pi$

斯特林公式：$\lim _{s \to ∞} \Gamma(1+s)^{\frac1 s} =\dfrac s e$。更准确地说，应该是
$$
\lim _{s\to∞}\ln \Gamma (1+s)= \ln^s (\dfrac s e)+\dfrac 1 2 \ln (2 \pi s)+O(1)
$$

而这个伽马公式，在计算$n$维球体的体积中也就用到了：
$$
\text{Vol}(B_r(\vec a))=\dfrac{\pi^{\frac n 2}r^n}{\Gamma(1+\frac n 2)}
$$
当$n$较大的时候，这个$n$维球体的体积体积也近似于
$$
\text{Vol}(B_r(\vec a))^{\frac 1 n} ≈r\sqrt{\dfrac{2\pi e}{n}}
$$
又因为$\text{Vol}(B_r(\vec 0))≥2^n \det L$时，$B_r(0)$里面有非$0$格点。因此，当$n$较大的时候，球的半径的选取应该满足以下条件：
$$
r\sqrt{\dfrac{2\pi e}n}-2(\det L)^{\frac1n}= 0^+
$$
因此，当$n$很大的时候，$L$中也存在一个非零向量$\vec v$，满足
$$
|\vec v|-\sqrt{\dfrac{2n}{\pi e}}=0^-
$$
其中，有$\sqrt{\dfrac{2}{\pi e}}=0.484$

虽然在维数很大的时候，最段向量的长度是未知的，但是我们还是可以通过以下方法使用概率参数来估计它的大小：

在$r$很大的时候，$\text{Vol }{B_r(\vec 0)}$除以基本域$F$的体积$\text{Vol }F$ 近似等于$B_r(\vec 0)$中的格点数。

举个简单的例子，$x^2+y^2=r^2$中的整点数量约等于$\pi r^2$，也就是元的面积除以小正方形的面积$1$。

因此，我们很多情况下，都是想找到一个尽可能小的$r$值，使得球$B_r(\vec 0)$中至少有一个格点。，这就有了我们上面的估计表达式，移项，就有了
$$
r≈\sqrt{\dfrac{n}{2\pi e}}·\sqrt[n]{\det L}=\sigma (L)
$$
这就是我们得到的启发式，用$\sigma(L)$表示。

更准确地说，对于一个$c=0^+$的固定常数，那么对于一切维数为$n$的格$L$,都有
$$
|\vec v_{\text{shortest}}| \in[ \text{ }(1-c)\sigma(L),(1+c)\sigma(L) \text{ }]
$$
当$n$的数字较小时，对于$B_r(\vec 0)$的体积，估计式为
$$
\sigma(L)=\dfrac{(Γ((1+\frac{n}{2})·\det L))^\frac1n}{\sqrt \pi}
$$
通过SVP问题来类比CVP问题，可以推出：$\sigma (L)$的值也是$|\vec w - \vec v|$最小值的期望值。

就像SVP一样，如果$L$包含一个比$σ(L)$更接近$\vec w$的点，那么晶格约简算法就更容易求解CVP。

99.注

由于向量可以用坐标表示，因此此博客中，向量表示的也可以视为某个坐标，比如博客中最后一句话中的$\vec w$就是用向量的方法来表示某个点的坐标。