LatticeNotes4

huangx607087学习格密码的笔记4

0. About

一个密码学fw的学习笔记，别看，很菜的。

这个笔记接着之前发布的笔记3，继续往后面扩展新的内容。

10.NTRU公钥加密系统

10x00 Introduction

基于整数因式分解难度或离散对数问题的密码系统是基于群的密码系统，因为底层的硬问题只涉及一个操作。 对于RSA、Diffie-Hellman和ElGamal，该组是模量$m$的单位模$m$的组，它可能是素数或复合的，群运算是乘法模$m$。对于ECC，组是椭圆曲线模$p$上的点集，群运算是椭圆曲线加法。

环是具有加法和乘法两种运算的代数对象，它们是通过分配律连接起来的。 在这一部分中，我们描述了NTRU公钥密码系统。 使用卷积多项式环最自然地描述NTRU，但潜在的困难的数学问题也可以解释为晶格中的SVP或CVP。

10x01 NTRU公钥密码体制

固定一个整数$n≥1$和两个模数$p,q$并令$R,R_p,R_q$分别为卷积多项式环。（具体内容请回顾笔记3）

我们可以先将多项式$f(x)\in R$通过取模的方式降低其系数，使其成为$R_p$或者$R_q$中的元素，当然，我们也可以将$R_p$或者$R_q$中的元素看作是$R$中的元素。我们可以对参数$n,p,q$做出各种假设，特别地，我们可以要求$n$是素数，$\gcd (n,q)=\gcd(p,q)=1$等等。

在进入NTRU密码体制之前，我们要先引入一个符号：$T(d_1,d_2)$表示一类多项式的集合。若$f(x)\in T(d_1,d_2)$，就意味着$f(x)$中，有$d_1$个系数的值为$1$，有$d_2$个系数的值为$-1$，其他的系数的值均为$0$。例如：$f(x)=x^7-x^6+x^4+x^3-x+1\in T(4,2)$

$T(d_1,d_2)$中的多项式可以称为三元多项式，因为多项式中系数的取值范围只有$0$和$±1$。而我们以前说的二进制多项式中，由于多项式里只存在$0,1$两种系数，这又可以成为二元多项式。

下面我们进入这个密码系统：

首先，Alice确定四元整数组$(N,p,q,d)$。满足$N,p$均为素数，$\gcd(N,q)=\gcd (p,q)=1$，且$q>(6d+1)p$。

然后，Alice随机选取两个多项式$f(x)$和$g(x)$作为私钥，其中$f(x) \in T(d+1,d)$,$g(x)\in T(d,d)$，并计算$f(x)$在$R_p,R_q$中的逆$F_p(x),F_q(x)$。如果任意一个逆不存在，则重新选择$f(x)$。

然后，Alice在$R_q$中计算$h(x)=F_q(x)g(x)$和之前确定的四元数组作为公钥。

加密时，Bob的明文是$m(x)$，其系数均在$(-\dfrac12p,\dfrac12p]$内，也就是说，$m(x)$是$R$中的元素，同时也是$R_p$中的元素。然后再随机选取一个多项式$r(x)\in T(d,d)$并计算密文$c(x)\equiv ph(x)r(x)+m(x)\pmod q$，完成加密。

当Alice收到密文后，她计算$a(x)\equiv f(x)c(x) \pmod q$。

然后在$R_p$中计算$F_p(x)a(x)$，即可明文得到$m(x)$

下面我们来尝试一下这个密钥系统：

首先，Alice确定了整数$(N,p,q,d)=(7,3,41,2)$和$f(x)=x^6-x^4+x^3+x^2-1,g(x)=x^6+x^4-x^2-x$。保证了$f(x)\in T(3,2),g(x)\in T(2,2)$

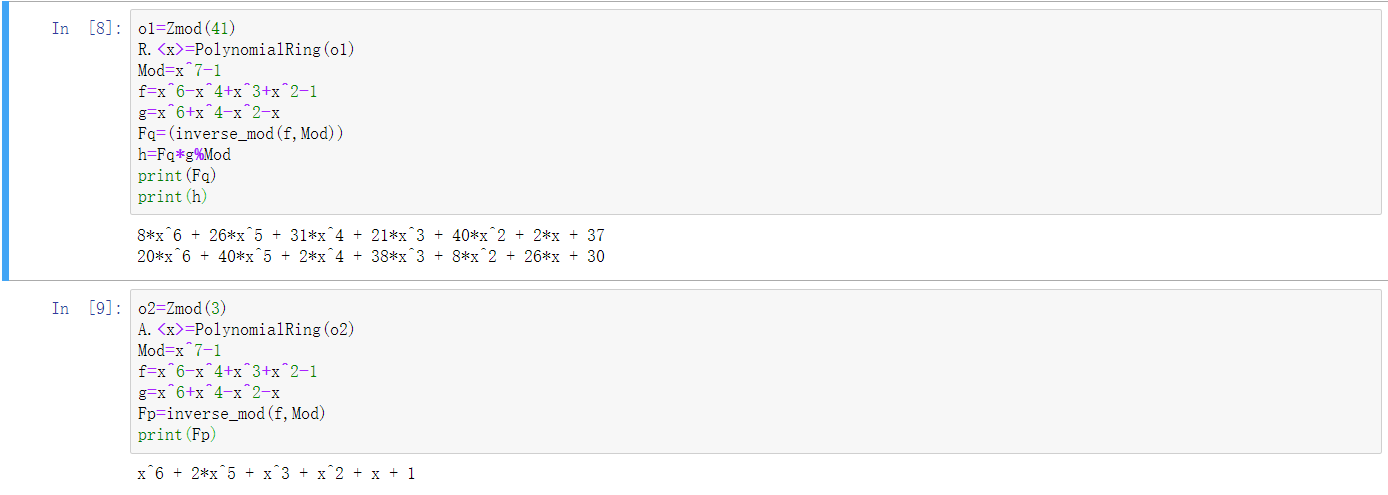
然后计算出了$F_p(x)=x^6+2x^5+x^3+x^2+1,F_q(x)=8x^6+26x^5+31x^4+21x^3+40x^2+2x+37$。

接着，Alice计算$h(x)=F_q(x)g(x)\equiv 20x^6+40x^5+2x^4+38x^3+8x^2+26x+30$。然后将$(N,p,q,d)$这一四元组和$h(x)$表达式公布作为公钥。

Bob选择了$R_p$中的表达式$m(x)=2x^5+x^3+x^2+2x+1$，将其调整为$m(x)=-x^5+x^3+x^2-x+1$。因为$p=3$，并且要保证$m(x)$中所有系数的绝对值不超过$p$一半，因此通过$2\equiv -1 \pmod3$来实现。

接着，Bob随机选择了一个在$T(2,2)$中的多项式$r(x)=x^6-x^5+x-1$

接着计算$c(x)=pr(x)h(x)+m(x)=31x^6+19x^5+4x^4+2x^3+40x^2+3x+25$，并将密文发送给Alice

Alice收到Bob的密文后，计算$a(x)=c(x)f(x)=x^6+10x^5+33x^4+40x^3+40x^2+x+40$。

在这里需要注意调整一下，由于$q=41$，因此我们将$a(x)$中所有的系数的绝对值调到不超过$20$，于是有了
$$
a(x)=x^6+10x^5-8x^4-x^3-x^2+x-1
$$
最后我们计算$F_p(x)a(x)=2x^5+x^3+x^2+2x+1$，调整系数后，得到$-x^5+x^3+x^2-x+1=m(x)$。因此获取明文。

这个加密算法中，最容易搞混的就是环在不断地换，不过归纳一下，发现只有$m(x)$的确定与解密的最后一步是用到$Zmod(p)$的，其他大多数时候用到的都是$Zmod(q)$。

10x02 NTRU中的数学问题

我们发现，$h(x)$的系数貌似是随机的，但经过验证，我们可以得出一个非常重要的结论
$$
f(x)h(x)\equiv g(x) \pmod {(x^N-1)} \text{ in } Zmod(q)
$$

并且$f(x),g(x)$的系数都是非常小的。因此假如已知$h(x)$的情况下，我们是否可以找到符合条件的$f(x)$和$g(x)$呢？

然而，这个解实际上并不唯一，因为如果$f(x),g(x)$满足上面那个等式，那么$x^kf(x),x^kg(x),k\in Z_N$也符合上面那个等式。此时我们解出来的答案就是$x^km(x)$。

更一般地，具有足够小系数和满足上面那个结论的任意对多项式$f(x),g(x)$作为NTRU解密密钥。 例如，如果$f(x)$是原始解密密钥，且$θ(x)$有微小的系数，那么$θ(X)f(X)$也可以作为解密密钥。

为什么人们会认为NTRU密钥恢复问题是一个困难的数学问题？ 第一个必要的要求是，这个问题实际上不能通过蛮力或碰撞搜索来解决。 我们将在后面的内容中讨论这样的搜索。 更重要的是，下面一节中，我们证明了求解NTRU密钥恢复问题（几乎肯定）等价于在某一类格中求解SVP。 这将NTRU问题与一个经过充分研究的问题联系起来，尽管这是一个特殊的晶格集合。 格约简的使用是目前最著名的从公钥恢复NTRU私钥的方法。 晶格还原是最好的方法吗？ 就像整数分解和其他密码系统背后的各种离散对数问题一样，没有人知道是否存在更快的算法。 因此，判断NTRU密钥恢复问题难度的唯一方法是注意，它已经被数学和密码社区很好地研究。 然后应用目前已知的最快算法，对求解问题的难度进行定量估计。

那么想要在没有密钥的情况下，破解NTRU系统又多难呢？

首先，就是$T(d_1,d_2)$中的多项式个数，一共有$\text C_N^{d_1}\text C_{N-d_1}^{d_2}$个符合条件的多项式。并且当$d_1,d_2$接近于$\dfrac N 3$的时候，$\text C_N^{d_1}\text C_{N-d_1}^{d_2}$的值时最大的。

对于蛮力搜索，攻击者必须尝试$T(d+1,d)$中的每个多项式，直到她找到一个解密键，但请注意，$f(x)$的所有循环移位都是解密键，因此有$N$个符合条件的选项。 因此，它将需要攻击者大约尝试$\dfrac {\text C_N^{d+1}\text C_{N-d-1}^{d}}{N}$，可以找到$f(x)$的一个循环移位)。

例如，如果一个符合条件的公钥为$(N,p,q,d)=(251,3,257,83)$。（注：这里的$q<(6d+1)p$，有可能出现解密失败）。那么想要找到一个可行的密钥，进行尝试的期望值$E$的数量级达到了$\ln E=\ln \dfrac{\text C_{251}^{84}\text C_{167}^{83}}{251}=264.5$。

当然，也可以使用空间换时间的做法，设定$f_1(x)=\sum_{i=1}^{(n/2)^-}$和$f_1(x)=\sum_{i=n/2}^{n}$。其中$(\frac n 2)^-$表示取不到$\frac n 2$。那么我们就可以找$f_1(x)h(x)$和$-f_2(x)h(x)$，看看是否有一样的内容（系数模$q$）。而这样的话，所需要的次数的数量级会降到$\ln E=132.3$，也就是指数降到原来的一半。而当$d$接近于$\dfrac N 3$的时候，这个算法的复杂度大概是$O(1.7321^N)$。

因此，这时解密成功的对数值约为$\ln P=\ln((\dfrac 3 {257})^{251}\text C_{251}^{84}\text C_{167}^{83})=-847$。若对数取$\log_2$，则值为$-1222$

故除了$f(x)$的循环移位之后的表达式外，有其他密钥的概率非常低。

11.NTRU与格密码系统

11x01 NTRU格

在这一部分中，我们解释了如何将NTRU密钥恢复表示为某一特殊类型晶格中的最短向量问题。

假设我们在某一次解出来的$N=3$情况下的$h(x)=39x^2+23x+48$，对应的$q$值为$61$，那么我们可以构造这样一个矩阵，其中空白部分均为$0$，大小是$6\text{x}6$

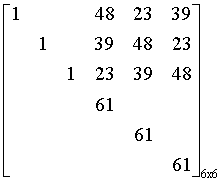
扩展到$n$阶，则是一个$2n$阶的矩阵

其中左上角是单位阵$E$，左下角是$0$矩阵，右下角是数量矩阵$qE$，右上角则是$h(x)$的各个系数循环得来的。

假如我们现在有
$$
f(x)=\sum_{i=0}^{N-1} a_ix^i \text{ and }g(x)=\sum_{i=0}^{N-1} b_ix^i
$$
然后我们可以构建一个向量$(\vec a,\vec b)=(a_0,a_1,…,a_{N-1},b_0,b_1,…b_{N-1})$。这个向量也是$2n$维的，因此可以右乘$M_{\text h}^{\text{NTRU}}$

我们现在假设NTRU公钥$h(x)$是使用私有多项式$f(x)$和$g(x)$创建的，并计算当我们将NTRU矩阵乘以一个精心选择的向量时会发生什么。

因为我们刚才提到过一个式子：$f(x)h(x)\equiv g(x)\pmod{x^N-1} \text{ in } R_q$。

那么我们可以写出这样的式子，其中$u(x)$也是一个多项式
$$
f(x)h(x)=g(x)+qu(x)
$$
因此，我们可以有
$$
(\vec f,-\vec {u})M_{\text h}^{\text{NTRU}}=(\vec f,\vec f·\vec h-q\vec u)=(\vec f,\vec g)
$$
因此，$(\vec f,\vec g)$在格$L_{\text h}^{\text{NTRU}}$中。

当公钥中的$d≈\dfrac N 3,q≈6d≈2N$时。则$\det L_{\text h}^{\text{NTRU}}=q^N $，$|(\vec f,\vec g)|≈2\sqrt d$。且由高斯启发式可以推出，最短非$0$向量的长度约为$\sigma(L_{\text h}^{\text{NTRU}})≈\dfrac{Nq}{\pi e}≈0.484N$。

当然，当$N$很大的时候，很大概率上，格中最短非零向量就是$(\vec f,\vec g)$或者其循环移位（又称旋转）。并且
$$
\dfrac {|(\vec f,\vec g)|}{\sigma (L)}≈\dfrac{2.39}{\sqrt N}
$$
所以$(\vec f,\vec g)$的长度数量级是$O(N^{-\frac 1 2})$，比高斯启发式所预测的长度要短。

11x02 对NTRU晶格的安全性的定量分析

由我们之前的分析，可以得出：如果攻击者能够在NTRU格中找到一个最短的向量，那么解决这个问题的难度就至少达到了SVP问题的求解，如果攻击者可以在格中解决apprSVP问题在不超过$O(\sqrt N)$的短向量，那么攻击者发现的短向量就很可能是解密密钥。因此，这里就涉及到了如何估计在NTRU格综合你找到一个给短的或者最短的向量难度的问题。因此我们在下一条笔记中会讲到有多项式时间复杂度的LLL算法，但$N$很大时，LLL算法是找不到很小的向量的，因此笔记5我们还会讨论讨论BKZ-LLL算法。不过其运行时间有可能会达到指数级别。

不幸的是，标准晶格约简算法(如BKZ-LLL)的操作特性并没有像素数筛算法、指数微积分胡总和Pollard Rho算法那么得到较好的理解。这使得理论上很难预测晶格约简算法在任何给定的类格上的性能。 因此，在实践中，必须通过实验确定基于晶格的密码体制(如NTRU)的安全性。

粗略地说，一个参数序列$(N,q,d)$，其中$N$增长，使涉及$N,q,d$的某些比率保持近似恒定。 对于每组参数，一个人使用BKZ-LLL进行了许多实验，随着块大小的增加$β$直到算法在$L^{NTRU}_h$中找到一个短向量。 然后绘制平均运行时间对N的对数，验证点近似在线，并计算最佳拟合线$\ln(\text{Running Time}=Ax+B)$。

在对N的许多值进行这样做之后，直到计算变得不可行时，人们可以使用这条线来推断NTRU晶格$L^{NTRU}_h$中寻找私钥向量所需的预期时间，以获得$N$的较大值。这些实验表明，$N$的值在$250$到$1000$之间，产生的安全与RSA、ElGamal和ECC目前的安全实现相当

刚刚我们说过，NTRU晶格中的短目标向量比高斯启发式预测的短$O( \sqrt N)$。 理论上和实验上，如果维数$n$的晶格具有极小的向量，例如$O(2^n)$比高斯预测短，那么LLL及其变体等晶格约简算法非常擅长于找到微小向量。 这是一个自然和非常有趣的问题，问是否只有$O(n^k)$比高斯预测短的向量也可能更容易找到。 这时，没有人知道这个问题的答案。